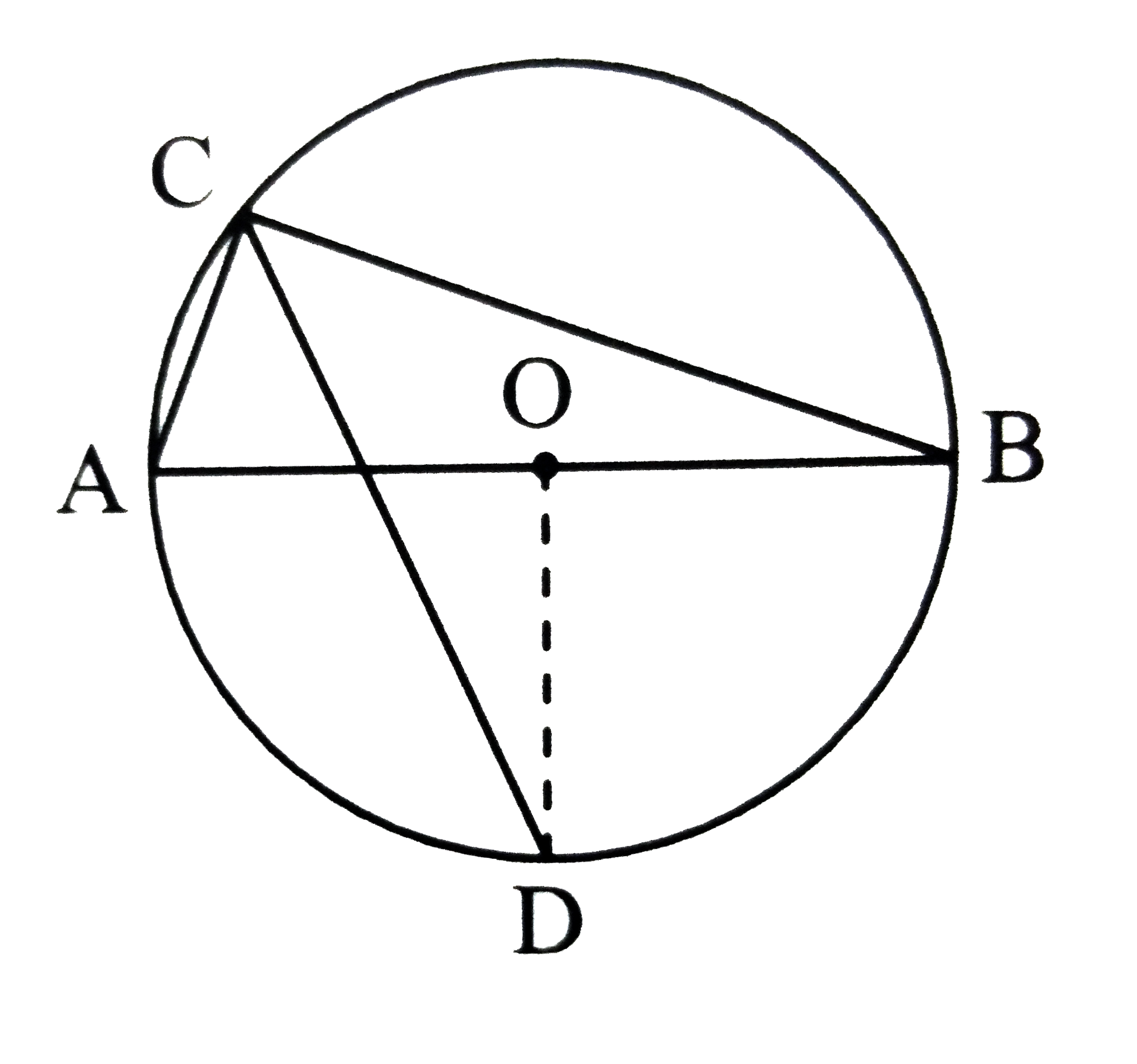
In figure, seg AB is a diameter of a circle with centre O. The bisector of intersects the circle at point D. Prove that seg AD seg BD. Complete the following proof by filling in the blanks

The correct Answer is: seg AD seg BD
Step by step video & image solution for In figure, seg AB is a diameter of a circle with centre O. The bisector of /_ACB intersects the circle at point D. Prove that seg AD cong seg BD. Complete the following proof by filling in the blanks by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.56videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
In the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
 View Solution
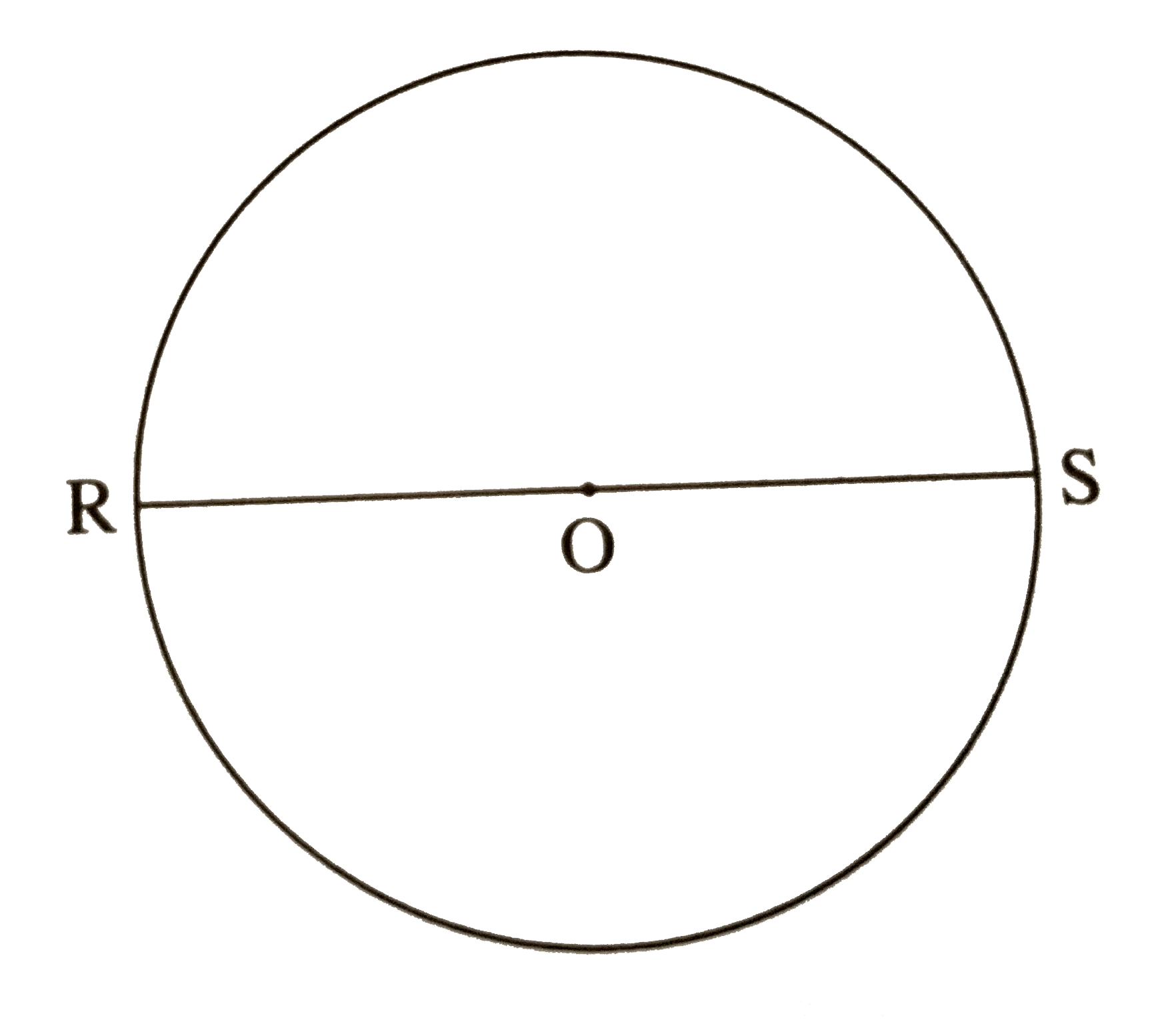
View SolutionIn figure, seg RS is a diameter of the circle with centre O. Point T lines in the exterior of the circle. Prove that ∠RTS is an acute angle.
 View Solution
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
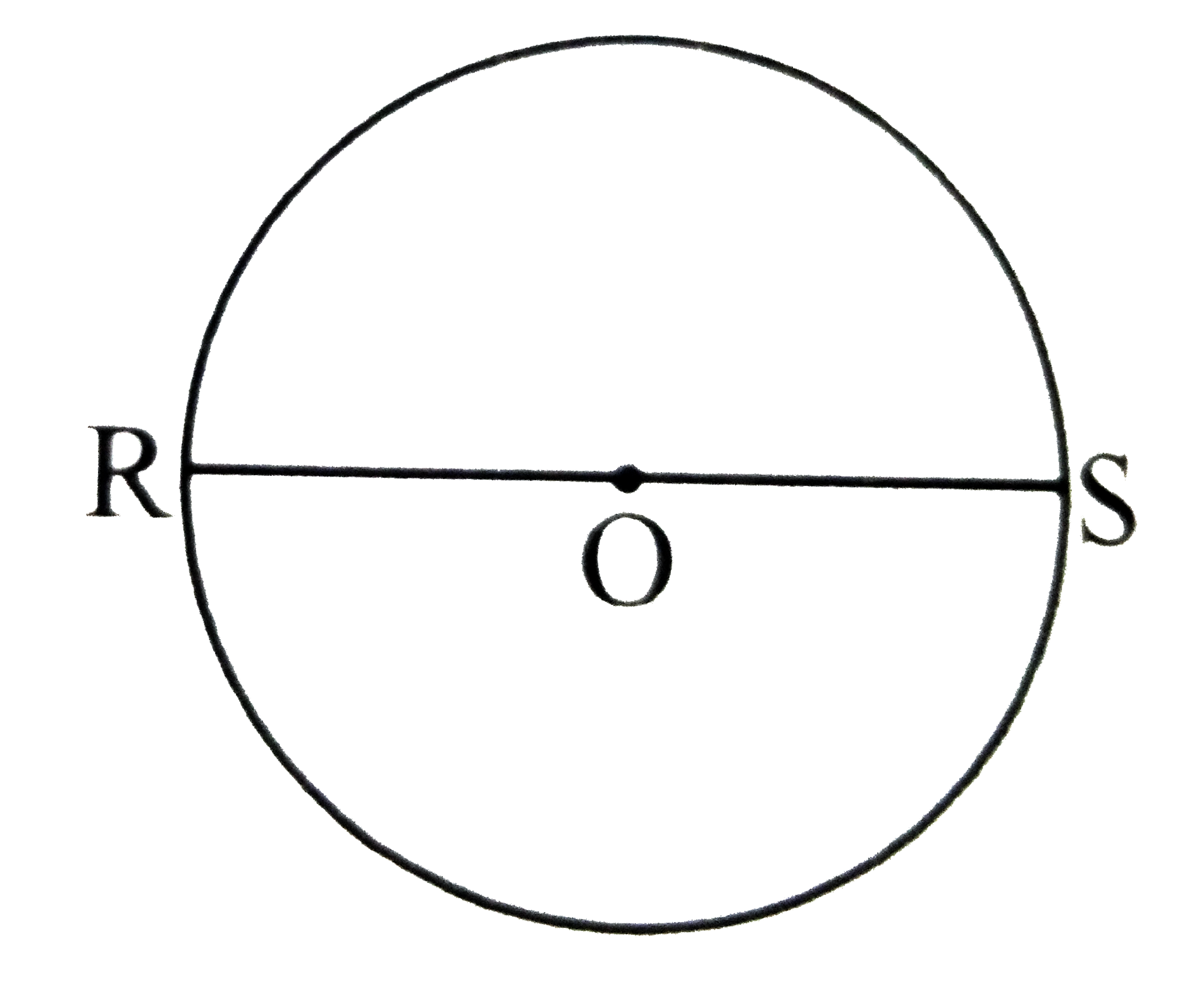
View SolutionIn the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
 View Solution
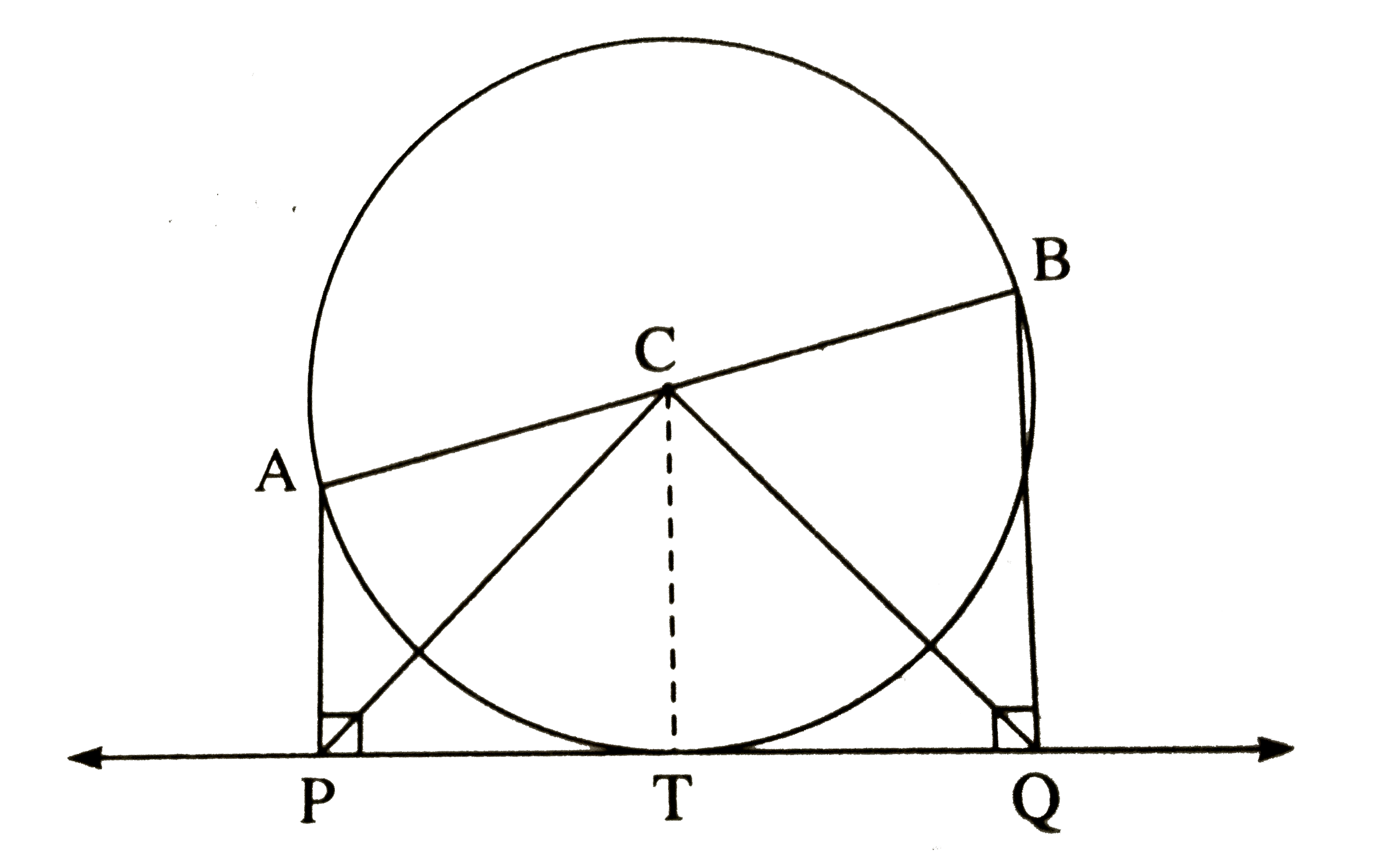
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
 View Solution
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.
 View Solution
View Solution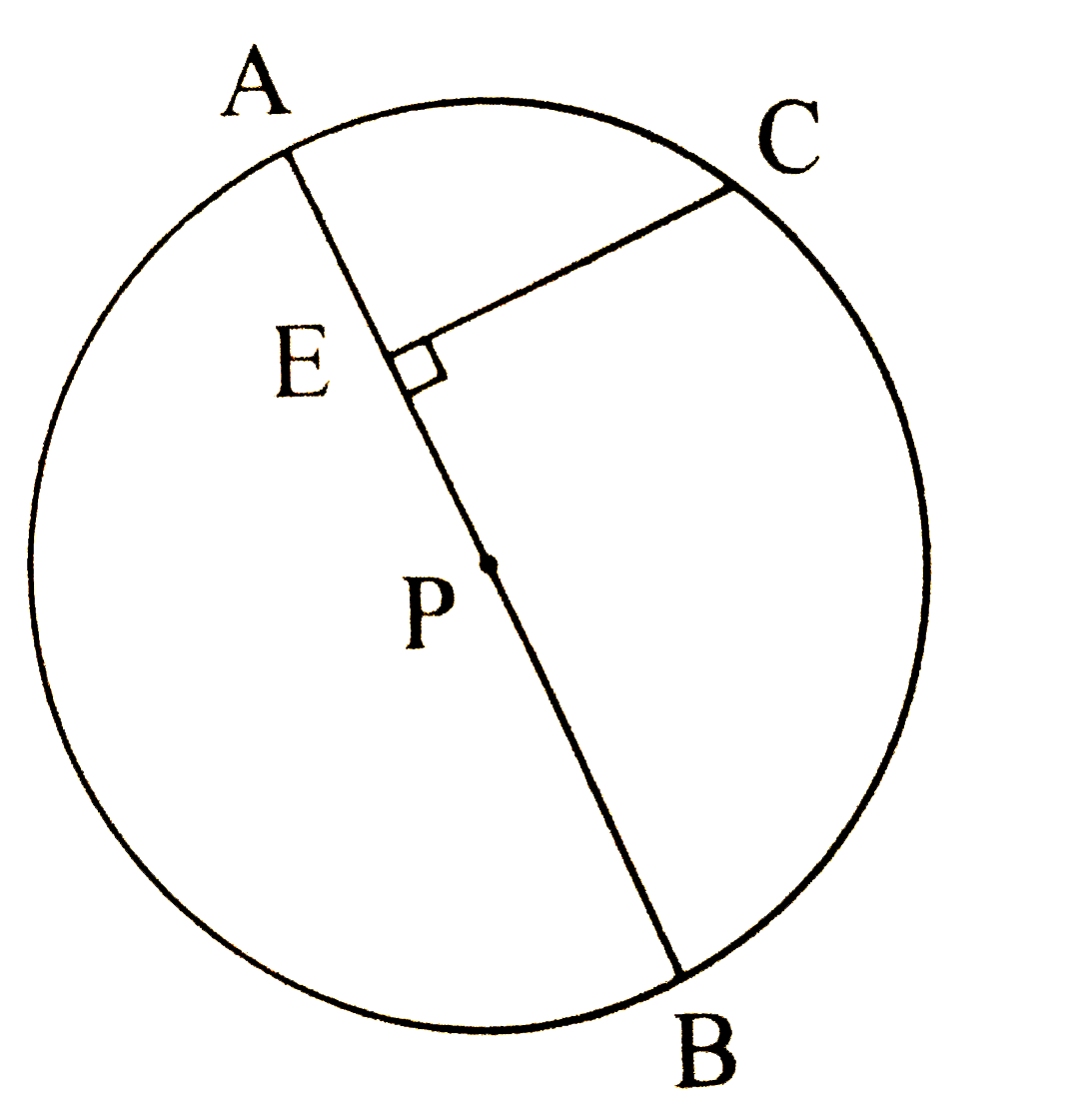
In the above figure, seg AB is a diameter of a circle with centre P.C is any point on the circle. Seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of folloing steps:
(a) Draw ray CE. It intersects the circle at D.
(b) Show that CE = ED.
Write the result using theorem of intersection of chords insides a circle.
(d) Using CE = ED, complete the proof.View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
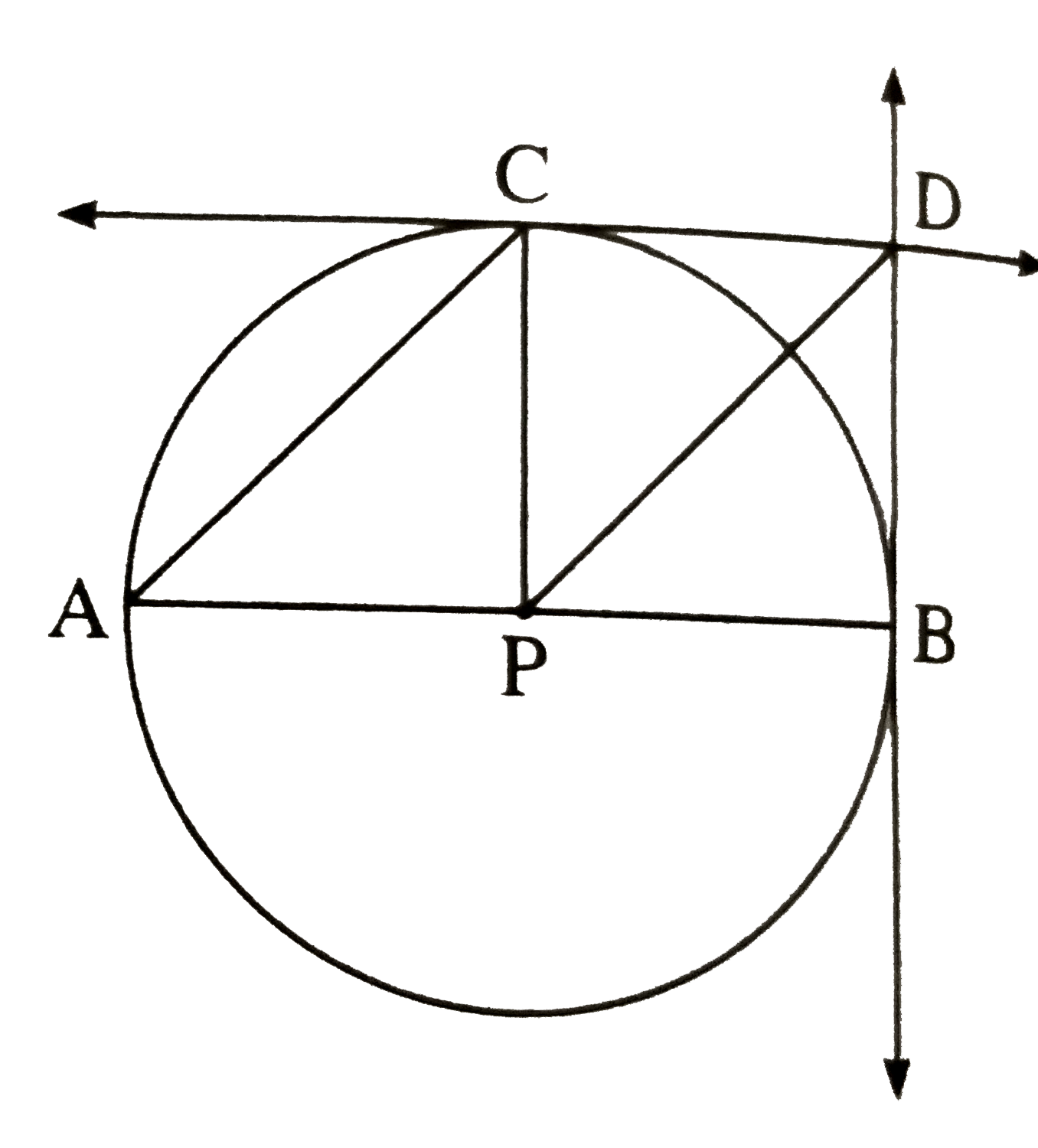 View Solution
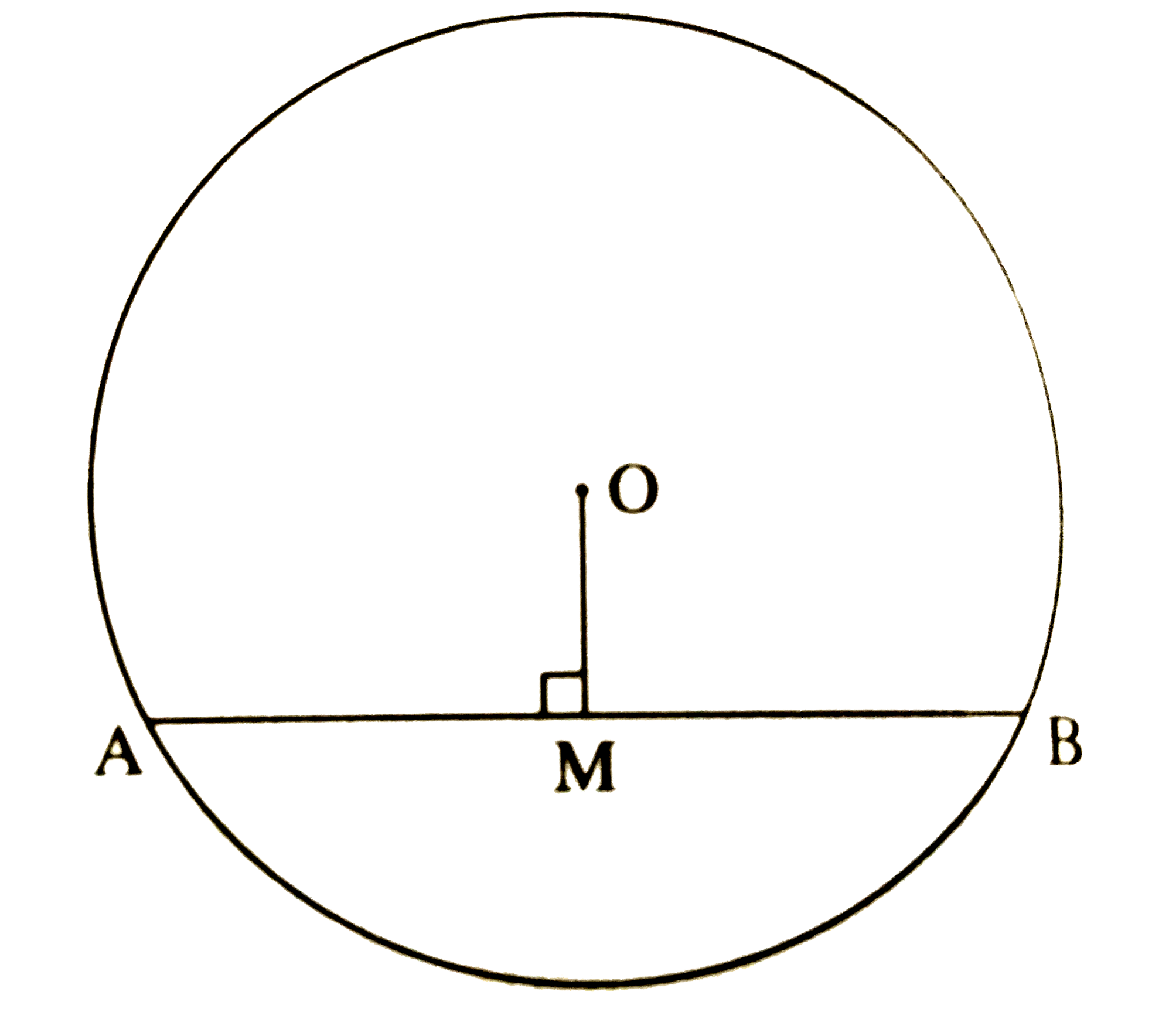
View SolutionIn the figure , seg AB is the chord of the circle with centre O. if AM =4 cm then find MB and AB. State your reason.
 View Solution
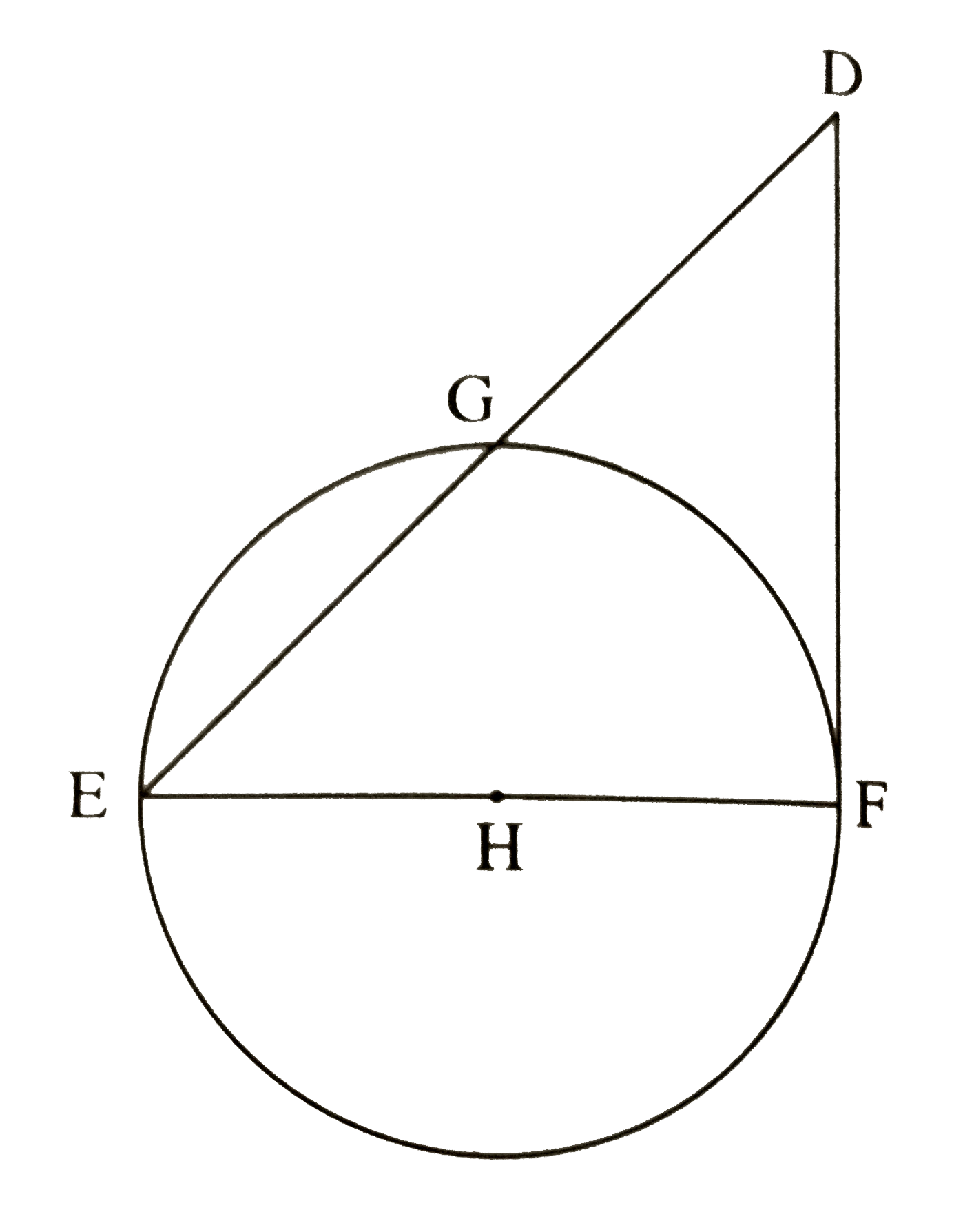
View SolutionIn figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
 View Solution
View Solution

