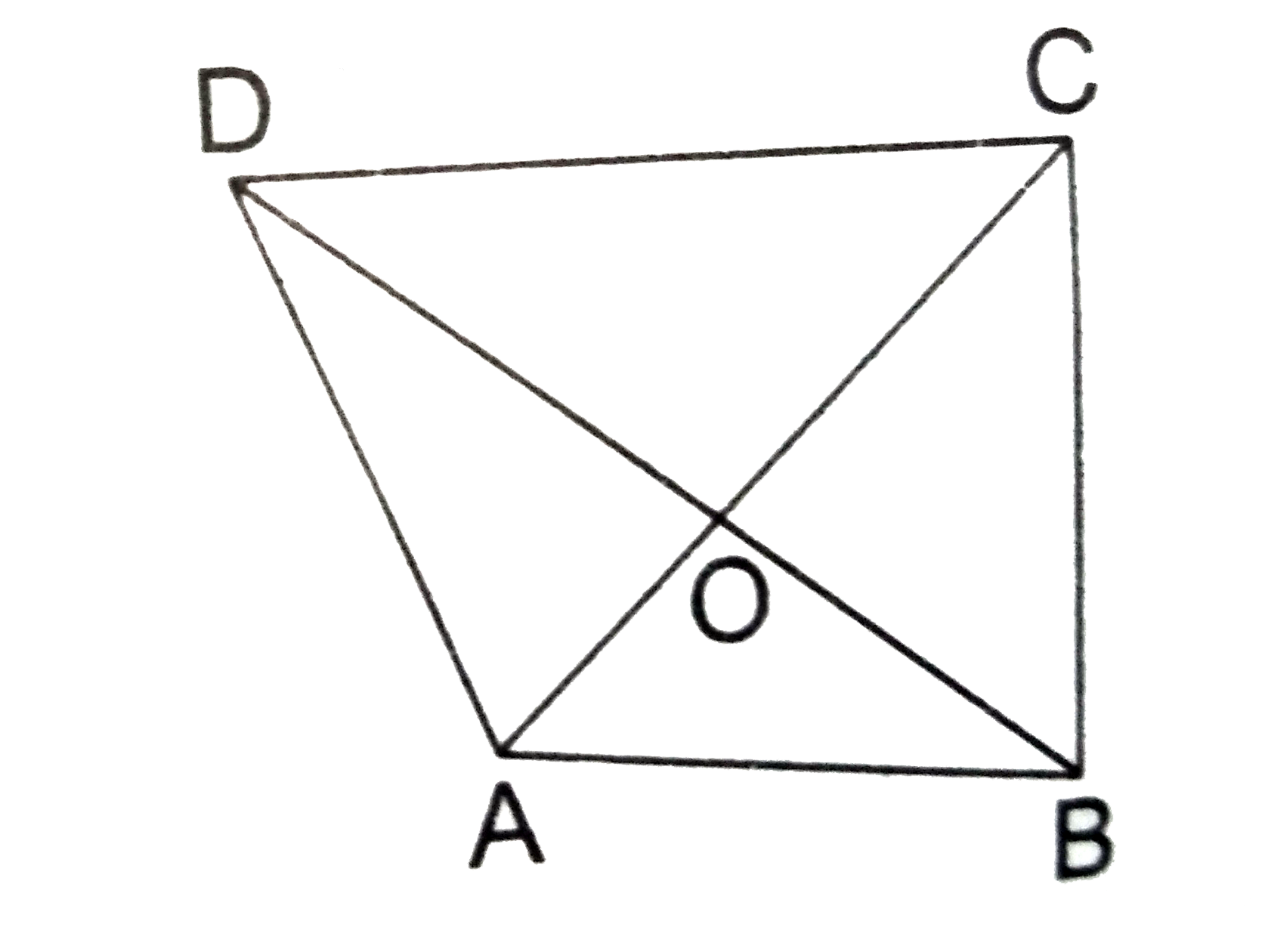
In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar(ΔDOC) = ar(ΔAOB)
Step by step video & image solution for In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that ar(DeltaDOC) = ar(DeltaAOB) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.4)
19 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Multiple Choice Questions )
45 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.2)
7 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
In the figur e, diagonals AC and BD of quadrilateral A BCD intersect at 0 such that OB = OD. If AB = CD, then show that

ar(ΔDCB) = ar(ΔACB)
View SolutionIn Fig 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.If AB=CD , then show that
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that

DA I I CB or ABCD is a parallelogram.
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
View SolutionDiagonal PR and QS of quadrilateral PQRS intersects at T such that PT= TR and PS= QR, show that ar (ΔPTS)= ar (ΔRTQ)
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionThe diagonals of quadrilateral ABCD, AC and BD intersects at O. Prove that if BO = OD then the triangles ABC and ADC are equal in area.
View Solution
