In the given figure, AB is a diameter of a circle C(O,r) and chord CD = radius OC. If AC and BD when produced meet at P, prove that ∠APB is constant.
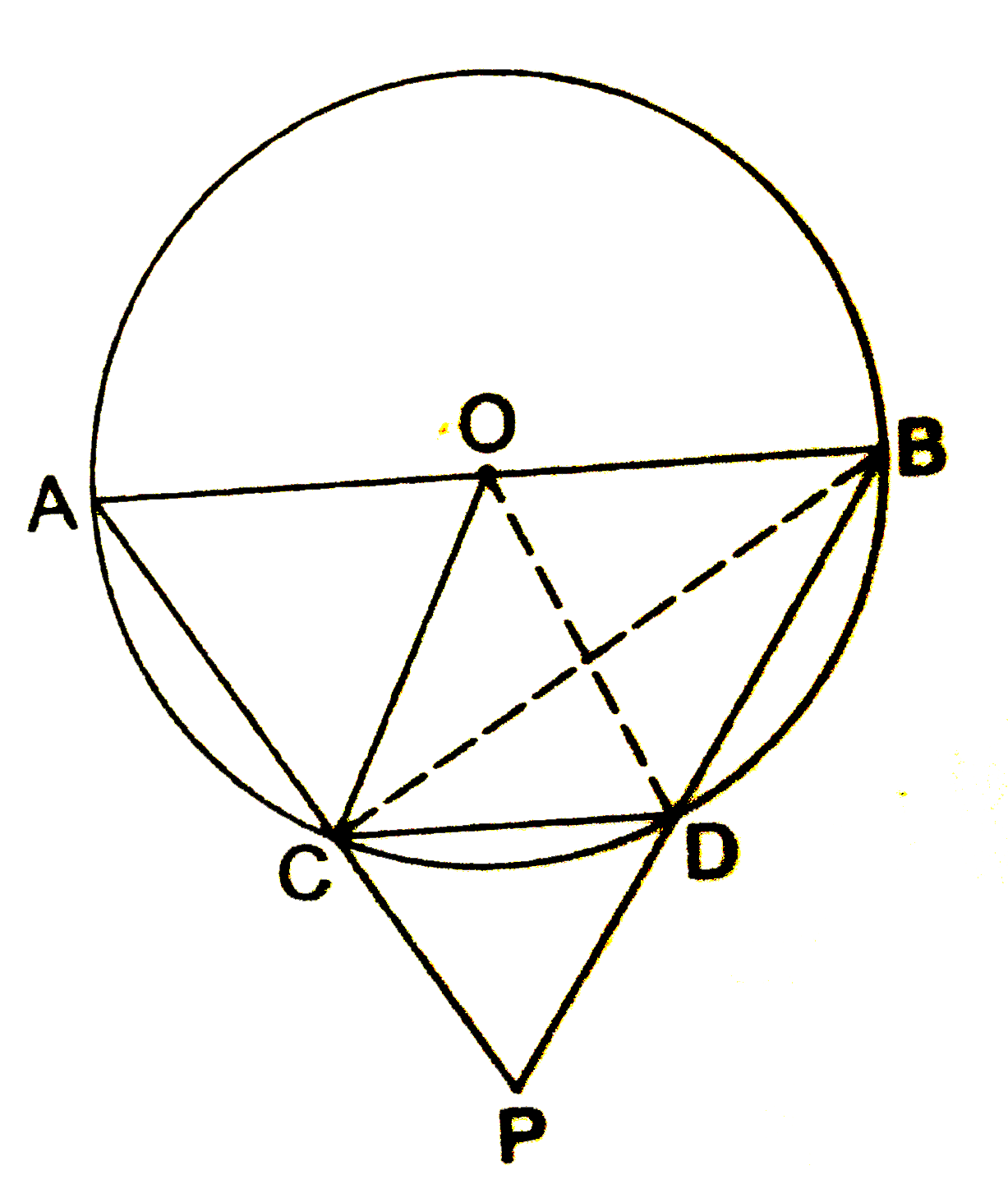
Video Solution
Text Solution
Join OD and BC.
Now, CD=OC=OD [ each equal to r ]
⇒ΔOCD is equilateral
⇒∠COD=60∘ ….(i)
Also, ∠ACB=90∘ [angle in a semicircle ] …..(ii)
And, ∠CBD=12×∠COD=(12×60∘)=30∘ ....(iii)
[∵ angle made by ˆCD at the centre
=2× angle at any point on its remaining part ] .
Now , side PC of ΔBPC is produced to A.
∴exterior angle = sumof interior opposite angles.
⇒∠ACB=∠APB+∠CBD
⇒90∘=∠APB+30∘ [ using (ii) and (iii) ]
⇒∠APB=60∘= constant.
Hence, ∠APBis constant.
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
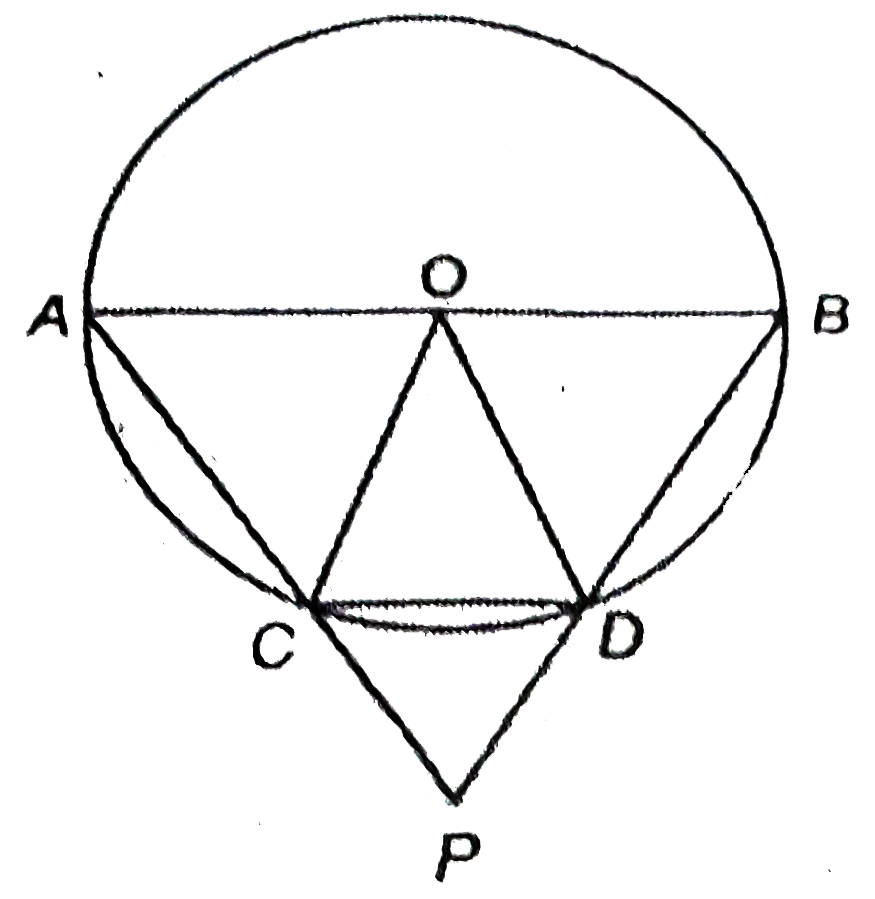
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
 A60∘B30∘C90∘D160∘
A60∘B30∘C90∘D160∘AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
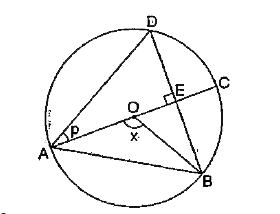 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−x
In the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn the given figure, if AC = BD, then prove that AB = CD.

View SolutionIn the given figure, AB∣∣CD. Prove that p+q−r=180.

View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View SolutionAB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
View Solution