In Figure, AB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
Step by step video & image solution for In Figure, A B is a diameter of a circle C(O ,\ r)dot Chord C D is equal to radius O Cdot If A C\ a n d\ B D when produced intersect at P , prove that /_A P B is constant. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, AB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionAB is a diameter of a circle. CD is a.chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E and AE=K.AB, then K is equal to
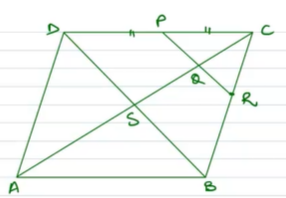
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
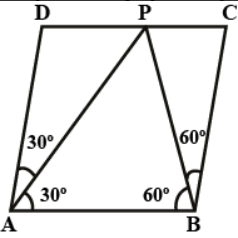
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View SolutionIn Figure, BE⊥AC, AD is any line from A → BC intersecting BE in H.P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR=900
View Solution
