In the given figure, ABCD is a parallelogram. The circle through A,B,C intersects CD produced at E. Prove that AD = AE
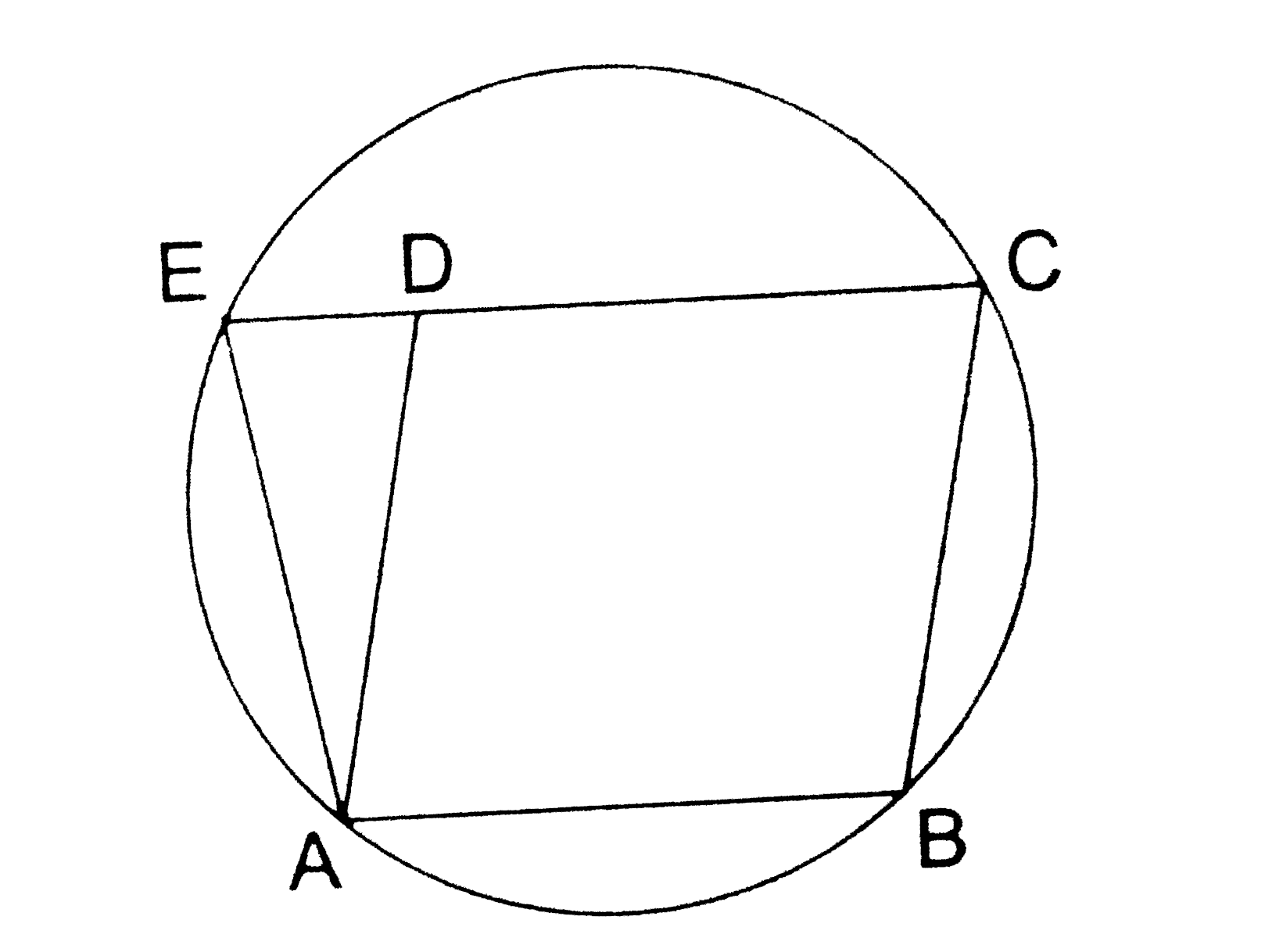
It is given that ABCE is a cyclic quadrilateral.
∴∠ABC+∠AED=180∘ .....(i)
Also, EDC is a straight line.
∴∠ADE+∠ADC=180∘
But,∠ADC=∠ABC [ opposite ∠s of a ∣∣ gm ]
∴∠ADE+∠ABC=180∘ ...(ii)
Thus,∠ABC+∠AED=∠ADE+∠ABC [ from (i) and (ii) ]
⇒/AED=∠ADE
⇒AD=AE [ opposite sides of equal of ∠s of Δ ADE ]
Hence, AD=AE.
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
ABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced ifnecessary) at E. Prove that AE = AD.
View SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.

View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View Solution
