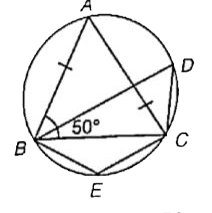
In the given figure, is isosceles with and . Find and .

Video Solution
Text Solution
But,
in the same segment ].
Now, BECD being a cyclic quadrilateral, we have
Hence, and .
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, ABC is an isosceles triangle in which AB=ACand∠ABC=50∘,∠BDC :
 A80∘B60∘C65∘D100∘
A80∘B60∘C65∘D100∘In the given figure, △ABC is an isosceles triangle in which AB=AC and ∠ABC=50∘ , the ∠BDC is equal to
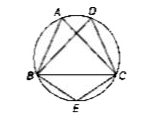 A60∘B10∘C80∘D90∘
A60∘B10∘C80∘D90∘
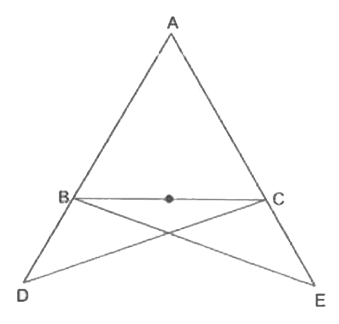
In the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
View SolutionIn ΔABC,∠A=1000 and AB=AC. Find ∠B and ∠C
View SolutionIn ΔABC,AC=BC and ∠BAC=70∘. Find ∠BCA
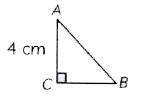
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
View SolutionIf △ABC is an isosceles triangle with AB = AC and ∠ABC is 65∘, then ∠BCA and ∠BAC are, respectively
यदि △ABC, AB = AC और ∠ABC=65∘ के साथ एक समद्विबाहु त्रिभुज है, तो क्रमशः ∠BCA और ∠BAC है:
View SolutionIn the figure, ABC is an isosceles triangle in which AB = AC and LM is parallel to BC. If ∠A=50∘ find ∠LMC.
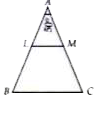
View Solution
