In the given figure , two equal chord AB and CD of a circle C(O,r) when produced meet at a point E.
Prove that (i)BD=DE
(ii)AE=CE
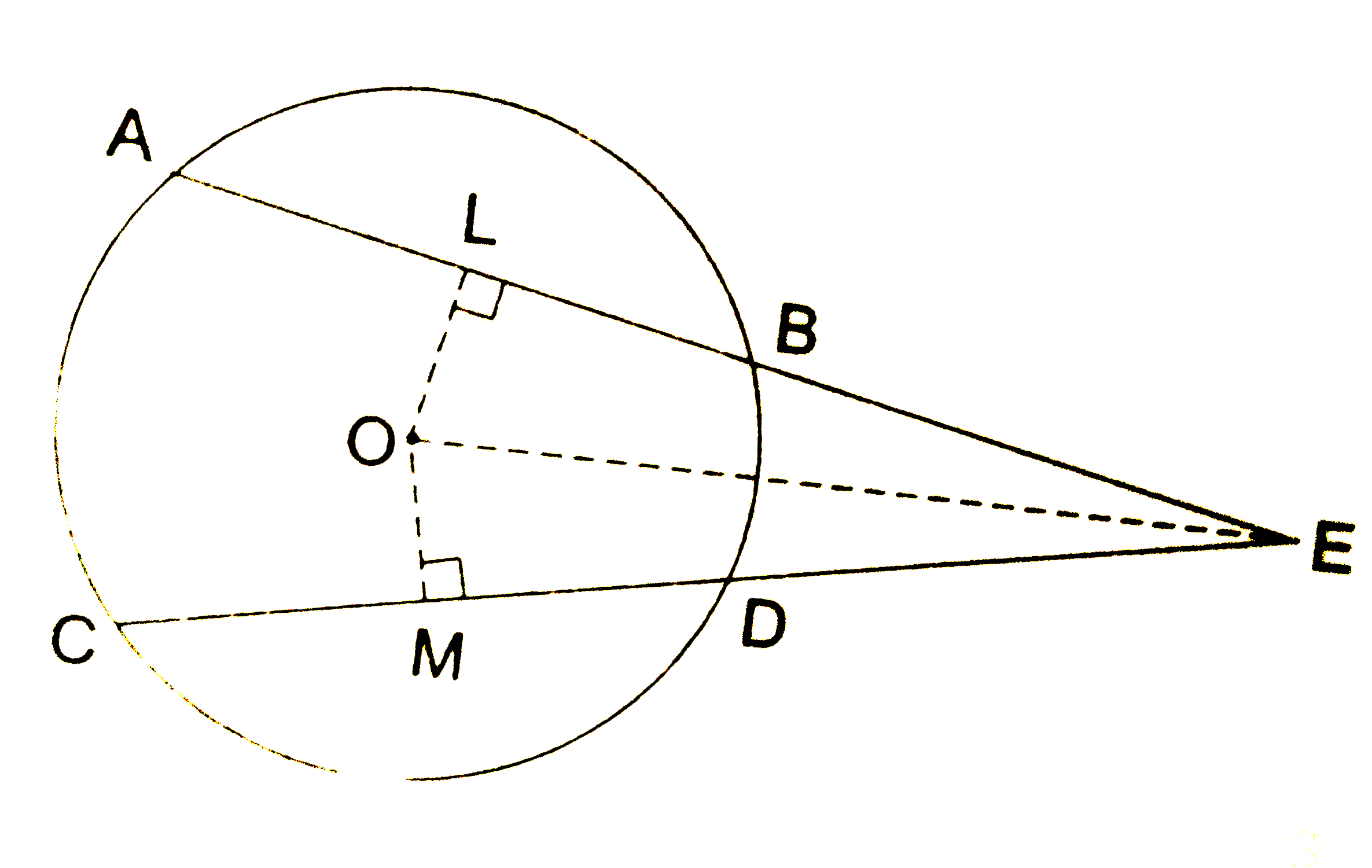
Join OE.
Draw OL ⊥ AB and OM ⊥ CD.
We know that equal chords of a circle are equidistant from the centre.
∴OL=OM.
In the right ΔOLE and OME, we have
OL = OM
OE=OE [common]
∴ΔOLE≅ΔOME [ by RHS - congruence ]
⇒LE=ME .....(i) [c.p.c.t.].
Also, AB=CD⇒12AB=12CD
⇒BL=DM ....(ii)
On subracting (ii) from (i), we get
LE−BL=ME−DM⇒BE=DE. [Part (i) proved]
Now, AB=CD and BE= DE
⇒AB+BE=CD+DE
⇒AE=C,
Hence, BE=DE and AE=CE.
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
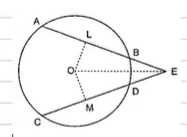
Two equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure, Prove that BE=DE and AE=CE.
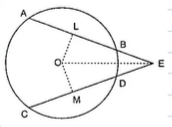
View SolutionTwo equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View SolutionIn the given figure if AC=BD then prove that AB=CD
View SolutionABandCD are equal chords of a circle whose centre is O, when produced these chords meet at E,Prove that EB=ED.
View SolutionIn the given figure, if AC = BD, then prove that AB = CD.

View SolutionABCD is cyclic quadrilateral in which AB and CD when produced meet in E and EA = ED. Prove that (i) AD || BC (ii) EB=EC
View SolutionIn the given figure, two chords AC and BD of a circle intersect at E.If arcAB=arcCD, prove that : BE=EC and AE=ED
View SolutionL and M are mid-point of two equal chords AB and CD of a circle with centre O . Prove that ∠OLM= ∠OML (ii) ∠ALM= ∠CML
View Solution
