In trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that $\frac{B E}{E C} = \frac{3}{4}$ .
Diagonal DB intersects EF at G. prove that &EF= 10AB.

Video Solution

Text Solution

Verified by Experts

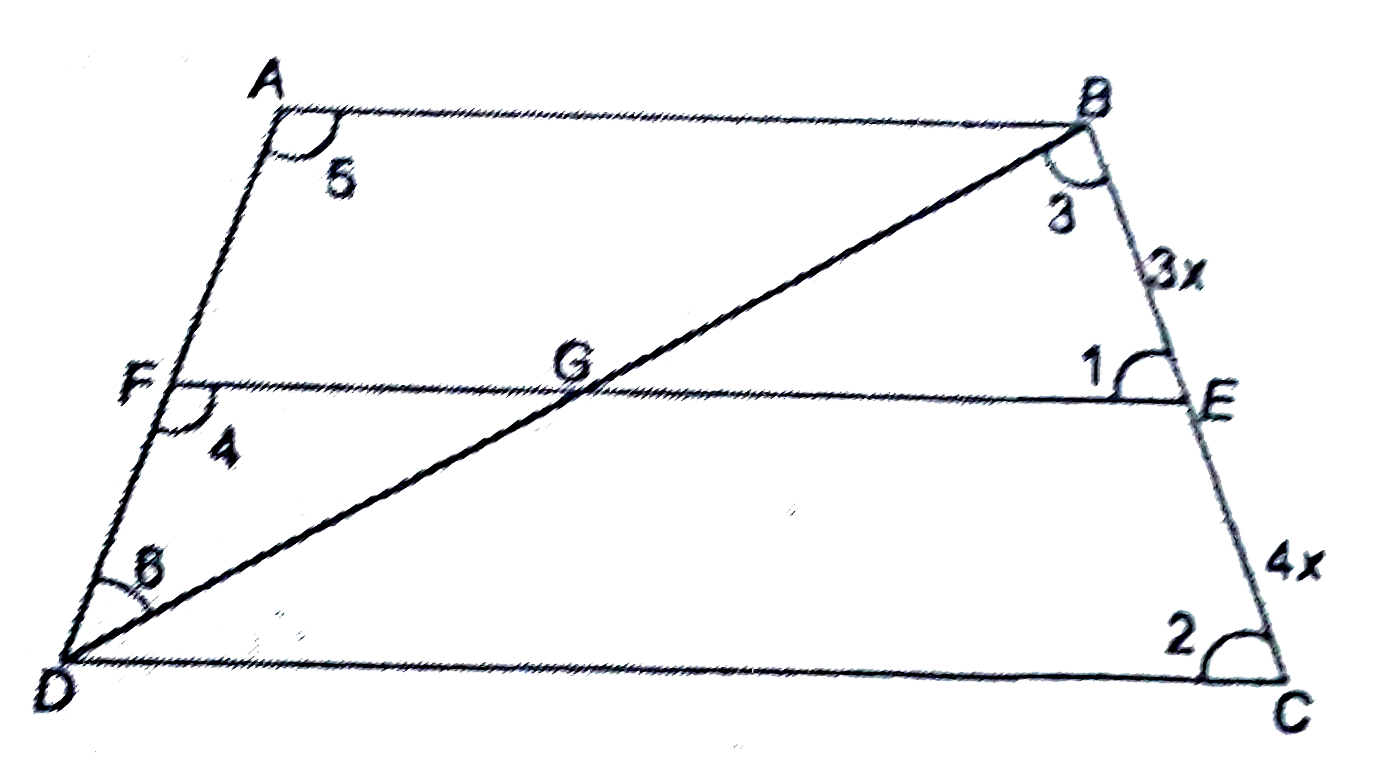
Since GE||DC
$\frac{B E}{E C} = \frac{B G}{G D}$ (by B.P theorem ) …(1)
Also GF||AB
$\frac{A F}{F D} = \frac{B G}{G D}$ (by B.P theorem) ….(2)
from (1) and (2) , we get
$\frac{A F}{F D} = \frac{B E}{E C} = \frac{3}{4}$
In $△ B G E and △ B D C$
$∠ 1 = ∠ 2$ (corresponding $∠ s$ as GE||DC)
$∠ 3 = ∠ 3$ (common)
$△ B G E ~ △ B D C$ (AA corocllary)
$\frac{G E}{D C} = \frac{B E}{B C}$ (corresponding sides of similar triangles are proportional)
$\frac{G E}{2 A B} = \frac{3}{7} (D C = 2 A B)$
$\Rightarrow \frac{G E}{A B} = \frac{6}{7}$ ....(4)
Now in $△ D F G and △ D A B$
$∠ 4 = ∠ 5$ ( corresponding $∠ s$ as FG||AB)
$∠ 6 = ∠ 6$ (common)
$△ D F G ~ △ D A B$ (AA corollary)
$\frac{F G}{A B} = \frac{D F}{D A}$
$\Rightarrow \frac{F G}{A B} \frac{4}{7}$ ( from 3)...(5))
Adding (4) and (5) , we get
$\frac{G E}{A B} + \frac{G F}{A B} = \frac{6}{7} + \frac{4}{7}$
$\frac{G E + G F}{A B} = \frac{10}{7}$
$\frac{E F}{A B} = \frac{10}{7}$
$\Rightarrow 7 E F = 10 A B$ Hence proved.

Updated on:21/07/2023