InΔPQR≅ΔEFD, Which side ofΔPQR equals ED? Which angle ofΔPQR equals ∠E?
To solve the question, we need to identify the corresponding sides and angles of the two congruent triangles, ΔPQR and ΔEFD.
1. Identify the Congruent Triangles:
We are given that ΔPQR is congruent to ΔEFD. This means that all corresponding sides and angles of these triangles are equal.
2. Corresponding Sides:
- In congruent triangles, the corresponding sides are equal.
- The sides of ΔPQR correspond to the sides of ΔEFD as follows:
- PQ corresponds to EF
- QR corresponds to FD
- PR corresponds to ED
3. Determine which side of ΔPQR equals ED:
- From the correspondence established, we see that PR (side of ΔPQR) corresponds to ED (side of ΔEFD).
- Therefore, PR = ED.
4. Corresponding Angles:
- Similarly, we can identify the corresponding angles:
- Angle P corresponds to angle E
- Angle Q corresponds to angle F
- Angle R corresponds to angle D
5. Determine which angle of ΔPQR equals angle E:
- From the correspondence of angles, we find that angle P = angle E.
Final Answers:
- The side of ΔPQR that equals ED is PR.
- The angle of ΔPQR that equals angle E is angle P.
We are given that ΔPQR is congruent to ΔEFD. This means that all corresponding sides and angles of these triangles are equal.
- In congruent triangles, the corresponding sides are equal.
- The sides of ΔPQR correspond to the sides of ΔEFD as follows:
- PQ corresponds to EF
- QR corresponds to FD
- PR corresponds to ED
- From the correspondence established, we see that PR (side of ΔPQR) corresponds to ED (side of ΔEFD).
- Therefore, PR = ED.
- Similarly, we can identify the corresponding angles:
- Angle P corresponds to angle E
- Angle Q corresponds to angle F
- Angle R corresponds to angle D
- From the correspondence of angles, we find that angle P = angle E.
- The side of ΔPQR that equals ED is PR.
- The angle of ΔPQR that equals angle E is angle P.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If p is the sum of q and r, then which one of the following must equal q -r ?
Ap−rBp+rCp−2rDp+2r
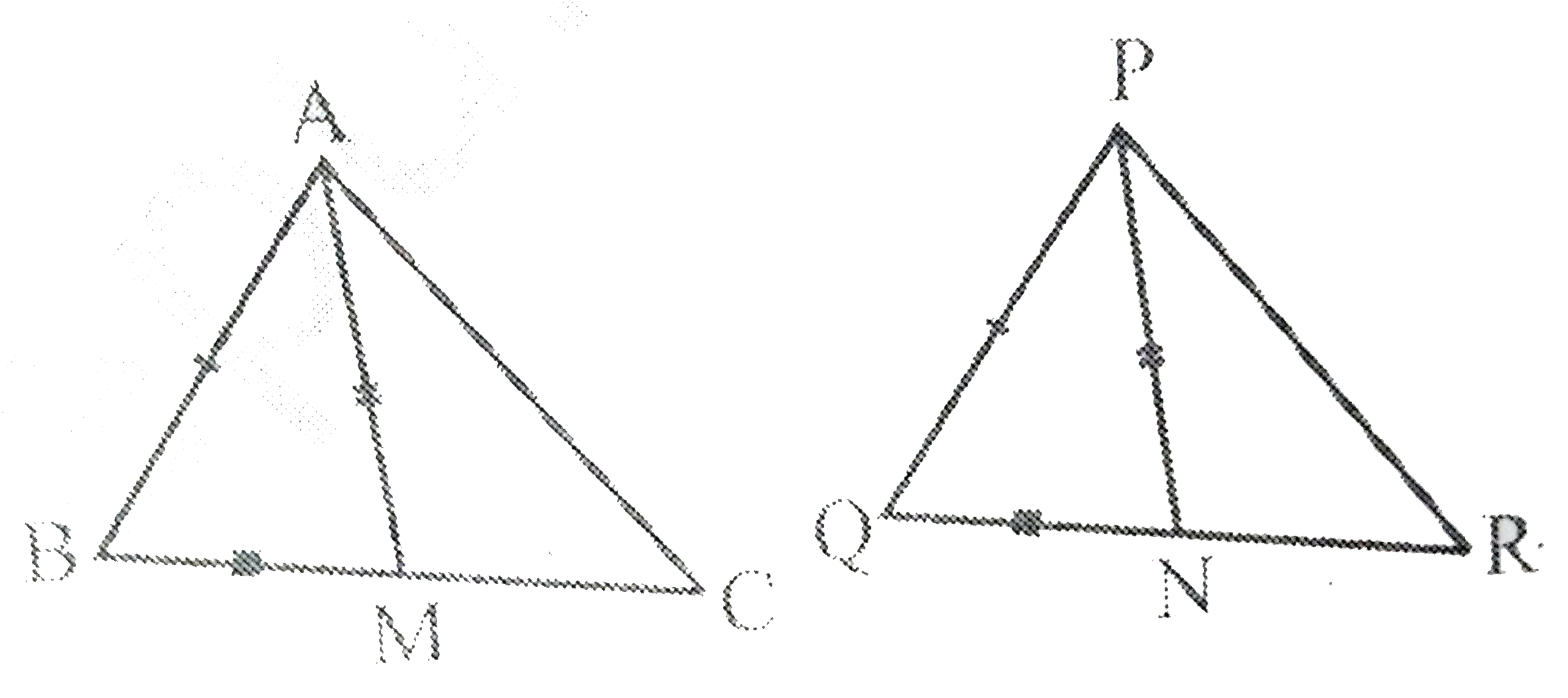
Two sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionLet Δ denote the area of the ΔABCandΔp be the area of its pedal triangle. If Δ=kΔp, then k is equal to
View SolutionIn a ΔPQR, if ∠P=90∘ and ∠Q=∠R, find the measures of each of the equal angles of the triangle.
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are a. (43,3) b. (3,23) c. (3,43) d. (43,23)
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are (43,3) (b) (3,23) (3,43) (d) (43,23)
View Solution
