Let f(x)=⎧⎪
⎪⎨⎪
⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima
Video Solution
Text Solution
We have f(x)=⎧⎪
⎪⎨⎪
⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π
y=x2+3x
∴ y=(x+3/2)2−9/4
∴ (y+9/4)=(x+3/2)2 which is a parabola having vertex at (−3/2,−9/4).
For y=−sinx,y=0 when x = 0 and y = -1 when x=π/2.
For y = -1 - cos x, y = -1 when x=π/2 and y = 0 when x=π.
Hence the graph of the function y = f(x) is as shown in the following figure.
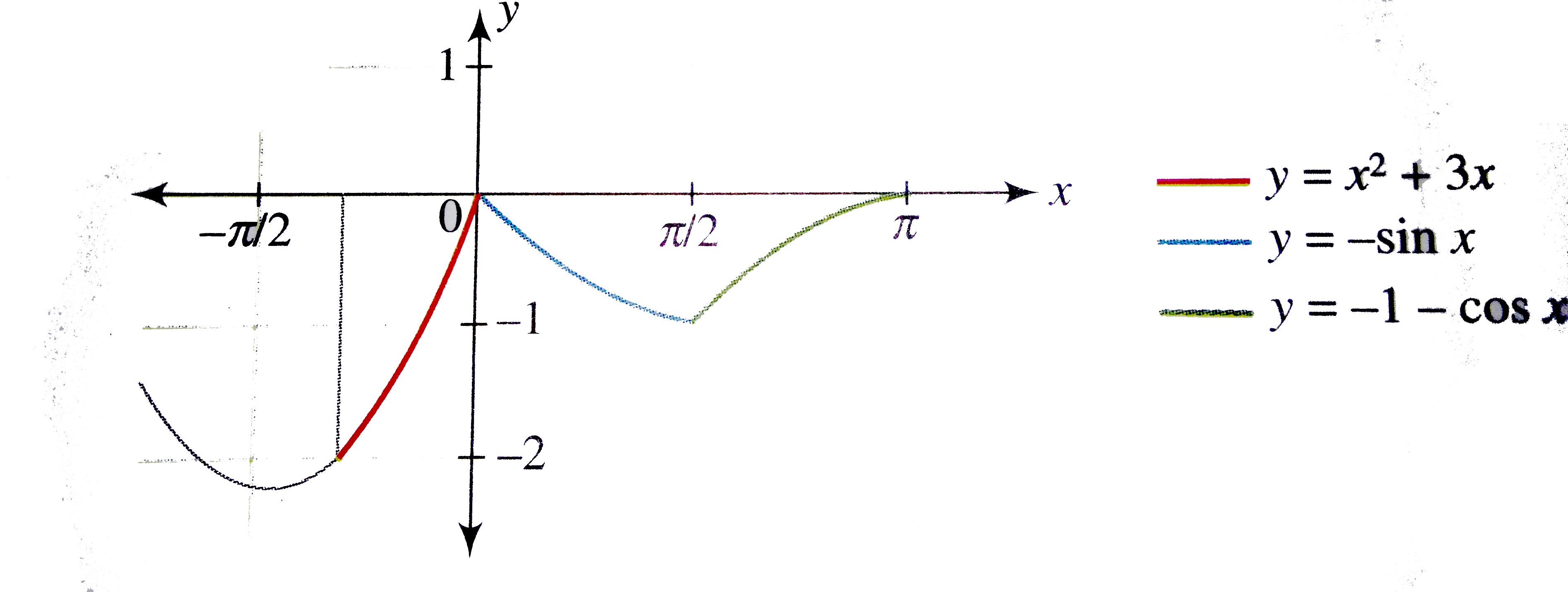
From the graph, x=π/2 is the point of local minima.
for y=−sinx,y''=sinx>0 for x∈(0,π/2). SO the curve is concave upwards.
For y=−1−cosx,y''=cosx<0 for x∈(π/2,π). So the curve is concave downwards.
Hence x=π/2 is the point of inflection.
The least value of y=f(x) occurs for y=x2+3x, when x = -1.
Hence the least value is -2. Therefore, the range is [-2, 0].
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Knowledge Check
Let f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤π then f(x) has
Alocal maximum at x=π2Blocal minimum at x=π2Cabsolute minimum at x=0,πDabsolute maximum at x=π2Let f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤x then f(x) has
Alocal maximum at x=π/2Blocal minima at x=π/2Cabsolute minima at x = 0,πDabsolute maxima at x=π/2Let f(x)=⎧⎪⎨⎪⎩x2+4x,−3≤x≤0−sinx,0<x≤π/2−cosx−1,π/2<x≤π
which one of the following is not true ?Ax=-2 is the point of global minimumBx=π is the point of global maximumCf(x) is not differentiable at x=π2Df(x) is discontinunous at x=0
Let f(x)=⎧⎪⎨⎪⎩sgn(x)+x,−∞<x<0−1+sinx,0≤x≤π/2cosx,π/2≤x<∞, then number of points, where f(x) is not differentiable, is/are
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤x Then at x=π2, f(x) has:
View SolutionLetf(x)={x+20≤x<26−xx≥2,g(x)={1+tanx0≤x<π43−cotxπ4≤x<π
the range of f(x)=g(x)) is
View SolutionIf f(x)={xsinx, for 0<x≤π2π2sin(π+x), for π2<x<π, then
View SolutionLet f(x)={xfor0≤x<13−xfor1≤x≤2
Then f(x) is
View Solution
