Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Video Solution
Text Solution
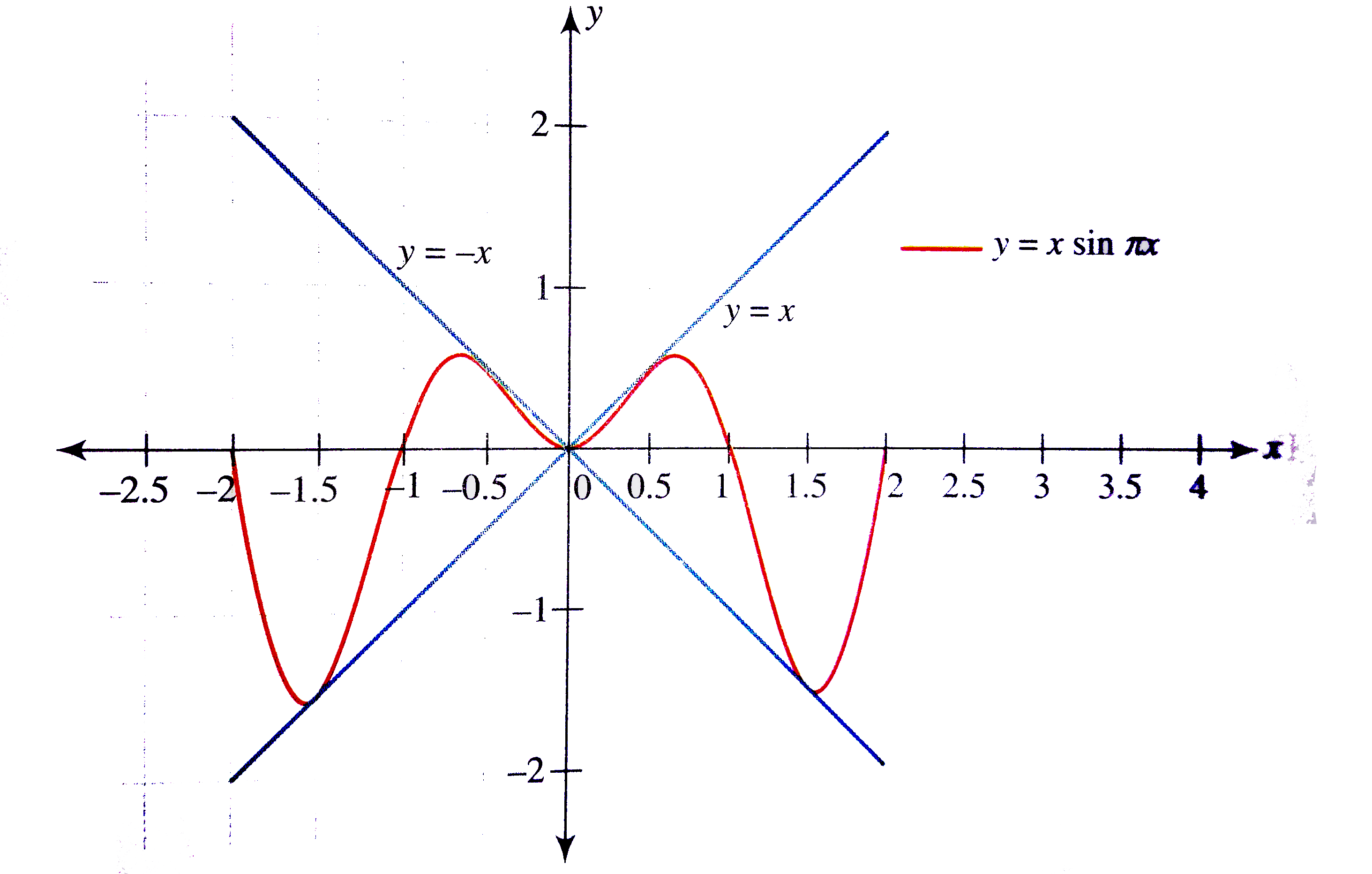
From the graph, 0≤xsinπx<1, for x∈[−1,1]
Hence f(x)=0,∀x∈[−1,1]
Thus, correct answers are (a), (b) and (d).
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Knowledge Check
Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x = 0Bcontinuous in (−1,0)Cdifferentiable at x = 1Ddifferentiable in (−1,1)Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x=0,Bcontinuous in (-1,0),Cdifferentiable at x = 1Ddifferentiable in (-1,1),If the function f:R→R be such that f(x)=x−[x], where [x] denotes the greatest integer less than or equal to k, then f−1(x) is :
Aa. [x]−xBb. 1x−[x]Cc. not definedDd. none of these
If the function f:R→R be such that f(x)=x−[x], where [x] denotes the greatest integer less than or equal to x, then f−1(x) is
View SolutionLet [x] denote the greatest integer less than or equal to x. If x=(√3+1)5, then [x] is equal to
View SolutionIf f(x)=⎧⎨⎩sin[x][x], for [x]≠00, for [x]=0where [x] denotes the greatest integer less than or equal to x. Then find limx→0f(x).
View SolutionIf f(x)=sin−1([x]+x)[x],[x]≠0
=0, [x] = 0 where [x] denotes the greatest integer less than or equal to x, then limx→0f(x) is
View SolutionLet [x] denote the greatest integer less than or equal to x. Then, ∫−11[x]dx=?
View Solution
