On a common hypotenuse AB, two right angled triangles, ACB and ADB are situated on opposite sides. Prove that ∠BAC=∠BDC.
To prove that ∠BAC=∠BDC for the triangles ACB and ADB situated on opposite sides of the common hypotenuse AB, we will follow these steps:
1. Draw the Diagram:
- Start by drawing the line segment AB, which will be the common hypotenuse.
- Construct two right-angled triangles ACB and ADB such that they are on opposite sides of AB.
- Label the points: A, B, C, and D where A and B are the endpoints of the hypotenuse, and C and D are the vertices of the right-angled triangles.
2. Identify Angles:
- In triangle ACB, identify the right angle at C (i.e., ∠ACB=90∘).
- In triangle ADB, identify the right angle at D (i.e., ∠ADB=90∘).
- We need to prove that ∠BAC=∠BDC.
3. Use the Property of Cyclic Quadrilaterals:
- Since triangles ACB and ADB are situated on opposite sides of the hypotenuse AB, we can consider the quadrilateral ACBD.
- The sum of the angles in a quadrilateral is 360∘. Therefore, ∠ACB+∠ADB+∠BAC+∠BDC=360∘.
- Since ∠ACB=90∘ and ∠ADB=90∘, we have:
90∘+90∘+∠BAC+∠BDC=360∘
- Simplifying this gives:
∠BAC+∠BDC=180∘
4. Conclude that ACBD is a Cyclic Quadrilateral:
- Since ∠ACB+∠ADB=180∘, quadrilateral ACBD is a cyclic quadrilateral (the opposite angles of a cyclic quadrilateral are supplementary).
5. Use the Inscribed Angle Theorem:
- In a cyclic quadrilateral, angles subtended by the same arc are equal. Here, angles ∠BAC and ∠BDC are subtended by the same arc BC.
- Therefore, we can conclude that:
∠BAC=∠BDC
Final Conclusion:
Thus, we have proved that ∠BAC=∠BDC.
- Start by drawing the line segment AB, which will be the common hypotenuse.
- Construct two right-angled triangles ACB and ADB such that they are on opposite sides of AB.
- Label the points: A, B, C, and D where A and B are the endpoints of the hypotenuse, and C and D are the vertices of the right-angled triangles.
- In triangle ACB, identify the right angle at C (i.e., ∠ACB=90∘).
- In triangle ADB, identify the right angle at D (i.e., ∠ADB=90∘).
- We need to prove that ∠BAC=∠BDC.
- Since triangles ACB and ADB are situated on opposite sides of the hypotenuse AB, we can consider the quadrilateral ACBD.
- The sum of the angles in a quadrilateral is 360∘. Therefore, ∠ACB+∠ADB+∠BAC+∠BDC=360∘.
- Since ∠ACB=90∘ and ∠ADB=90∘, we have:
90∘+90∘+∠BAC+∠BDC=360∘
- Simplifying this gives:
∠BAC+∠BDC=180∘
- Since ∠ACB+∠ADB=180∘, quadrilateral ACBD is a cyclic quadrilateral (the opposite angles of a cyclic quadrilateral are supplementary).
- In a cyclic quadrilateral, angles subtended by the same arc are equal. Here, angles ∠BAC and ∠BDC are subtended by the same arc BC.
- Therefore, we can conclude that:
∠BAC=∠BDC
Thus, we have proved that ∠BAC=∠BDC.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.2
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Show that in a right angled triangle, the hypotenuse is the longest side.
View SolutionProve that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
View SolutionProve that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
View SolutionProve that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
View SolutionIn an isosceles triangle, prove that the angles opposite to equal sides are equal.
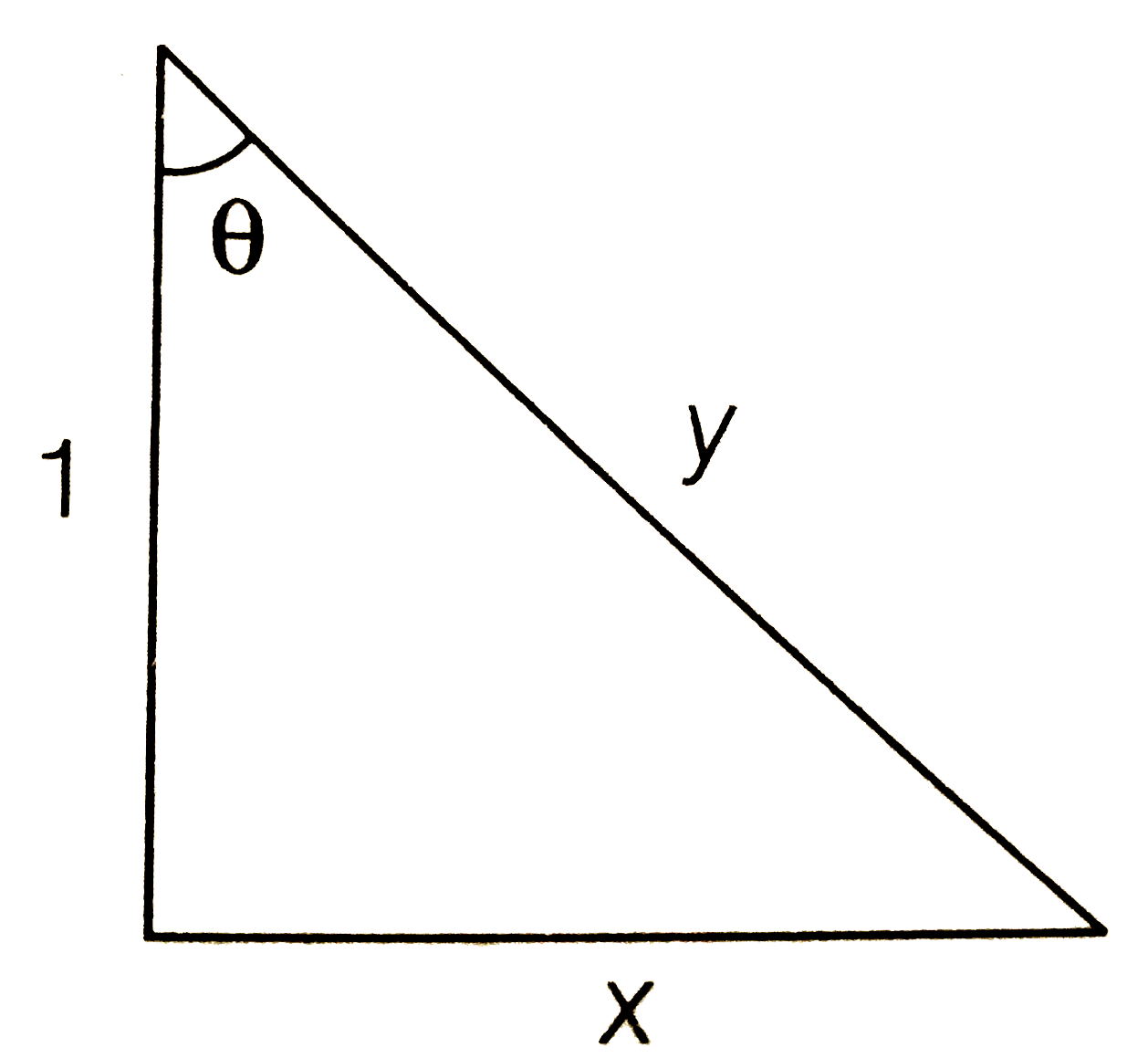
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionA circle touches the hypotenuse of a right angled triangle at its middle point and passes through the mid-point of the shorter side. If aandb(a<b) be the lengths of the sides, then prove that the radius of the circle is b4a√a2+b2
View SolutionA point on the hypotenuse of a right triangle is at distances a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is (a23+b23)32
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View Solution
