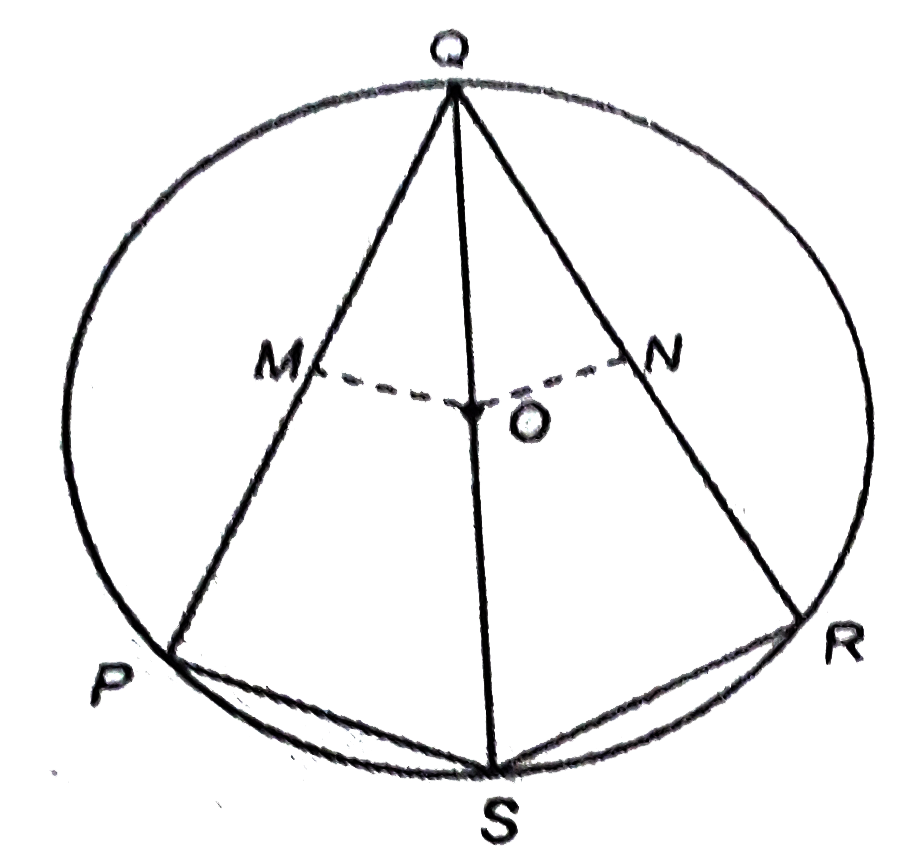
PQ and RQ are chords of a circle equidistant from the centre. Prove that the diameter passing through Q visects ∠PQR and ∠PSR
Draw OM and ON perpendicular from O to PQ and QR respectively.
In ΔQOM and ΔQON,
∵ ⎧⎪⎨⎪⎩OM=ON(given)∠QMO=∠QNO(each90∘)QO=QO(common)
∴ΔQOM≅ΔQON (R.H.S.)
⇒∠MQO=∠NQO
Now, QS is the diameter of the circle. ∴∠QPS=∠QRS=90∘ (∵∠ in a semicircle is right angle)
In ΔQPS and ΔQRS,
∵ ⎧⎪⎨⎪⎩∠QPS=∠QRS=90∘QS=QS(common)∠PQS=∠RQS(proved above)
∴ΔQPS≅ΔQRS
⇒∠PSQ=∠RSQ
∴QS, bisects ∠PQR and ∠PSR.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
PQ and RQ are chords of a circle equidistant from the centre. Prove that the diameter passing through Q bisects ∠PQR and ∠PSR
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ.
View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on the same side of centre O
View SolutionPQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR=120o , then ∠OPQ is 60o (b) 45o (c) 30o (d) 90o
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
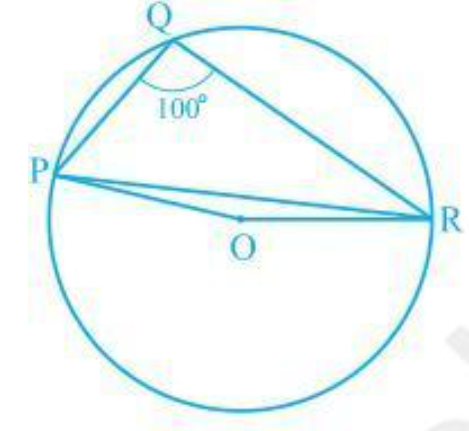
View SolutionIn Figure, ∠PQR=1000, where P, Q and R are points on a circle with centre. O. Find ∠OPR
View SolutionIn Figure, TQ and TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=800and ∠PRT=300, determine ∠TQR and ∠QTR
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionFind the coordinates of points P, Q, R and S in Figure.
View Solution
