PQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
To prove that PM2=QM⋅MR in triangle PQR where P is the right angle and PM is perpendicular to QR, we can follow these steps:
Step 1: Understand the Configuration
We have triangle PQR with P as the right angle. Point M lies on side QR such that PM is perpendicular to QR.
Step 2: Apply the Pythagorean Theorem
In triangle PQR, since P is the right angle, we can apply the Pythagorean theorem:
QR2=PQ2+PR2(1)
Step 3: Apply the Pythagorean Theorem in Triangles PMQ and PMR
In triangle PMQ:
PQ2=PM2+QM2(2)
In triangle PMR:
PR2=PM2+MR2(3)
Step 4: Substitute PQ2 and PR2 into Equation (1)
From equations (2) and (3), we can express PQ2 and PR2 in terms of PM, QM, and MR:
QR2=(PM2+QM2)+(PM2+MR2)
Step 5: Simplify the Equation
Combining the two expressions gives:
QR2=2PM2+QM2+MR2
Step 6: Rearranging the Equation
We can rearrange this equation to isolate PM2:
2PM2=QR2−QM2−MR2
Step 7: Use the Relationship of Segments
Since QM+MR=QR, we can express QR2 as:
QR2=(QM+MR)2=QM2+2QM⋅MR+MR2
Step 8: Substitute Back
Substituting this back into our equation gives:
2PM2=(QM2+2QM⋅MR+MR2)−QM2−MR2
This simplifies to:
2PM2=2QM⋅MR
Step 9: Divide by 2
Dividing both sides by 2 results in:
PM2=QM⋅MR
Conclusion
Thus, we have shown that:
PM2=QM⋅MR
We have triangle PQR with P as the right angle. Point M lies on side QR such that PM is perpendicular to QR.
In triangle PQR, since P is the right angle, we can apply the Pythagorean theorem:
QR2=PQ2+PR2(1)
In triangle PMQ:
PQ2=PM2+QM2(2)
PR2=PM2+MR2(3)
From equations (2) and (3), we can express PQ2 and PR2 in terms of PM, QM, and MR:
QR2=(PM2+QM2)+(PM2+MR2)
Combining the two expressions gives:
QR2=2PM2+QM2+MR2
We can rearrange this equation to isolate PM2:
2PM2=QR2−QM2−MR2
Since QM+MR=QR, we can express QR2 as:
QR2=(QM+MR)2=QM2+2QM⋅MR+MR2
Substituting this back into our equation gives:
2PM2=(QM2+2QM⋅MR+MR2)−QM2−MR2
This simplifies to:
2PM2=2QM⋅MR
Dividing both sides by 2 results in:
PM2=QM⋅MR
Thus, we have shown that:
PM2=QM⋅MR
Topper's Solved these Questions
Similar Questions
PQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionIn △PQR, right angled at Q, tanP−cotR is:
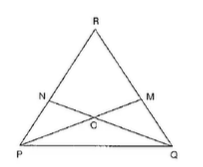
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
 View Solution
View Solution1. Let PQR be a right angled isosceles triangle, right angled at P (2,1). If the equation of the line QR is 2x + y 3, then the equation representing the pair of (1999, 2M) lines P and PR is
View SolutionIn a triangle PQR, right angled at Q. PQ=5 cm, QR=12 cm. Find the length of QM , if M is the mid point of PR .
View SolutionIn ΔABC and ΔPQR,∠B=∠Q,∠C=∠R. M is the mid-point of side QR. If AB : PQ = 7 : 4, then
area (ΔABC)area (ΔPMR) is :
 View Solution
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
 View Solution
View SolutionABC is a triangle and PQ is a straight line meeting AB in P and AC in Q . If AP=1cm , PB=3cm , AQ=1.5cm , QC=4.5m , prove that area of APQ is one-sixteenth of the area of ABC .
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View Solution

