PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
To prove that lines LM and QS bisect each other in parallelogram PQRS, where PL = MR, we can follow these steps:
Step 1: Draw the Parallelogram
Draw parallelogram PQRS with points P, Q, R, and S. Mark points L on PQ and M on SR such that PL = MR.
Hint: Remember that in a parallelogram, opposite sides are equal and parallel.
Step 2: Establish Relationships
Since PL = MR, we can express the segments in terms of the lengths of the sides of the parallelogram:
- Let PL = x, then LQ = PQ - PL = PQ - x.
- Let MR = x, then MS = SR - MR = SR - x.
Hint: Use the property of parallelograms that opposite sides are equal (PQ = SR).
Step 3: Use the Properties of Parallelograms
Since PQ || SR, we can use the properties of alternate interior angles:
- Angle PQL = Angle RSM (alternate interior angles).
- Angle QLP = Angle SML (alternate interior angles).
Hint: Recall that when two lines are cut by a transversal, the alternate interior angles are equal if the lines are parallel.
Step 4: Consider Triangles SMT and LTQ
Now, consider triangles SMT and LTQ:
- We have Angle PQL = Angle RSM (from step 3).
- We have Angle QLP = Angle SML (from step 3).
- Also, we have SM = LQ (since we established earlier that SM = SR - MR = PQ - PL = LQ).
Hint: Use the Angle-Side-Angle (ASA) congruence criterion for triangles.
Step 5: Prove Triangle Congruence
By the ASA criterion, triangles SMT and LTQ are congruent:
- Therefore, we can conclude that ST = TQ and LT = TM.
Hint: When two triangles are congruent, corresponding parts are equal.
Step 6: Conclusion
Since ST = TQ and LT = TM, point T bisects both segments LM and QS. Thus, LM and QS bisect each other.
Hint: Summarize your findings by stating that you have shown the required property using congruence and properties of angles.
Final Statement
Therefore, we have proved that lines LM and QS bisect each other in parallelogram PQRS, given that PL = MR.
---
Draw parallelogram PQRS with points P, Q, R, and S. Mark points L on PQ and M on SR such that PL = MR.
Since PL = MR, we can express the segments in terms of the lengths of the sides of the parallelogram:
- Let PL = x, then LQ = PQ - PL = PQ - x.
- Let MR = x, then MS = SR - MR = SR - x.
Since PQ || SR, we can use the properties of alternate interior angles:
- Angle PQL = Angle RSM (alternate interior angles).
- Angle QLP = Angle SML (alternate interior angles).
Now, consider triangles SMT and LTQ:
- We have Angle PQL = Angle RSM (from step 3).
- We have Angle QLP = Angle SML (from step 3).
- Also, we have SM = LQ (since we established earlier that SM = SR - MR = PQ - PL = LQ).
By the ASA criterion, triangles SMT and LTQ are congruent:
- Therefore, we can conclude that ST = TQ and LT = TM.
Since ST = TQ and LT = TM, point T bisects both segments LM and QS. Thus, LM and QS bisect each other.
Therefore, we have proved that lines LM and QS bisect each other in parallelogram PQRS, given that PL = MR.
Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 3 MARKS QUESTIONS
11 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
ABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
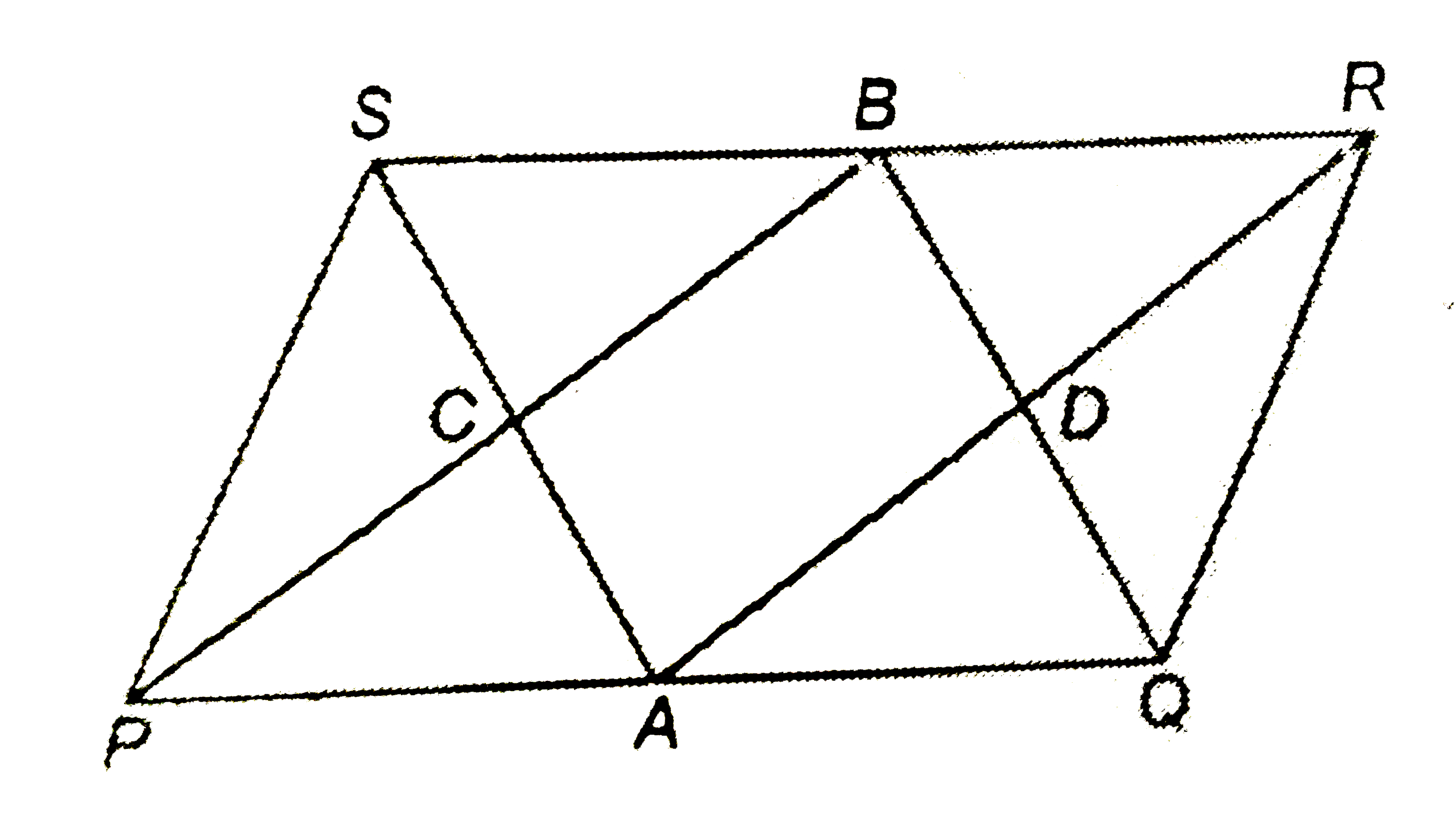
View SolutionIn the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionIn ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionPQRS is a parallelogram. RA and RB are perpendiculars from R on PQ and PS, respectively. If RA = 15 cm, RB = 22 cm, and QR = 26 cm, find PQ.
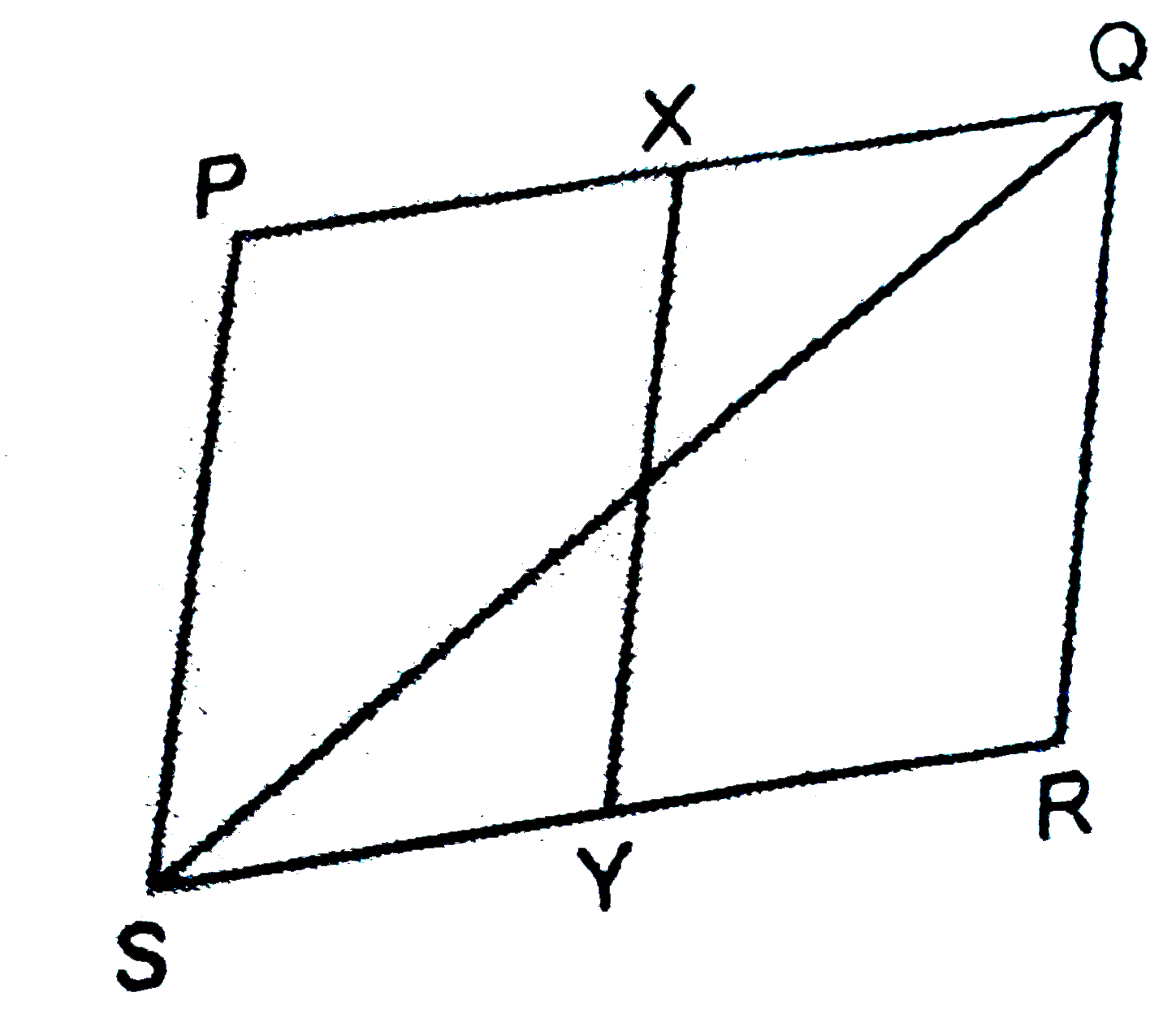
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram. Figure
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionPoints P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
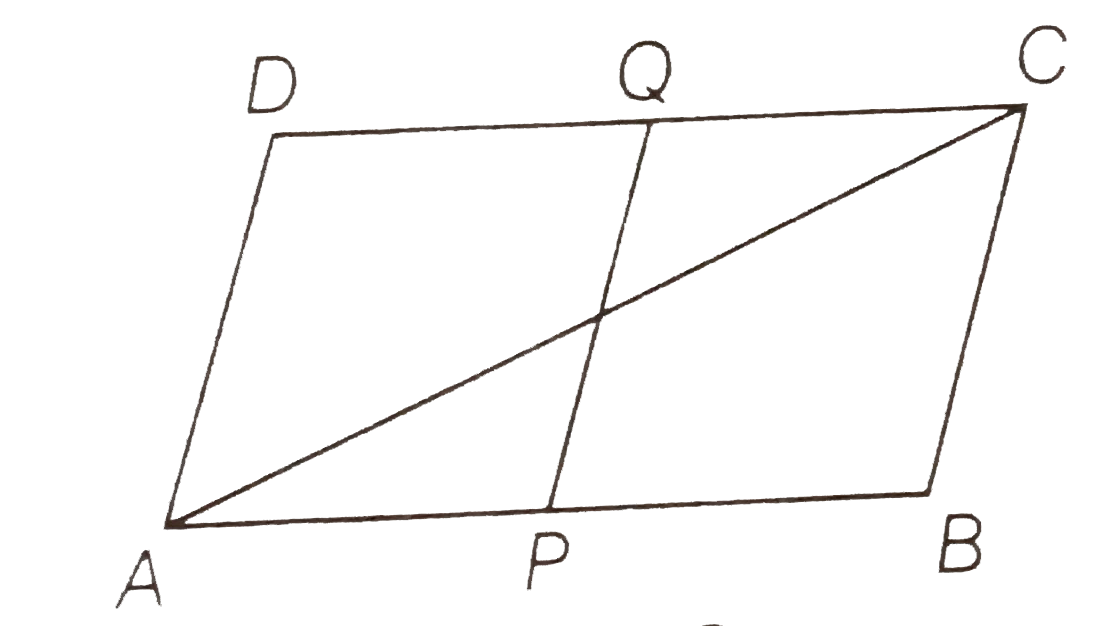
View Solution
