Prove that sinx+2x≥3x(x+1)π,∀x∈[0,π2] (Justify the inequality, if any used).
Video Solution
Text Solution
Let f(x)=sinx+2x−3x(x+1)π
∴ f'(x)=cosx+2−3π(2x+1)
Let f'(x)=0
∴ cosx=6πx+3π−2
Now draw the graphs of y = cos x and y=6πx+3π−2 as shown in the following figure.
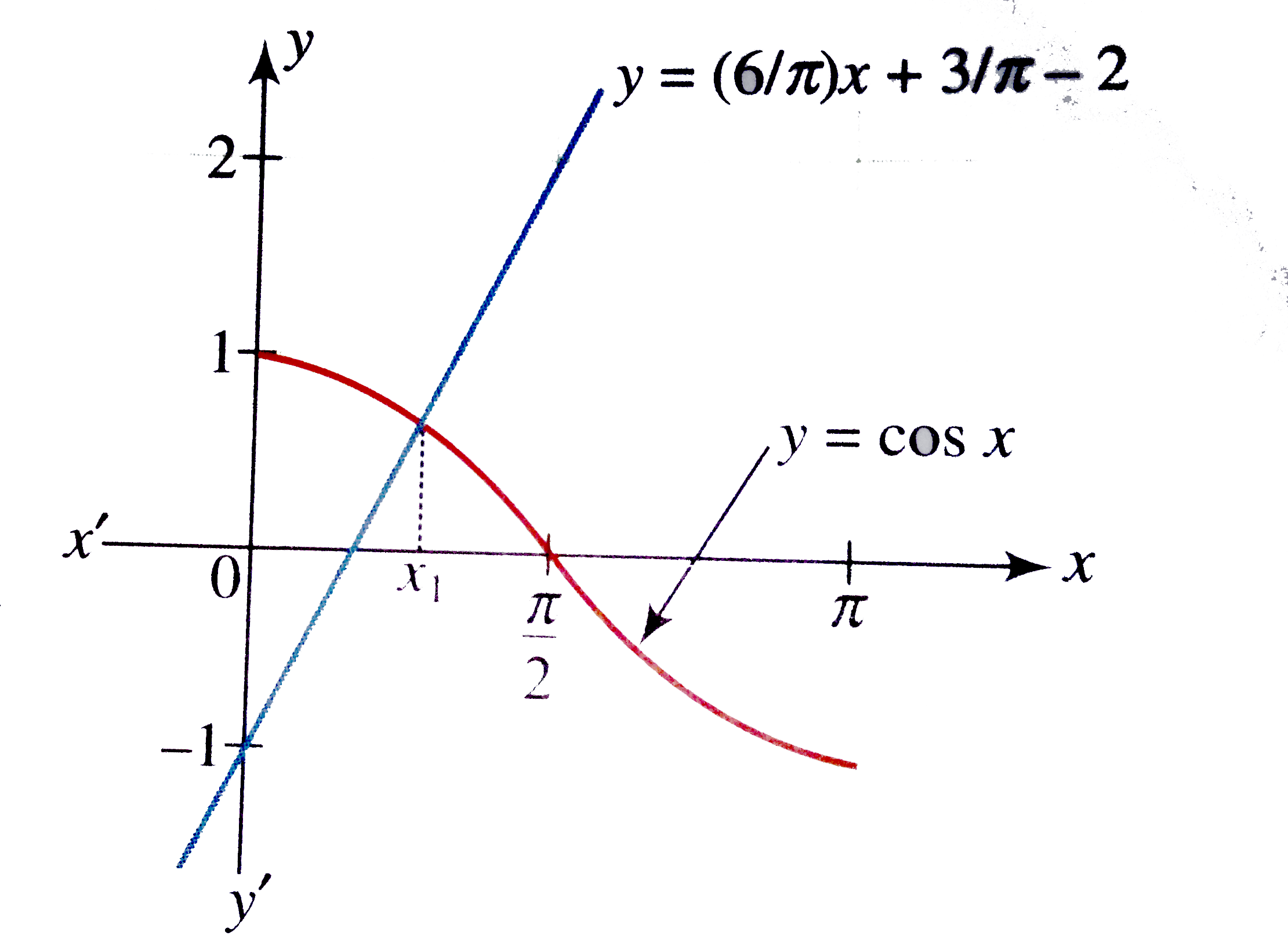
The graphs of y = cos x and y=6πx+3π−2 intersect only once.
From the graph, f'(x)=0 for some x=x1∈[0,π2]
For x<x1, the graph of y = cos x lies above the graph of y=6πx+3π−2
For x>x1, the graph of y = cos x lies below the graph of y=6πx+3π−2
Thus, f'(x)>0 for x<x1, where f(x) increases, and f'(x)<0 for x>x1, Where f(x) decreases.
Also f''(x)=−sinx−3π(2)<0, so the graph is concave downwards.
So x=x1 is the point of maxima.
f(0)=0,f(π2)=π4−12
Graph of y = f(x) is as shown in the following figure.
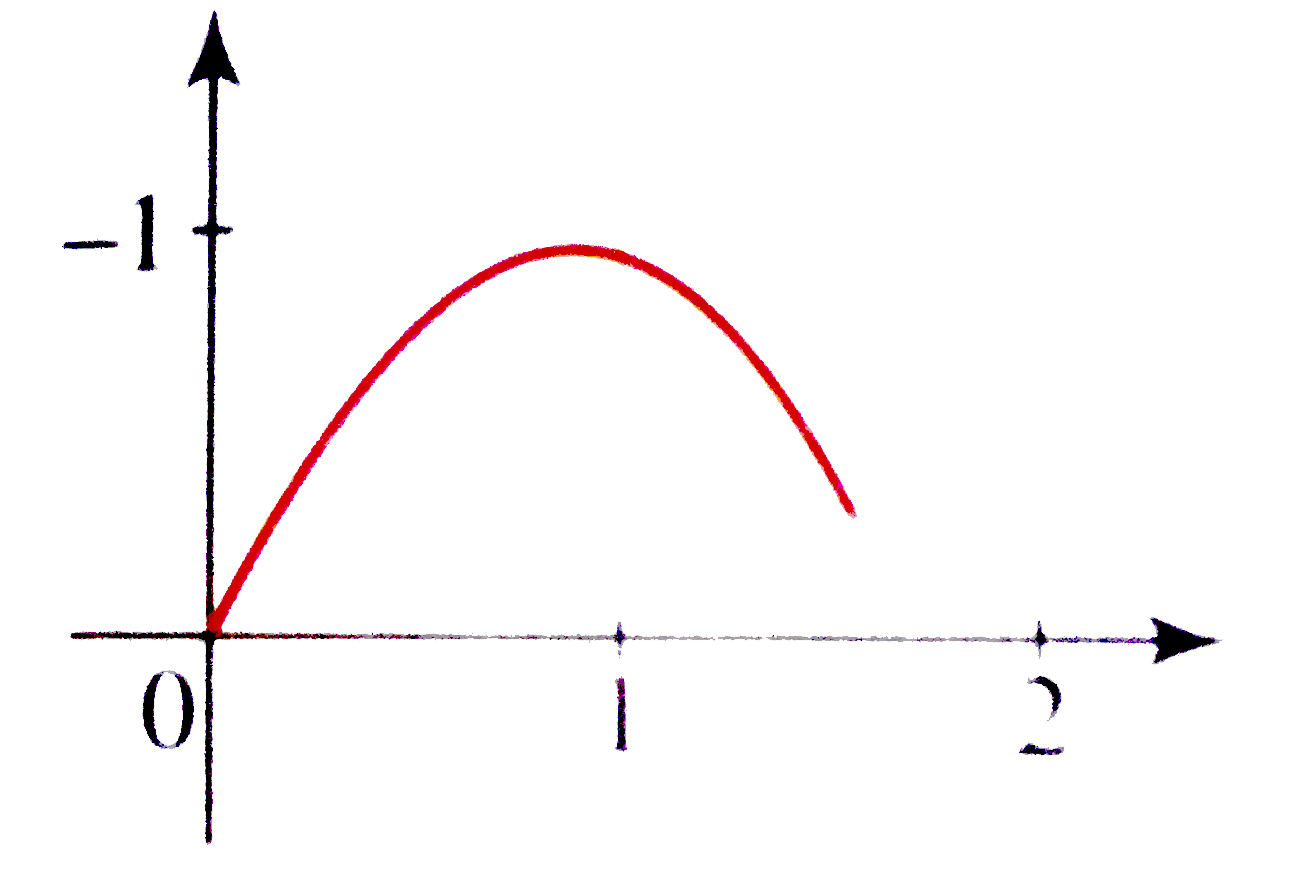
The graph lies completely above the x - axis, so f(x)>0.
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
Similar Questions
Knowledge Check
If sinx+x≥|k|x2,∀x∈[0,π2], then the greatest value of k is
A−2(2+π)π2B2(2+π)π2Ccan't be determined finitelyDzeroIf f(x)=2sinx−x2, then in x∈[0,π]
Af(x) has no local maximumBf(x) has one local minimumCf(x) has 2 local maximaDf(x) has one local maximum
prove that cos−1(sinx)=π2−x
View SolutionUsing the relation 2(1−cosx)<x2,x≠0 or otherwise, prove that s∈(tanx)≥x,∀x∈[0,π4].
View SolutionFind the values of x in the interval [0,2π] which satisfy the inequality:
3|2sinx−1|≥3+4cos2x
View SolutionProve that following inequalities sinx≤x≤tanx ∀ ∈[0,π2]
View SolutionFind the values of x in the interval [0, 2π] which satisfy the inequality : 3 |sinx−1|≥3+4cos2x.
View SolutionShow that 0<xsinx−12sin2x<(π−1)2,∀x∈(0,π2).
View Solution
