Solve : 2cos2θ+sinθ≤2, where π/2≤θ≤3π/2.
Video Solution
Text Solution
2cos2θ+sinθ≤2
⇒ 2(1−sin2θ)+sinθ≤2
⇒ −2sin2θ+sinθ≤0
⇒ 2sin2θ−sinθ≥0
⇒ sinθ(2sinθ−1)≥0
⇒ sinθ(sinθ−1/2)≥0,
which is possible if sinθ≤0 or sinθ≥1/2
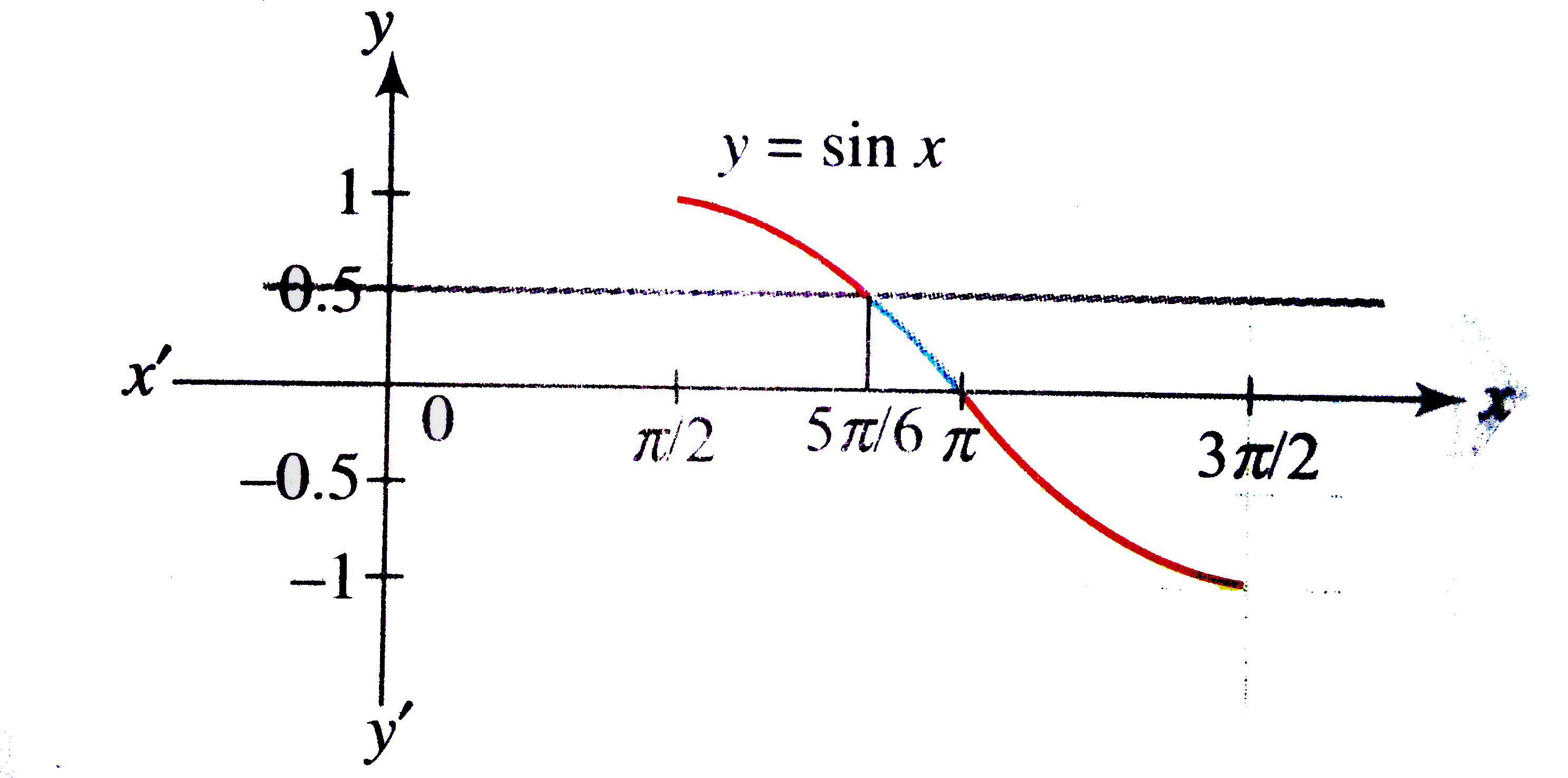
Now sinθ≥1/2⇒π/2≤θ≤5π/6 (from the figure)
And sinθ≤0⇒π≤θ≤3π/2 (from the figure)
Hence the required values of θ are given by θ∈[π/2,5π/6]∪[π,3π/2]
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
Similar Questions
Knowledge Check
ifA=(θ:2cos2θ+sinθ≤2) and
b={θ:π2≤θ≤3π2}, then A∩B is equal toA{θ:π/2≤θ≤5π/6}B{θ:π≤θ≤3π/2}C{θ:π/2≤θ≤5π6}∪{θ:π≤θ3π/2}Dnone of theseIf A={θ:2cos2θ+sinθ≤2}and
B={θ:π2≤θ≤3π2}. Then , A∩B is equal toA{θ:π/2≤θ≤5π/6}B{θ:π≤θ≤3π/2}C{θ:π/2≤θ≤5π/6}∪{θ:π≤θ≤3π/2}DNone of the aboveIf 2sin2θ=3cosθ,0≤θ≤2π,θ =
Aπ/6,5π/6Bπ/3,2π/3Cπ/3,5π/3Dπ/2,π