The circumcentre of the ΔABC is O. Prove that ∠OBC+∠BAC=90∘.
Video Solution
Text Solution
Given A circle is circumscribed on a ΔABC having centre O.
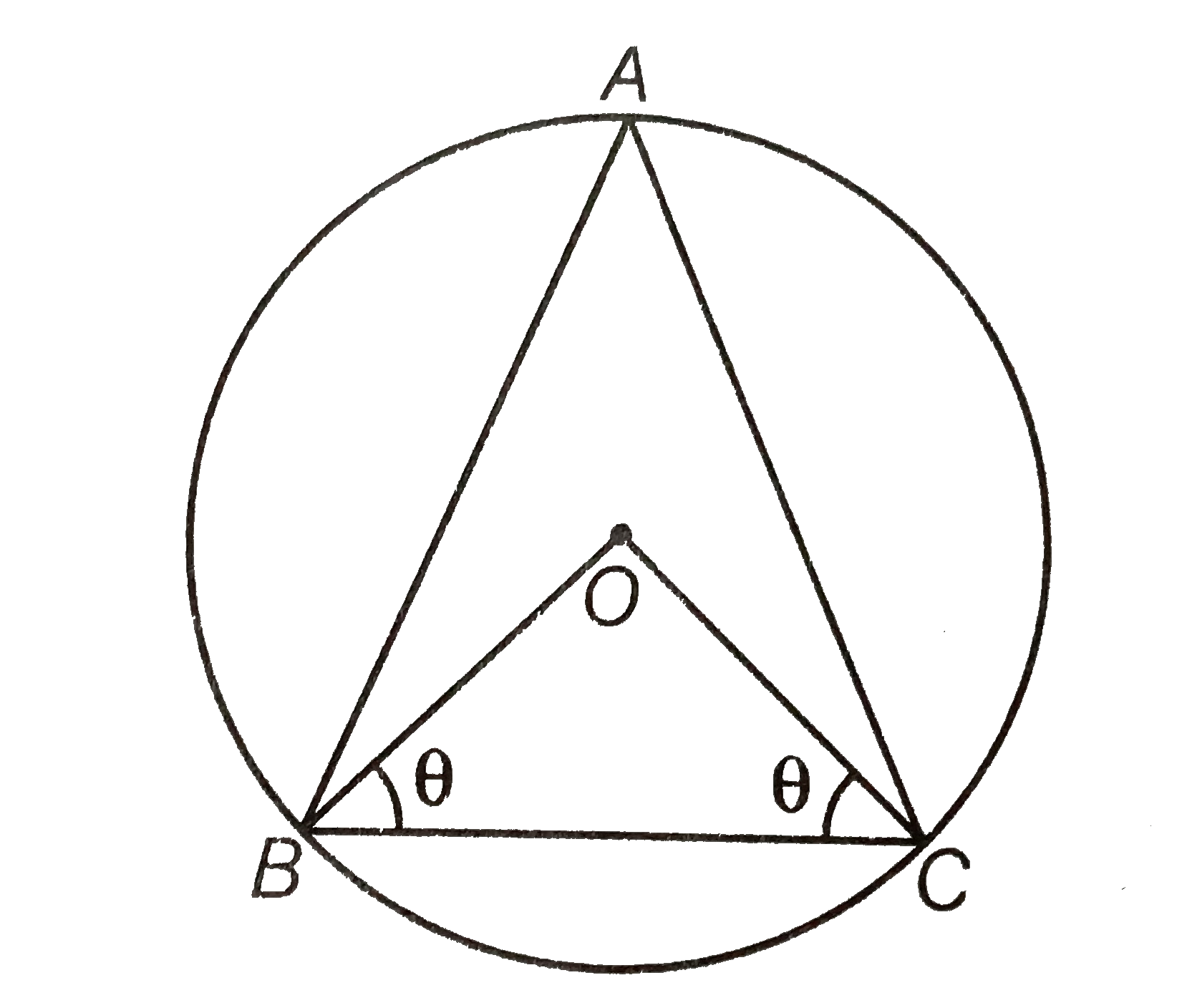
To prove ∠OBC+∠BAC=90∘
Construction Join BO and CO.
Proof Let ∠OBC=∠OCB=θ…(i)
In ΔOBC,∠BOC+∠OCB+∠CBO=180∘
[by angle sum property of a triangle is 180∘]
⇒∠BOC+θ+θ=180∘
⇒∠BOC=180∘−2θ
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴∠BOC=2∠BAC
⇒∠BAC=∠BOC2=180∘−2θ2=90∘−θ
⇒∠BAC+θ=90∘
∴∠BAC+∠OBC=90∘ [from Eq. (i)]
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
A40∘B50∘C60∘D80∘O is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
A3.015 cm.B3.205 cm.C3.025 cm.D3.125 cm.O is the circumcentre of a triangle ABC. If ∠BAC=85∘and∠BCA=75∘ then what is the value of ∠OAC?
A40∘B60∘C70∘D90∘
O is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
View SolutionIn ΔABC,AD⊥BCandAD2=BD⋅CD . Prove that ∠BAC=90∘ .
View SolutionO is orthocentre of ΔABC if ∠BOC=120∘ find ∠BAC
View SolutionIf O is a circumcentre of ΔABC and OD⊥BC the find ∠BOD?
View SolutionIf O is the circumcentre of ΔABC and OD ⊥ BC, then ∠BOD must be equal to
View Solution
