The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long ,Calculate : its volume
The correct Answer is:5460m3
To calculate the volume of the tunnel, we need to consider the cross-section, which consists of a square and a semicircle. Here’s a step-by-step solution:
Step 1: Understand the dimensions of the cross-section
The cross-section of the tunnel is a square with a side length of 7 m, and it is surmounted by a semicircle.
Step 2: Calculate the area of the square
The area A of a square is given by the formula:
A=side2
For our square:
A=72=49m2
Step 3: Calculate the radius of the semicircle
The semicircle is based on the top side of the square. The diameter of the semicircle is equal to the side of the square, which is 7 m. Thus, the radius r of the semicircle is:
r=72=3.5m
Step 4: Calculate the area of the semicircle
The area A of a semicircle is given by the formula:
A=12πr2
Substituting the radius:
A=12×π×(3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Thus, the area becomes:
A=12×π×12.25=12.25π2=6.125πm2
Using π≈227:
A≈6.125×227=135.757≈19.39m2
Step 5: Calculate the total cross-sectional area
Now, we add the area of the square and the area of the semicircle:
Total Area=Area of Square+Area of Semicircle
Total Area=49+19.39≈68.39m2
Step 6: Calculate the volume of the tunnel
The volume V of the tunnel is given by the formula:
V=Total Area×Length
Given that the length of the tunnel is 80 m:
V=68.39×80
Calculating this gives:
V≈5471.2m3
Final Answer
The volume of the tunnel is approximately 5471.2m3.
---
The cross-section of the tunnel is a square with a side length of 7 m, and it is surmounted by a semicircle.
The area A of a square is given by the formula:
A=side2
For our square:
A=72=49m2
The semicircle is based on the top side of the square. The diameter of the semicircle is equal to the side of the square, which is 7 m. Thus, the radius r of the semicircle is:
r=72=3.5m
The area A of a semicircle is given by the formula:
A=12πr2
Substituting the radius:
A=12×π×(3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Thus, the area becomes:
A=12×π×12.25=12.25π2=6.125πm2
Using π≈227:
A≈6.125×227=135.757≈19.39m2
Now, we add the area of the square and the area of the semicircle:
Total Area=Area of Square+Area of Semicircle
Total Area=49+19.39≈68.39m2
The volume V of the tunnel is given by the formula:
V=Total Area×Length
Given that the length of the tunnel is 80 m:
V=68.39×80
Calculating this gives:
V≈5471.2m3
The volume of the tunnel is approximately 5471.2m3.
Topper's Solved these Questions
Similar Questions
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long Calculate : the surface area of the tunnel (excluding the floor) .
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. Calculate: its floor area. The tunnel is 80 m long.
View Solution
Knowledge Check
A cube has a side of length 1.2×10−2m. Calculate its volume
A1.7×10−6m3B1.73×10−6m3C1.78×10−6m3D1.732×10−6m3
The cross-section of a railway tunnel is a square surmounted by a semi-circle as shown in the figure.
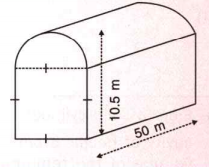
The tunnel is 50 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 10 per m2.
View SolutionThe cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle . The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 2.25 per m2
View SolutionFig. 15.87, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB=90o , calculate: (i) the height of the tunnel (ii) the perimeter of the cross-section (iii) the area of the cross-section.
View SolutionA plot has the shape of a square. Its one side is 24 m long.
Calculate its perimeter.
View SolutionA cube has a side length 1.2×10−2m.Calculate its volume
View SolutionThe cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure, also given that: AM= BN, AB= 7m, CD= 5m. The height of the tunnel is 2.4m. The tunnel is 40m long. Calculate :
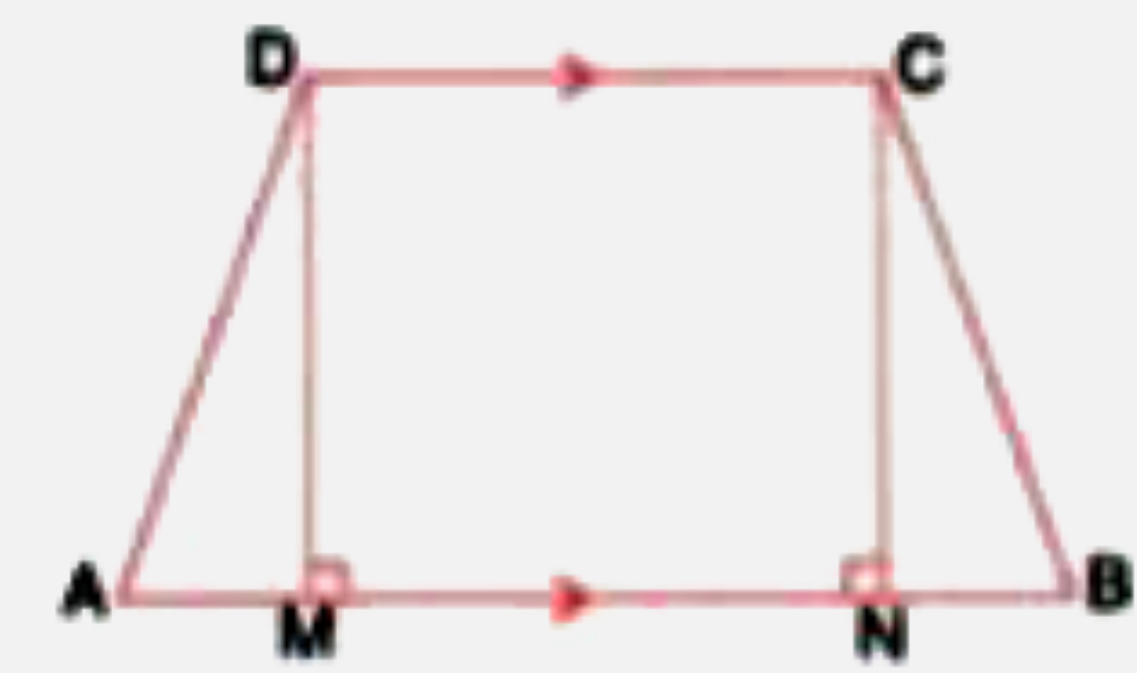
the cost of paying the floor at the rate of Rs 18 per m2.
View SolutionThe cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure, also given that: AM= BN, AB= 7m, CD= 5m. The height of the tunnel is 2.4m. The tunnel is 40m long. Calculate :

the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs 5 per m2 (sq. metre).
View Solution
