The isosceles triangle ABC is inscribed in a circle with centre at O. If AP is a diameter of the circle. Then prove that AP is the bisetors of .Solution in Bengali
Step by step video & image solution for The isosceles triangle ABC is inscribed in a circle with centre at O. If AP is a diameter of the circle. Then prove that AP is the bisetors of angle BPC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Very Short-Answer Type Questions) MCQs
10 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (True or False)
2 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.2 (Short-Answer Type Questions)
7 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
Find the radius of the incircle of the equilateral triangle having each side 12 cm
View SolutionIf the circumcenrtre of the equilateral triangle ABC be P then ∠BPC=120∘
View SolutionO is the circumcentre of ΔABC. If ∠ABC=α∘and∠BCA=β∘, then the find value of ∠BOC.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionIn Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
View SolutionO' is the centre of the inscribed circle in a 30^(@)-60^(@)-90^(@)Delta ABC with right angled at C.If the circle is tangent to AB at D then the angle /_COD is
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionFrom a circle of radius a, an isosceles right angles triangle with the hypotenuse as the diameter of the circle is removed. The distance of the centre of mass of the remaining portion from the centre of the circle is
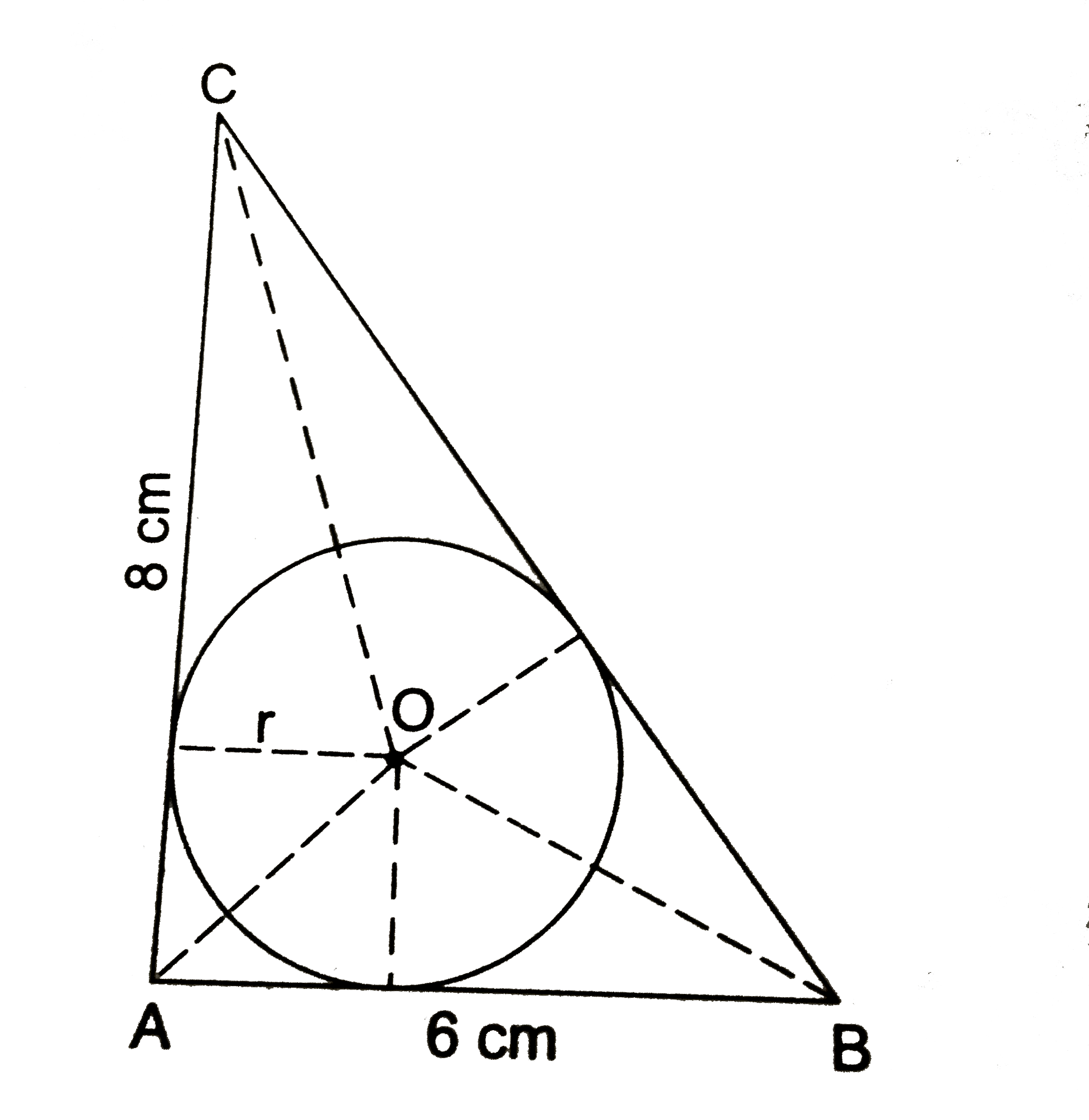
View SolutionIn the given figure ΔABC is right angle at A with AB=6 cm and AC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of r, the radius of the inscribed circle.
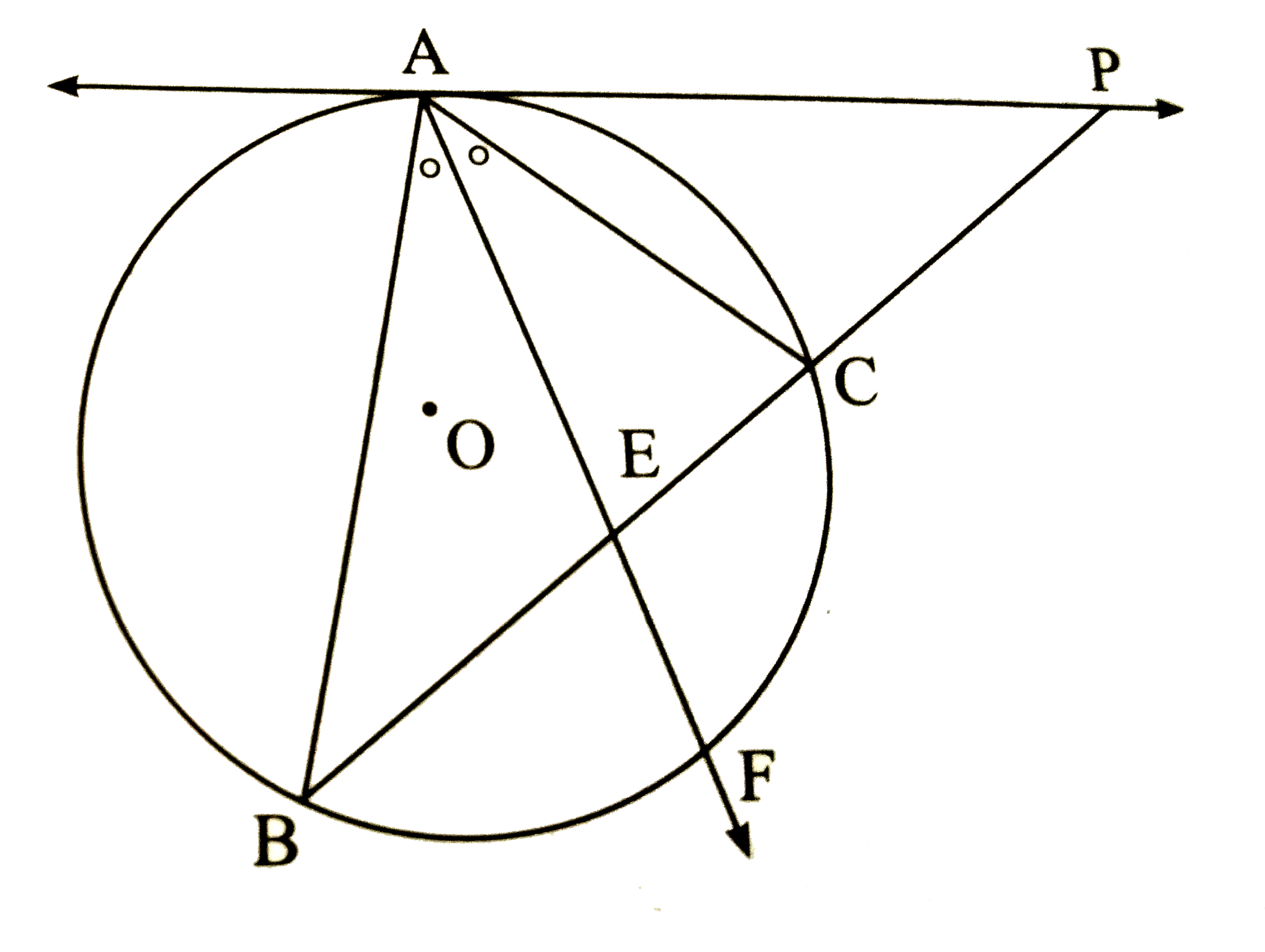
View SolutionΔABC is inscribed in a circle with centre O and line AP is a tangent at the point A. Ray AF is the bisector of ∠BAC
Prove that seg AP≅ seg PE.
View SolutionIn the figure, O is the centre of the circle. Seg AC is the diameter ∠ABC is inscribed in arc ABC and intercepts arc AMC then prove ∠ABC=90∘

View SolutionThe isosceles triangle ABC is inscribed in the circle with centre at O.If AP be a diamtere passing through A, then show that AP is internal bisector of ∠BPC.
View SolutionTriangle ABC is inscribed in a circle, such that AC is a diameter of the circle and angle BAC is 45∘. If the area of triangle ABC is 72 square units, how larger is the area of the circle than the area of triangle ABC ?
View SolutionLet ‘O’ be the centre of a circle, PQ is a diameter, then prove that ∠PRQ=90∘ (OR) Prove that angle in a semi-circle is right angle.
View Solution
