The median BE and CF of a triangle ABC intersect at G. Prove that the area of area of the quadrilateral AFGE.
Video Solution
Text Solution
Given In , medians BE and CF intersect each other at G. To prove
Proof Since, BE is the median of and we know that a median of a triangle divides it into two parts of equal area.
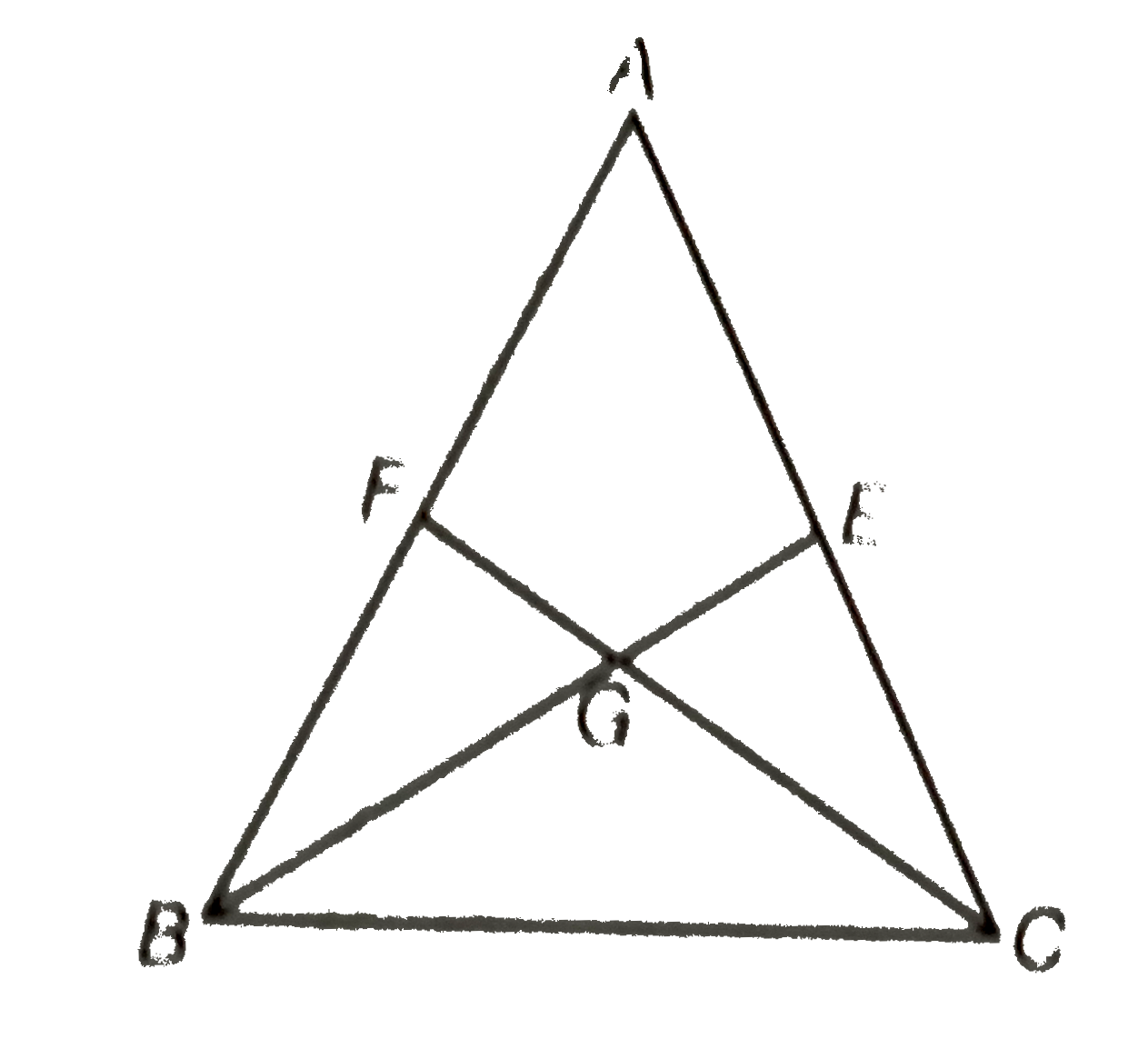
So,
...(i)
Similarly, CF is the median of .
Then,
...(ii)
From Eqs. (i) and (ii),
...(iii)
On substracting from both sides of Eq. (iii), we get
Hence proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
A10 sq.cmB15 sq.cmC20 sq.cmD30 sq.cm - Question 2 - Select One
A triangle PQR is a right angled triangle at Q. E and F are the mid points of QR and PR respectively. What will be the ratio of the area of quadrilateral PQEF to the area of triangle PQR.
एक समकोण त्रिभुज PQR, E पर समकोण है E और F क्रमशः QR और PR के मध्य बिंदु हैं। चतुर्भुज PQEF के क्षेत्रफल और त्रिभुज PQR के क्षेत्रफल का अनुपात क्या होगाA1:1B1:2C2:1D2:3 - Question 3 - Select One
Three medians AD, BE and CF of ΔABC intersect at G. The area of ΔABC is 36 sq. cm. Then the area of ΔCGE is
A12 sq. cmB6 sq. cmC9 sq. cmD18 sq. cm
The medians BE and CF of a triangle ABC intersect at G. Prove that area of GBC=area of quadrilateral AFGE.
View SolutionThe medians BE and CF of a △ABC intersect at G. Then choose the correct option.
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABCView SolutionThe medians of a triangle ABC intersect at
G. Which one of the following is correct ?View SolutionThree medians AD, BE and CF of ΔABC intersect at G. If area of ΔABC is 36 sq cm, then the area of ΔCGE is
View Solution
