The perimeter of a parallelogram ABCD = 40 cm , AB = 3x cm, BC = 2x cm and CD = 2( y+1) cm . Find the values of x and y.
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the properties of a parallelogram
In a parallelogram, opposite sides are equal. Therefore, we can set up equations based on the given information.
Step 2: Set up the equations
Given:
- Perimeter of parallelogram ABCD = 40 cm
- AB = 3x cm
- BC = 2x cm
- CD = 2(y + 1) cm = 2y + 2 cm
Since opposite sides are equal:
- AD = BC = 2x cm
- CD = AB = 3x cm
Step 3: Write the perimeter equation
The perimeter (P) of a parallelogram is given by the formula:
P=2(AB+BC)
Substituting the values we have:
40=2(3x+2x)
Step 4: Simplify the perimeter equation
Now we simplify the equation:
40=2(5x)
40=10x
Step 5: Solve for x
To find x, divide both sides by 10:
x=4010
x=4
Step 6: Use the value of x to find y
Now we know that AB = 3x and CD = 2y + 2. Since AB = CD:
3x=2y+2
Substituting the value of x:
3(4)=2y+2
12=2y+2
Step 7: Solve for y
Now, isolate y:
12−2=2y
10=2y
y=102
y=5
Final Answer
Thus, the values are:
- x=4
- y=5
---
In a parallelogram, opposite sides are equal. Therefore, we can set up equations based on the given information.
Given:
- Perimeter of parallelogram ABCD = 40 cm
- AB = 3x cm
- BC = 2x cm
- CD = 2(y + 1) cm = 2y + 2 cm
- AD = BC = 2x cm
- CD = AB = 3x cm
The perimeter (P) of a parallelogram is given by the formula:
P=2(AB+BC)
Substituting the values we have:
40=2(3x+2x)
Now we simplify the equation:
40=2(5x)
40=10x
To find x, divide both sides by 10:
x=4010
x=4
Now we know that AB = 3x and CD = 2y + 2. Since AB = CD:
3x=2y+2
Substituting the value of x:
3(4)=2y+2
12=2y+2
Now, isolate y:
12−2=2y
10=2y
y=102
y=5
Thus, the values are:
- x=4
- y=5
Topper's Solved these Questions
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - CONSTRUCTIONS OF POLYGONS
19 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - STATISTICS
2 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - MID-POINT THEOREM
12 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
Similar Questions
Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
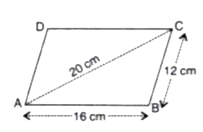
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionIn the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

View SolutionIn Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
View SolutionFind the perimeter of a parallelogram of a length 40cm and width 28 cm.
View SolutionIn parallelogram ABCD , AB = (3x- 4) cm, BC = ( y- 1) cm , CD = ( y+ 5) cm and AD = (2x+ 5) cm. find the ratio AB : BC.
Find the values of x and y.
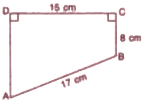
View SolutionThe given figure shows a trapezium ABCD in which AB = 17 cm, BC = 8 cm and CD = 15 cm. Find the area and perimeter of the trapezium.
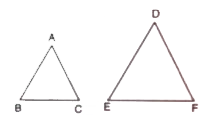
View Solution∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF
View SolutionIn the given figure, ΔABC is similar to ΔDEF,AB=(x−0.5) cm, AC=1.5xcm,DE=9cm,andDF=3xcm. Find the lengths of AB and DF.
View SolutionIn ΔABC,∠ABC=∠DAC,AB=8cm,AC=4cmandAD=5cm.

Find BC and CD.
View Solution
