The probability distribution function of a random variable X is given by Where . Find : (i) c (ii) (iii) .
To solve the given problem step by step, we will follow the instructions provided in the video transcript.
Step 1: Find the value of c
The probability distribution function is given as:
xi:012pi:3c34c−10c25c−1
Since the sum of all probabilities must equal 1, we can write the equation:
3c3+(4c−10c2)+(5c−1)=1
Simplifying this, we get:
3c3−10c2+9c−2=0
This is a cubic equation. We need to find the roots of this equation.
Step 2: Finding the roots of the cubic equation
Using the Rational Root Theorem or by trial and error, we can test possible rational roots. Testing c=1, c=2, and c=13:
1. For c=1:
3(1)3−10(1)2+9(1)−2=3−10+9−2=0(not valid since probabilities exceed 1)
2. For c=2:
3(2)3−10(2)2+9(2)−2=24−40+18−2=0(not valid since probabilities exceed 1)
3. For c=13:
3(13)3−10(13)2+9(13)−2=19−109+3−2=0(valid)
Thus, the valid value of c is:
c=13
Step 3: Calculate the probabilities p0,p1,p2
Using c=13:
1. p0=3c3=3(13)3=3⋅127=19
2. p1=4c−10c2=4(13)−10(13)2=43−109=12−109=29
3. p2=5c−1=5(13)−1=53−1=5−33=23
Step 4: Find P(X<2)
To find P(X<2):
P(X<2)=P(X=0)+P(X=1)=p0+p1=19+29=39=13
Step 5: Find P(1≤X≤2)
To find P(1≤X≤2):
P(1≤X≤2)=P(X=1)+P(X=2)=p1+p2=29+23=29+69=89
Summary of Results
1. c=13
2. P(X<2)=13
3. P(1≤X≤2)=89
3(1)3−10(1)2+9(1)−2=3−10+9−2=0(not valid since probabilities exceed 1)
3(2)3−10(2)2+9(2)−2=24−40+18−2=0(not valid since probabilities exceed 1)
3(13)3−10(13)2+9(13)−2=19−109+3−2=0(valid)
2. P(X<2)=13
3. P(1≤X≤2)=89
Topper's Solved these Questions
Similar Questions
The probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability distribution for a random variable X is as follows:
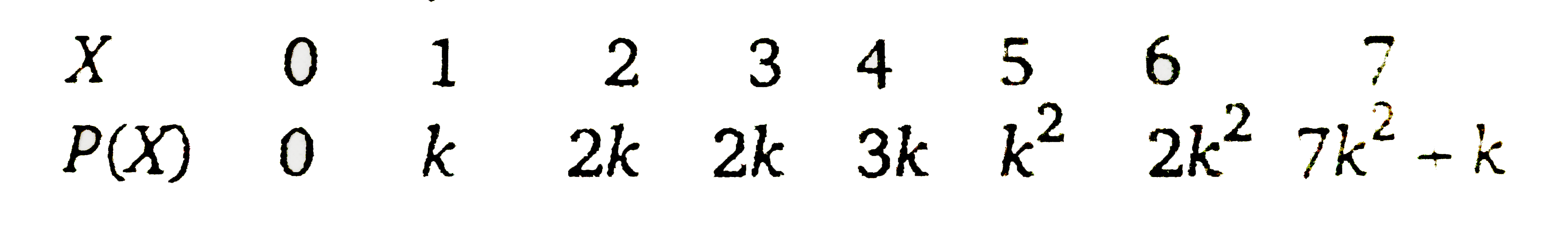
Find:
(i) k (ii) P(X<3) (iii) P(X>6)(iv)P(0X<3)
View SolutionThe probability function of a random variable X is given by
p(x)=13, if x = -1, 0, 1
=0, otherwise.
Find the distribution function of X.
View SolutionThe probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, is
View SolutionThe probability distribution of a random variable X is given below
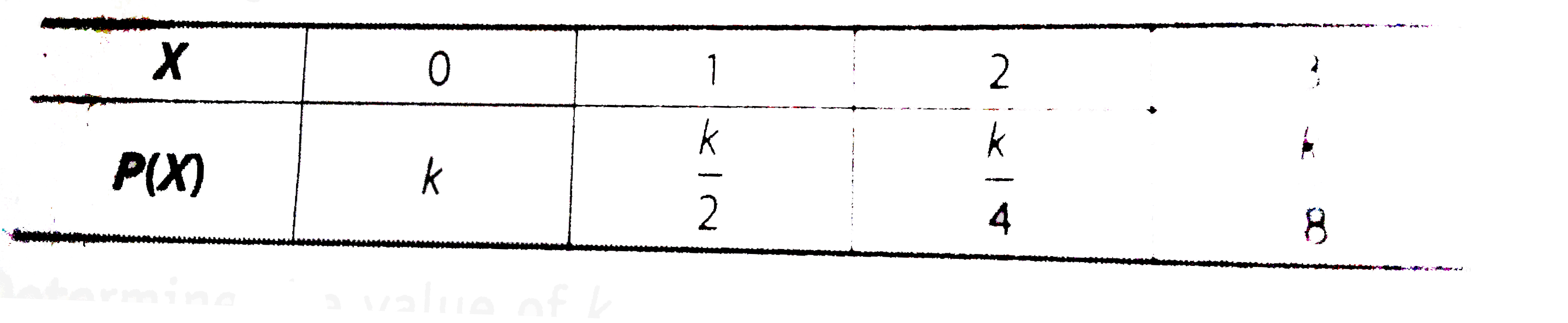
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).
View SolutionConsider the probability distribution of a random variable X

Calculate
(i) V(X2) (ii) Variance of X.
View SolutionIf the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionA probability distribution of a variable X is given below: X:01234 P(X):0.10.250.30.20.15 Find (i) Var(X) (ii) Var(X2)
View SolutionThe probability distribution of a discrete random variable x is given as under

Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.
View Solution
