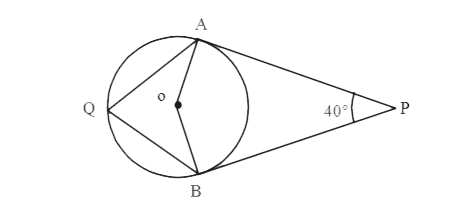
Theorem of angle between tangent and secant
If an angle has its vertex on the circle, its one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc .
Given : Let O be the centre of the circle. Line DBC is tangent to the circle at point B. Seg BA is a chord of the circle. Point X of the circle is on C side of line BA and point Y of the circle is on D side of line BA.
To prove : m ∠ABC=12m(arcAXB).
Video Solution
Text Solution
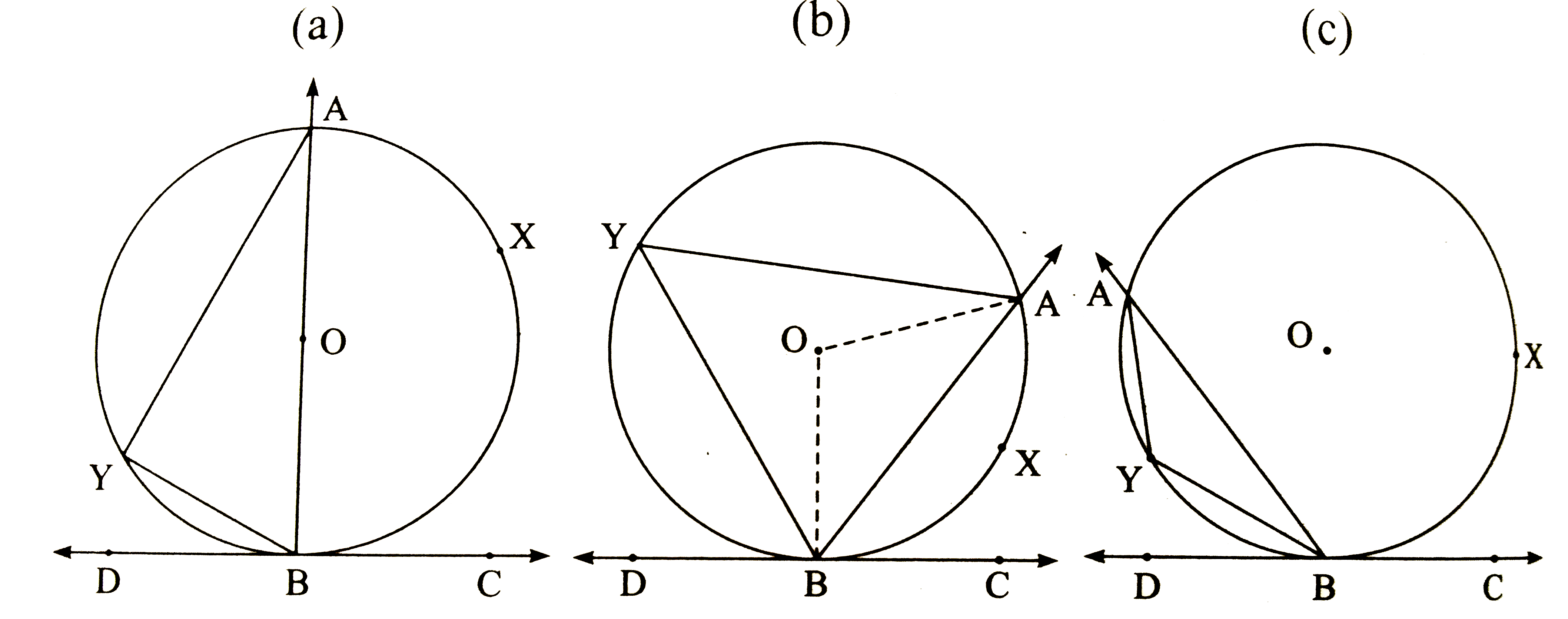
Proof : Considering ∠ABC and the arc AXB intercepted by it, we see from the figures that arc AXB may be a semicircle, may be a minor arc or may be a major arc. We deal with these cases separately .
(a) When ∠ABC intercepts a semicircle , [as in figure (a) ] the chord BA passes through the centre.
In that case, ∠ABC=90∘ ....(Tangent theorem )
Also since m ( arc BXA =180∘
∴12m (arc BXA ) =12×180∘=90∘
∴ m ∠ABC=12m (arc BXA )
(b) When ∠ABC intercepts a minor arc, [ as in figure (b) ] the centre lies in the exterior of ∠ABC.
We have ,m∠ABC=90∘−m∠ABO
∴m∠ABO=90∘−m∠ABC
∴m∠BAO=90∘−m∠ABC ....(ΔABC is isosceles )
m∠ABO+m∠BAO=180∘−2m∠ABC
∴180∘−m∠BOA=180∘−2m∠ABC
∴180∘−m∠BOA=180∘−2m∠ABC
∴m∠BOA=2m∠ABC
But m∠BOA=m(arcAXB)
∴m∠ABC=12m (arc AXB)
(c) When ∠ABC intercepts a major arc [as in figure (c ) the centre lies in the interior of ∠ABC .
We then have ∠DBA intercepting a minor arc BYA .
∴m∠DBA=12 m (arc BYA )
∴180∘−m∠ABC=12[360∘−m (arc AXB ) ]
=180∘−12 m (arc AXB )
∴m∠ABC=12 m (arc AXB )
Thus, in every case we have shown that m∠ABC=12 m (arc AXB ) .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - PYTHAGORAS THEOREM4videos
THEOREMS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRYEXERCISE - CHALLENGING QUESTIONS6videos
TRIGONOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
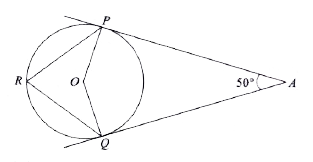 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘ - Question 2 - Select One
The radian measure of the angle, subtends at the centre of a circle by an arc whose length is twice the diameter of the circle, is
A2Bπ2CπD4 - Question 3 - Select One
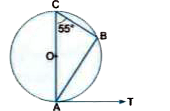
In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
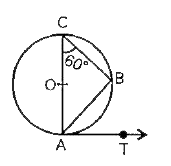 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘
In Fig O is the centre of a circle and AT is a tangent at point A . what is the measure of ∠BAT ?
 View Solution
View SolutionThe length of a minor arc is 29 of the circumference of the circle. Write the measure of the angle (in degrees) subtended by the arc at the centre of the circle.
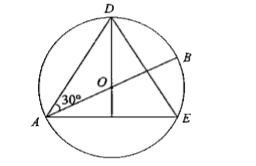
View SolutionIn the given figure, O is the centre of the circle. Then ∠AED measure
 View Solution
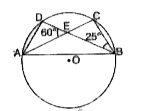
View SolutionIn the given figure, O is the centre of the circle. The measure of ∠ ADB is
 View Solution
View SolutionThe tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
View Solution