Two circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
The correct Answer is:90∘
To prove that the center-line AB bisects the common chord PQ perpendicularly, we can follow these steps:
Step 1: Draw the Circles and Label the Points
- Draw two circles with centers A and B that intersect at points P and Q.
- Label the points of intersection as P and Q.
Hint: Start by visualizing the two circles and their intersection points.
Step 2: Draw the Line Segment AB
- Draw the line segment connecting the centers A and B.
- Let this line segment intersect the chord PQ at point M.
Hint: Ensure that M is the point where line AB crosses the line segment PQ.
Step 3: Join Relevant Points
- Join points P and B, and points Q and B.
- Also, join points A and P, and points A and Q.
Hint: This will help in forming triangles that we can analyze.
Step 4: Identify the Triangles
- Consider triangles BPM and BQM.
Hint: Look for properties of these triangles that can help in proving congruence.
Step 5: Show that BP = BQ
- Since both BP and BQ are radii of the circle centered at B, we have BP = BQ.
Hint: Remember that the radii of a circle are equal.
Step 6: Show that Angles BPM and BQM are Equal
- The angles BPM and BQM are equal because they are angles subtended by the same chord PQ from point B.
Hint: Think about the properties of angles in circles.
Step 7: Show that PM = QM
- Since M is the point where line AB intersects PQ, we need to show that PM = MQ.
- Note that in triangles BPM and BQM, we have two sides equal (BP = BQ) and the angle between them is equal (angle BPM = angle BQM).
Hint: Use the Side-Angle-Side (SAS) congruence criterion to establish this.
Step 8: Conclude that M is the Midpoint of PQ
- By the congruence of triangles BPM and BQM, we can conclude that PM = MQ.
- Therefore, M is the midpoint of PQ.
Hint: This midpoint property is crucial for the next step.
Step 9: Show that AB is Perpendicular to PQ
- Since M is the midpoint and AB intersects PQ at M, we need to show that AB is perpendicular to PQ.
- In triangles APM and AQB, we can use the fact that both triangles share side AM and have equal angles at M.
Hint: Look for right angles in the triangles formed.
Step 10: Conclude the Proof
- Since M is the midpoint of PQ and AB intersects PQ at M, we conclude that line AB bisects PQ perpendicularly.
Hint: Summarize the findings to reinforce the conclusion.
Final Conclusion
Thus, we have proved that the center-line AB bisects the common chord PQ perpendicularly.
- Draw two circles with centers A and B that intersect at points P and Q.
- Label the points of intersection as P and Q.
- Draw the line segment connecting the centers A and B.
- Let this line segment intersect the chord PQ at point M.
- Join points P and B, and points Q and B.
- Also, join points A and P, and points A and Q.
- Consider triangles BPM and BQM.
- Since both BP and BQ are radii of the circle centered at B, we have BP = BQ.
- The angles BPM and BQM are equal because they are angles subtended by the same chord PQ from point B.
- Since M is the point where line AB intersects PQ, we need to show that PM = MQ.
- Note that in triangles BPM and BQM, we have two sides equal (BP = BQ) and the angle between them is equal (angle BPM = angle BQM).
- By the congruence of triangles BPM and BQM, we can conclude that PM = MQ.
- Therefore, M is the midpoint of PQ.
- Since M is the midpoint and AB intersects PQ at M, we need to show that AB is perpendicular to PQ.
- In triangles APM and AQB, we can use the fact that both triangles share side AM and have equal angles at M.
- Since M is the midpoint of PQ and AB intersects PQ at M, we conclude that line AB bisects PQ perpendicularly.
Thus, we have proved that the center-line AB bisects the common chord PQ perpendicularly.
Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(A)
14 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
Two circles with centres O and O'are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. prove that OA bisects angle BAC.

View SolutionIn the figure, PO⊥QO. The tangents to the circle with centre O at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.

View SolutionIf two circles touching both the axes intersect at two points P and Q where P=(3,1) then PQ=
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionIf two circles intersect in two points, prove that the line through the centres is the perpendicular bisector of the common chord.
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

View SolutionTwo parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
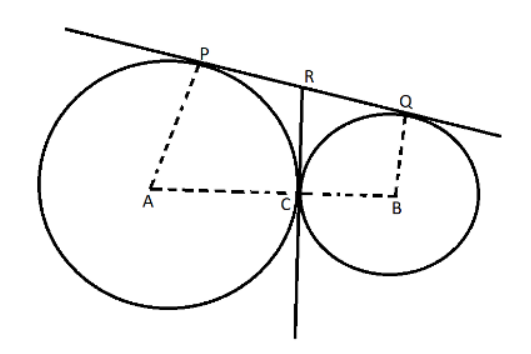
View SolutionIf a number of circles pass through the end points P and Q of a line segment PQ, then Prove that their centres lie on the perpendicular bisector of PQ.
View Solution
