Two equal circles intersect in and . A straight line through meets the circles in and . Prove that
As we know that the two circles will congruent if they have equal radii.
Also, we know that if two chords are equal then the corresponding arcs are congruent.
Since, PQ is the common chord in both the circles.
So their corresponding arcs are equal.
arc PCQ=arc PDQ
Now, the congruent arcs have the same degree
the base angles of an isosceles triangle are equal
Topper's Solved these Questions
Similar Questions
Two equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View Solution
Knowledge Check
- Question 1 - Select One
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘
Two circles of equal radii cut each other at P and Q, so that the centre of one lies on the other. A straight line through P cuts the circle again at A and B. Prove that ΔQAB is equilateral triangle.
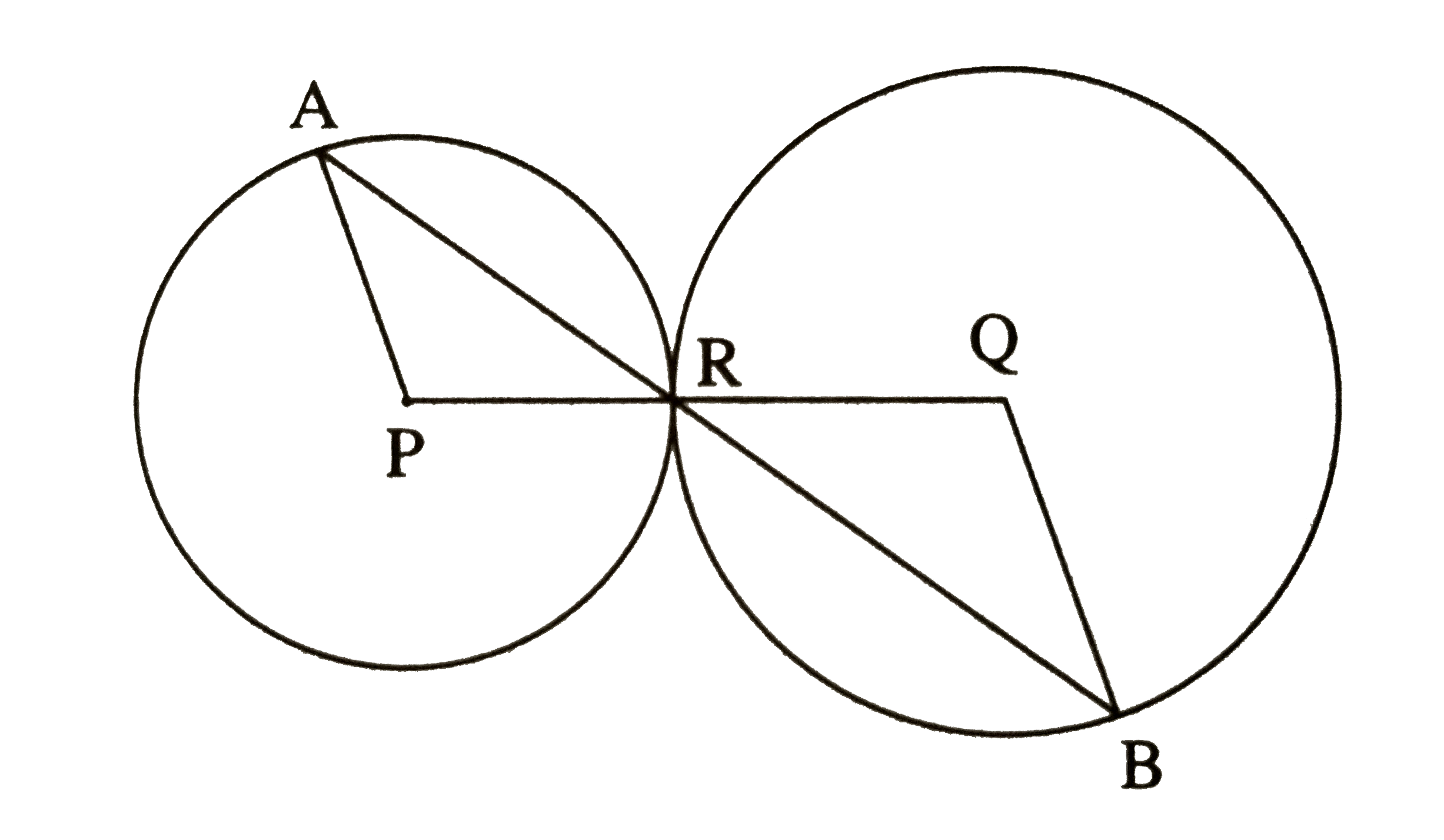
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
seg AP || seg BQ
 View Solution
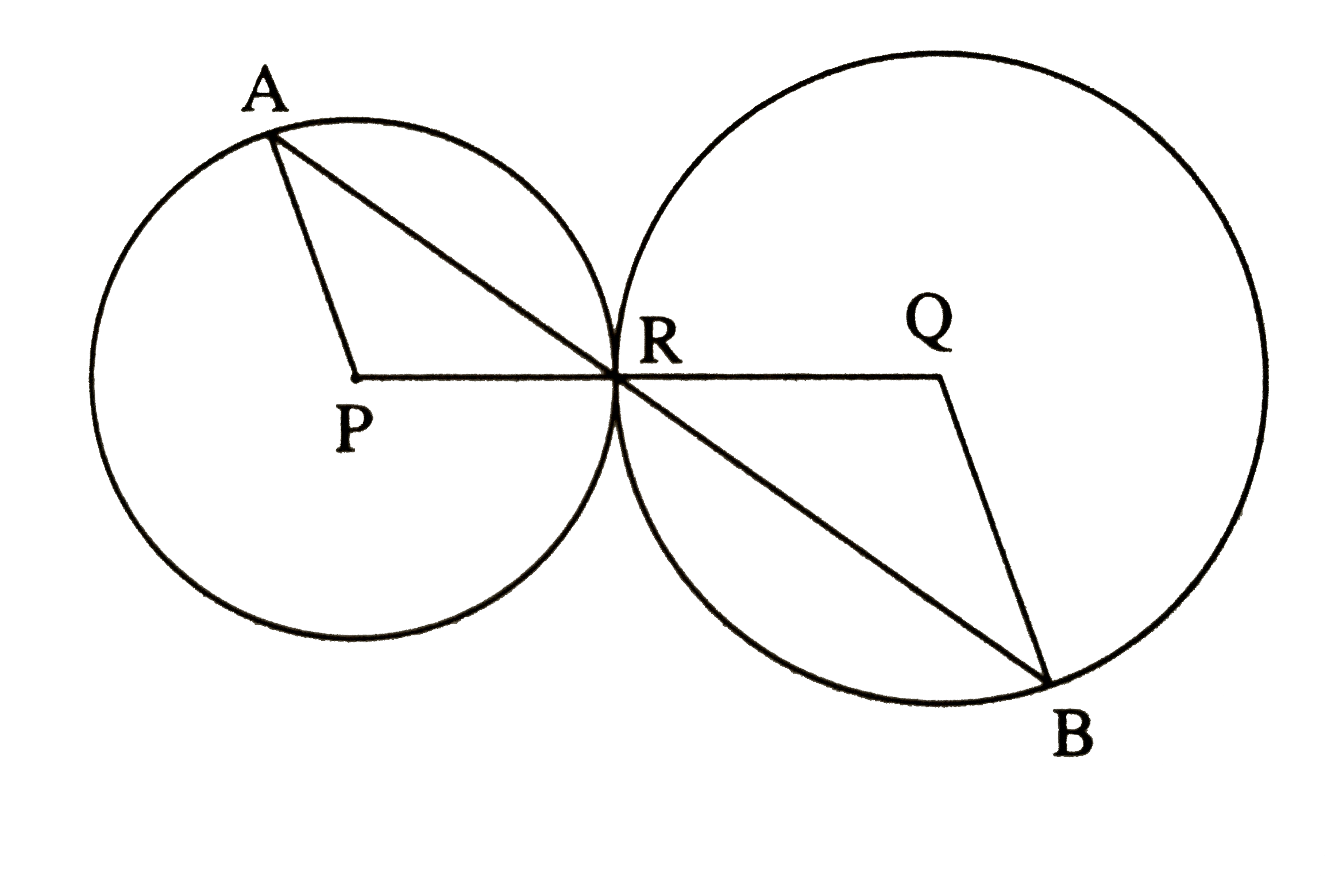
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
△APR~△RQB
 View Solution
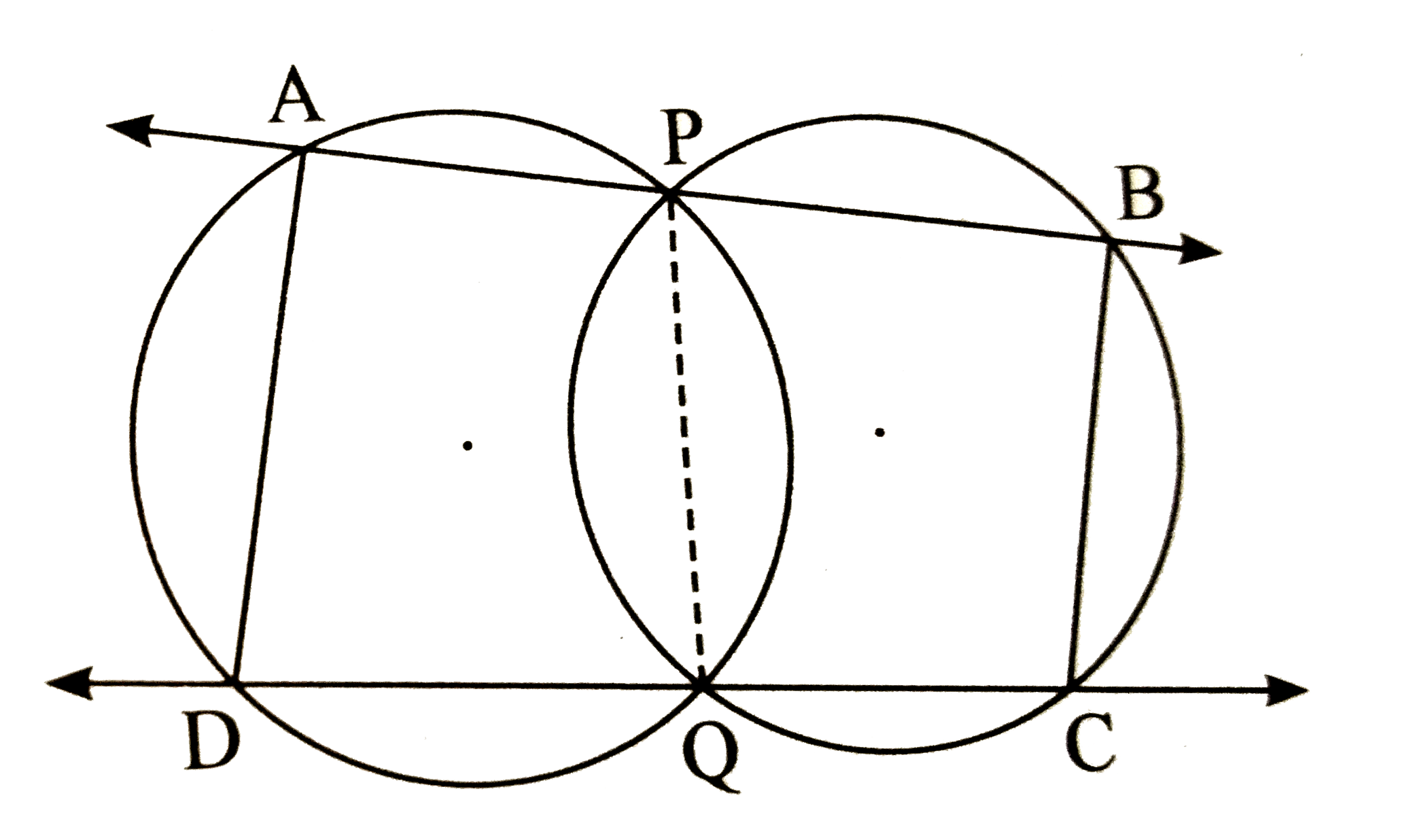
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
 View Solution
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
 View Solution
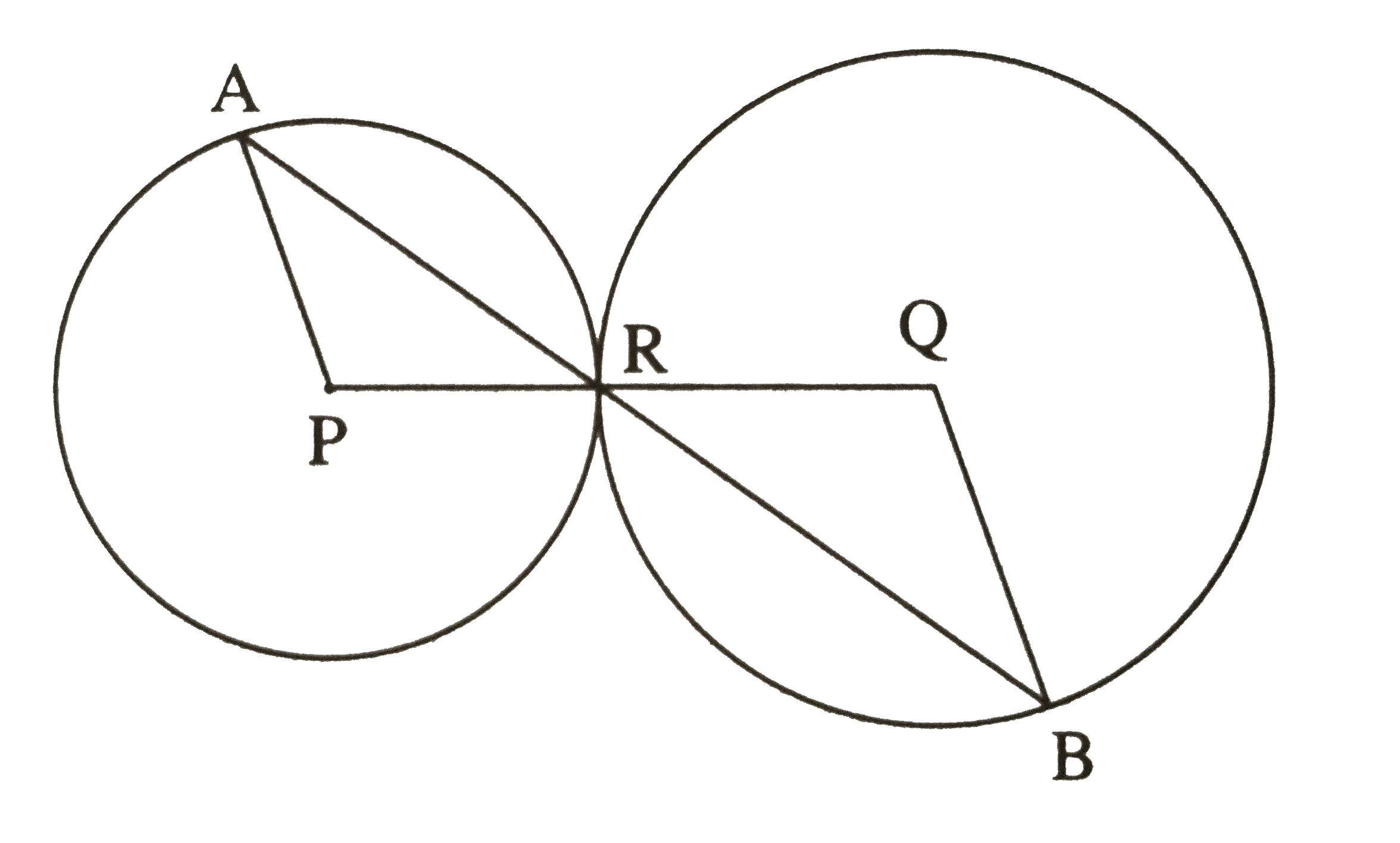
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively.
Find ∠RQB if ∠PAR=35∘
 View Solution
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.
 View Solution
View Solution

