Question

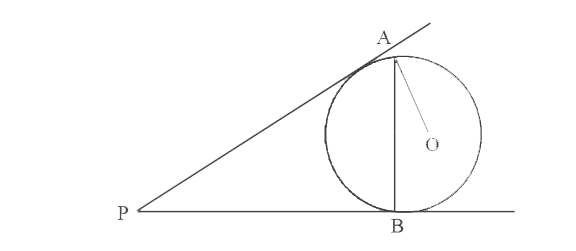
Two
tangents $TP$
and $TQ$
are drawn
to a circle with centre $O$
from an
external point $T$
. Prove
that $\angle PTQ=2\angle OPQ$
.

Explanation

To prove that $$\angle PTQ=2\angle OPQ$$, we will follow these steps:

Step 1: Identify the given elements
We have a circle with center \(O\) and an external point \(T\) from which two tangents \(TP\) and \(TQ\) are drawn to the circle.

Step 2: Establish the right angles
Since \(TP\) and \(TQ\) are tangents to the circle at points \(P\) and \(Q\), we know that:
\( \angle OPT = 90^\circ \quad \text{and} \quad \angle OQT = 90^\circ \)
This is because the radius at the point of tangency is perpendicular to the tangent line.

Step 3: Use the property of tangents
From the external point \(T\), the lengths of the tangents to the circle are equal:
\( TP = TQ \)
This means that triangle \(TPQ\) is an isosceles triangle.

Step 4: Establish angles in triangle \(TPQ\)
In triangle \(TPQ\), since \(TP = TQ\), we have:
\( \angle TPQ = \angle TQP \)
Let us denote these angles as \(x\). Therefore, we can write:
\( \angle PTQ = x + x = 2x \)

Step 5: Apply the triangle angle sum property
The sum of angles in triangle \(TPQ\) is \(180^\circ\):
\( \angle PTQ + \angle TPQ + \angle TQP = 180^\circ \)
Substituting the known angles, we have:
\( 2x + x + x = 180^\circ \)
This simplifies to:
\( 2x + 2x = 180^\circ \implies 4x = 180^\circ \implies x = 45^\circ \)
Thus, we find:
\( \angle PTQ = 2x = 90^\circ \)

Step 6: Relate angles \(OPQ\) and \(PTQ\)
Now, consider triangle \(OPQ\):
Since \(OP\) and \(OQ\) are radii of the circle, we have:
\( \angle OPQ + \angle OQP + \angle POQ = 180^\circ \)
Since \(\angle OPQ = \angle OQP\) (both are equal as they are opposite the equal sides \(OP\) and \(OQ\)), let’s denote them as \(y\):
\( y + y + \angle POQ = 180^\circ \)
Now, we know that:
\( \angle POQ = 90^\circ \quad (\text{as it is the angle subtended by the tangents}) \)
Thus:
\( 2y + 90^\circ = 180^\circ \implies 2y = 90^\circ \implies y = 45^\circ \)
Therefore:
\( \angle OPQ = 45^\circ \)

Step 7: Final relationship
Now we can conclude:
\( \angle PTQ = 2 \times \angle OPQ \)
Substituting the values we found:
\( 90^\circ = 2 \times 45^\circ \)
Thus, we have proved that:
\( \angle PTQ = 2\angle OPQ \)