Which of the following is highest?
$(a) cosec 1 (b) cosec 2$
$(c) cosec 4 (d) cosec (- 6)$

Video Solution

Text Solution

Verified by Experts

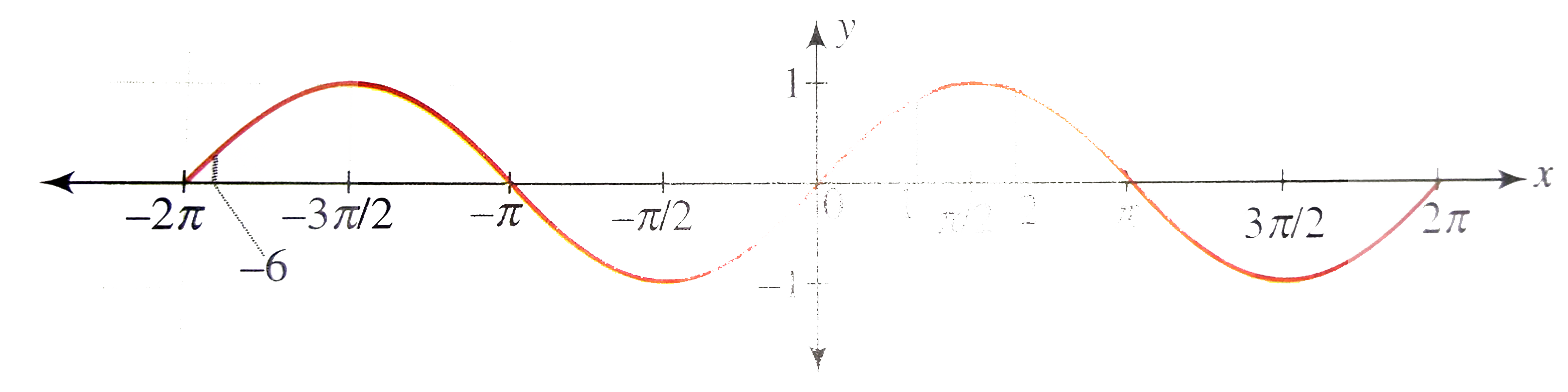
Consider sin 1, sin 2 and -sin 6 (sin 4 is negative, hence cosec 4 cannot be maximum).
Form the graph, sin (-6) is the least positive value, hence cosesc (-6) is maximum.

Updated on:21/07/2023

$cos e c 48^{\circ} + cos e c 96^{\circ} + cos e c 192^{\circ} + cos e c 384^{\circ} =$
A $4 \sqrt{3}$
B0
C $- 4 \sqrt{3}$
D $1$
If $a_{1}, a_{2}, \dots \dots . . a_{n}$ are in A.P. with common difference d, then the sum of these series
$sin d [{cosec a}_{1} {cosec a}_{2} + {cosec a}_{2} {cosec a}_{3} + ... ... + ... ... . + {cosec a}_{n - 1} - {cosec a}_{n}]$
A ${sec a}_{1} - {sec a}_{n}$
B ${cosec a}_{1} - {cosec a}_{n}$
C ${cot a}_{1} - {cot a}_{n}$
D ${tan a}_{1} - {tan a}_{n}$