Write a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.Solution in Bengali
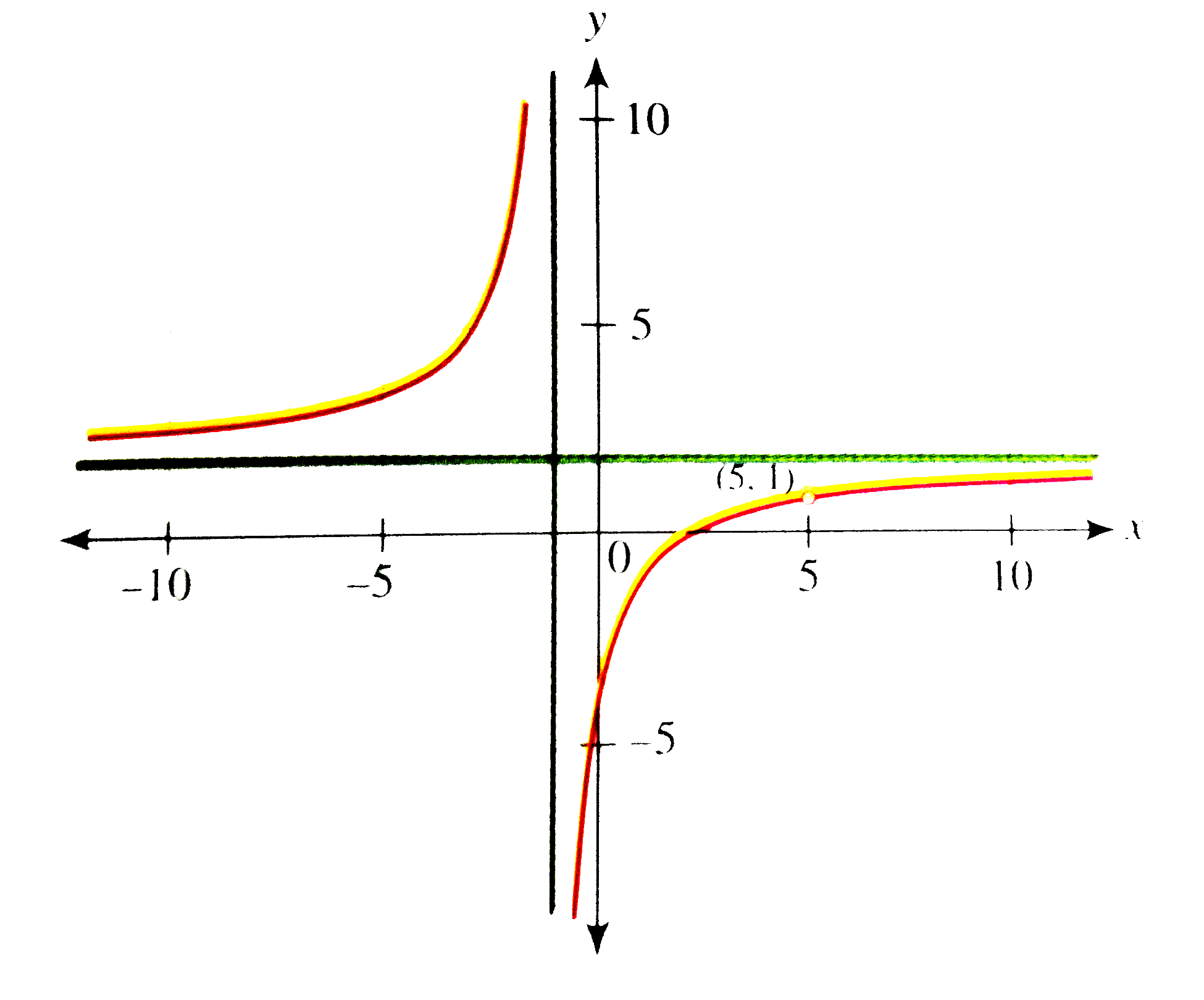
Since h has a hole at x = 5 , both the numerator and the denominator have a zero at x = 5. Also the vertical asymptote at at x = -1 means the denominator has a zero at x = -1. An x-intercept at x = 2 means the numerator has a zero at x = 2 . Finally, the horizontal asymptote y = 2 means that the numerator and the denominator have equal degree and the ratio of their leading coefficients is equal to 2. Hence
h(x)=2(x−5)(x−2)(x−5)(x+1)
The graph of h is shown below, check the characteristics.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION78videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
01:58View SolutionPlot y=|x|,y+x−2∣,andy=|x|2∣
01:55View SolutionDraw the graph of y=1(1/x).
View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?01:52View SolutionWrite a possible rational function h with a hole at x = 5, a vertical asymptote at x = -1, a horizontal asymptote at y = 2 and x-intercept at x = 2.
05:29View SolutionWrite a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
05:31View SolutionWrite a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
02:56View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
03:11View SolutionWhat is the equation of the horizontal asymptote of the function f(x)=(2x−1)(x+3)(x+3)2?
02:12View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?06:36View SolutionWrite a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
02:21View SolutionWrite a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
02:34View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
03:06View SolutionFind the asymptotes, intercepts and sketch the graph the function f(x)=x2−x−6x−3
04:54View SolutionFind the asymptotes, intercepts and sketch the graph of the function f(x)=x2−4x3−4x2
03:21View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?04:43View Solution

