Complete Solutions to EXERCISE 15(C) of chapter SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) |
| SELINA PUBLICATION | EXERCISE 15(C) |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
View SolutionAreas of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
View SolutionA line PQ is drawn parallel to the base BC of `Delta ABC ` which meets sides AB and AC at points P and Q respectively. If `AP = 1/3 PB`, find the value of :
`("Area of " Delta ABC)/("Area of "Delta APQ)`
View SolutionA line PQ is drawn parallel to the base BC of `Delta ABC ` which meets sides AB and AC at points P and Q respectively. If `AP = 1/3 PB`, find the value of :
`("Area of " Delta APQ)/("Area of trapezium"PBCQ)`
View SolutionThe perimeters of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
View SolutionIn the given figure, `AX : XB = 3:5`

Find :
the length of BC, if the length of XY is 18 cm.
View SolutionIn the given figure, `AX : XB = 3:5`

Find :
the ratio between the areas of trapezium XBCY and triangle ABC.
View SolutionABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQI/ BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP: AB.
View SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.
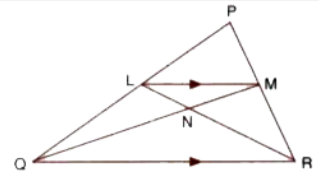
Calculate the value of ratio :
`(PL)/(PQ)` and then `(LM)/(QR)`
View SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.

Calculate the value of ratio :
`("Area of "DeltaLMN)/("Area of "Delta MNR")`
View SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.

Calculate the value of ratio :
`("Area of "DeltaLQM)/("Area of" DeltaLQN)`
View SolutionThe given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel, PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ. Calculate :
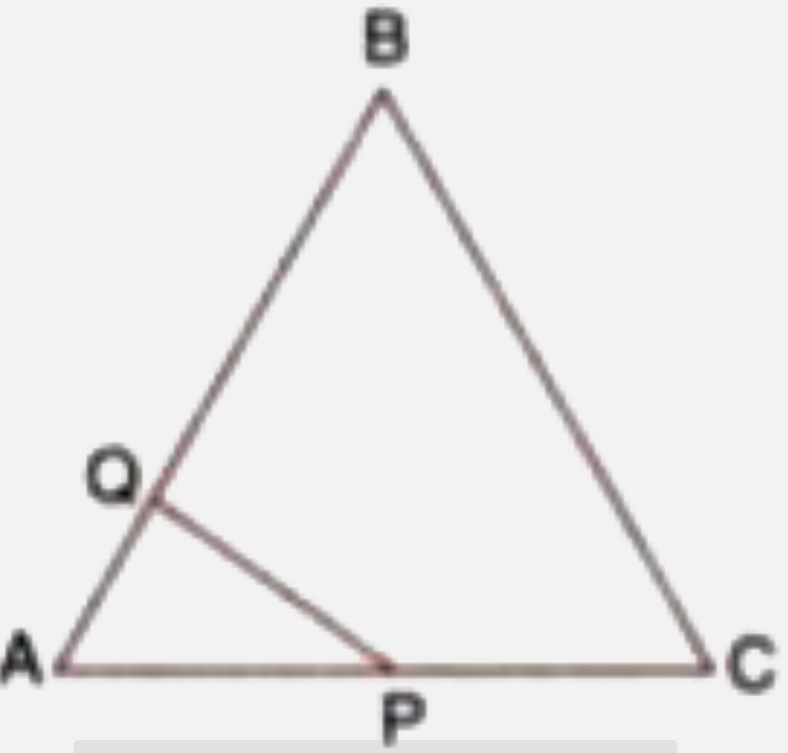
the length of AP.
View SolutionThe given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel, PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ. Calculate :

the ratio of the areas of triangle APQ and triangle ABC.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle `CPQ = 20 cm^2`
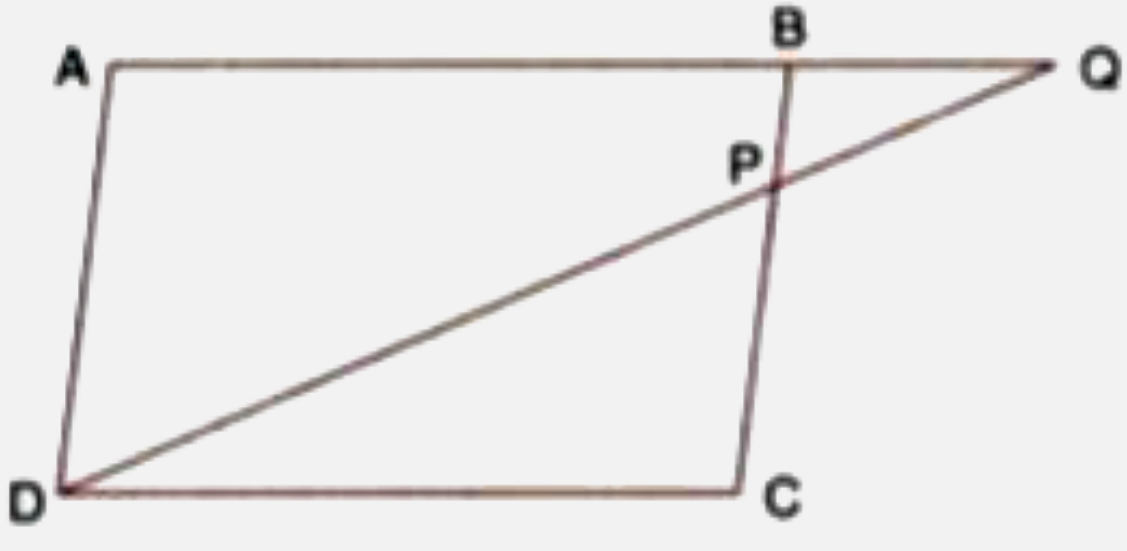
Calculate :
area of triangle CDP.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle `CPQ = 20 cm^2`

Calculate :
area of parallelogram ABCD.
View SolutionIn the given figure, BC is parallel to DE. Area of triangle `ABC = 25 cm^2`, Area of trapezium `BCED = 24 cm^2 and DE = 14 cm`. Calculate the length of BC.
Also, find the area of triangle BCD.
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
`DeltaAPB : DeltaCPB`
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,
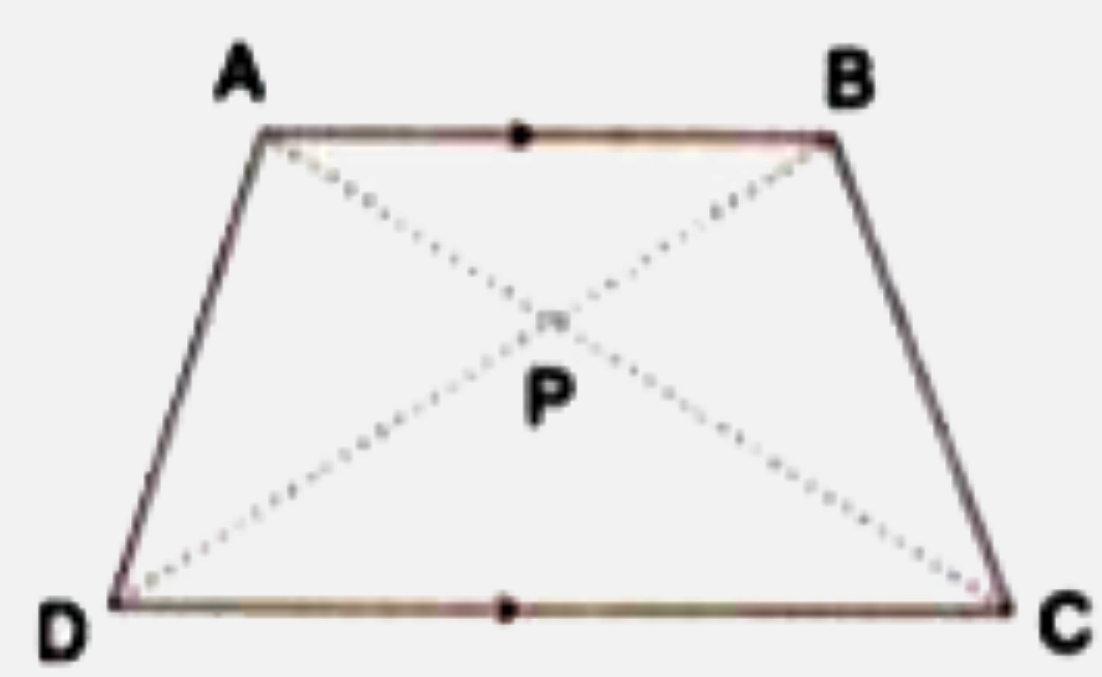
Find :
`DeltaDPC : DeltaAPB`
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
`DeltaADP : Delta APB`
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
`DeltaAPB : DeltaADB`
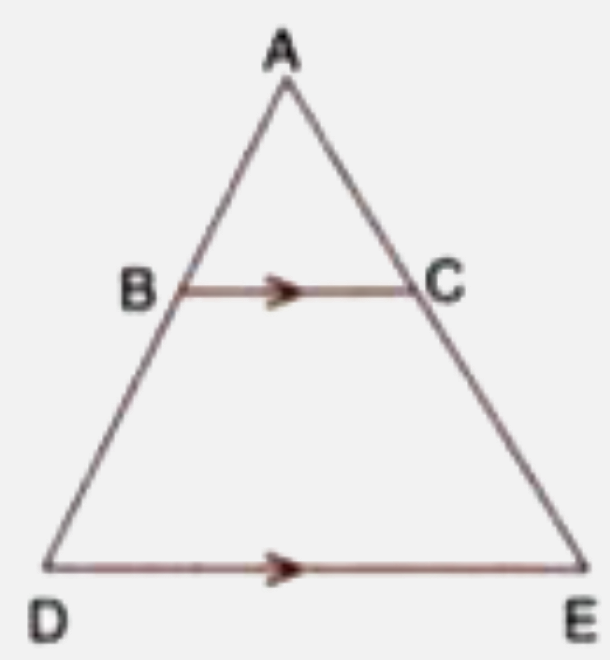
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`

Determine the ratios and `(AD)/(AB)`
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`

Prove that `DeltaDEF` is similar to `DeltaCBF`.Hence, find `(EF)/(FB)`.
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`

What is the ratio of the areas of `Delta DEF` and `Delta BFC` ?
View SolutionIn the given figure, `/_B = /_E, /_ACD = /_BCE, AB = 10.4` cm and `DE = 7.8 cm`. Find the ratio between areas of the `Delta ABC and Delta DEC`.
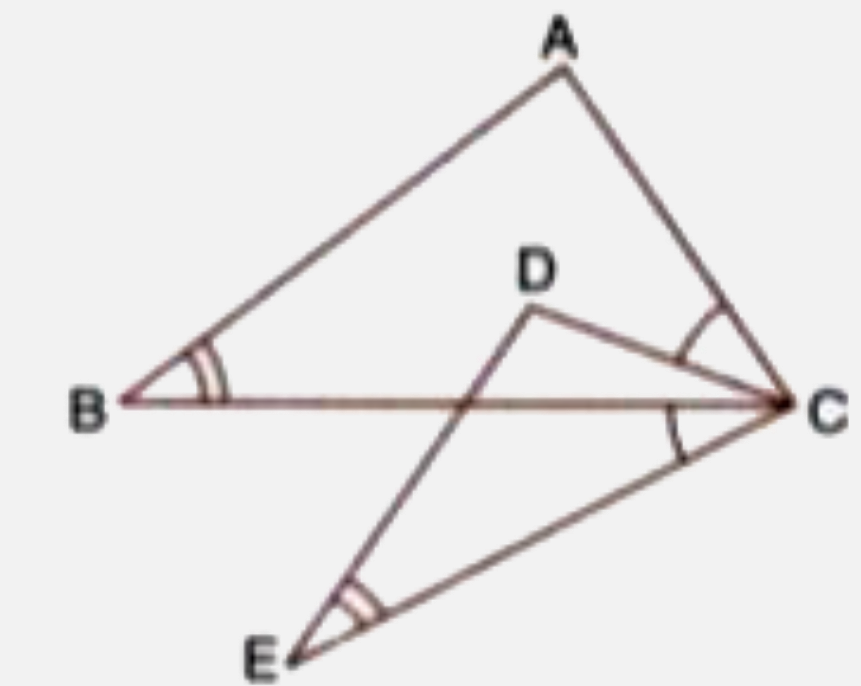
View Solution
EXERCISE 15(C) questions and complete solutions for chapter SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) of SELINA MATHS (ENGLISH) of Class 10