Complete Solutions to QUESTIONS of chapter SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
In the given figure, `DeltaABC ` is similar to `Delta DEF, AB = (x - 0.5)` cm, `AC = 1.5x cm, DE = 9 cm, and DF = 3x cm`. Find the lengths of AB and DF.
View SolutionIn the given figure, AP = 8 cm, BP = 22 cm, AQ = 12 cm and QC = 8 cm

Show that `DeltaAPQ ` is similar to `DeltaACB`.
View SolutionIn the given figure, AP = 8 cm, BP = 22 cm, AQ = 12 cm and QC = 8 cm

If PQ = 14 cm, find BC.
View SolutionTheorem 6.7 : If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
View SolutionIn the given figure, lines l and m are parallel. Three concurrent lines through point O meet line l at points A, B and C, and line m at points P, Q and R as shown. Prove that : `(AB)/(BC) = (QR)/(PQ)`

View SolutionIn the figure, given alongside, `/_QPS = /_RPT `
and `/_PRQ = /_PTS`.

Prove that triangles PQR and PST are similar.
View SolutionIn the figure, given alongside, `/_QPS = /_RPT `
and `/_PRQ = /_PTS`.

If PT : ST = 3:4, find the ratio between QR : PR.
View SolutionIn the given figure, AB and DE are perpendiculars to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.

View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
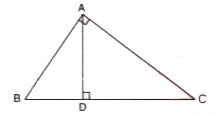
Prove that : `Delta ABD ` is similar to `DeltaCAD`.
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.

If BD = 3.6 cm and CD = 6.4 cm, find the length of AD.
View SolutionIn the adjoining figure, `DE////BC ` and D divides AB in the ratio 2 : 3. Find :

`(AE)/(EC)`
View SolutionIn the adjoining figure, `DE////BC ` and D divides AB in the ratio 2 : 3. Find :
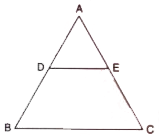
`(AE)/(AC)`
View SolutionIn the adjoining figure, `DE////BC ` and D divides AB in the ratio 2 : 3. Find DE, if BC = 7.5 cm.
View SolutionIn `DeltaABC`, D and E are points on the sides AB and AC respectively. Find whether DE//BC, if :
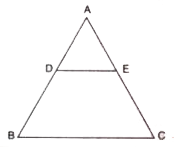
`AD = 3 cm ," " BD = 4.5 cm, AE = 4 cm " and " AC = 10 cm `
View SolutionIn `DeltaABC`, D and E are points on the sides AB and AC respectively. Find whether DE//BC, if :
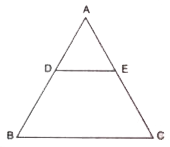
`AD = 7 cm, " " BD = 45 cm, AE = 35 cm " and " CE = 56 cm`
View SolutionIn the given figure, AB//EF//CD. Given that AB = 7.5 cm, EG = 2-5 cm, GC = 5 cm and DC = 9 cm. Calculate :

EF
View SolutionIn the given figure, AB//EF//CD. Given that AB = 7.5 cm, EG = 2-5 cm, GC = 5 cm and DC = 9 cm. Calculate :

AC.
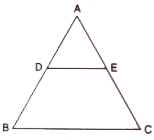
View SolutionIn the given figure, DE // BC.

Prove that `Delta ADE and Delta ABC ` are similar
View SolutionIn the given figure, DE // BC.
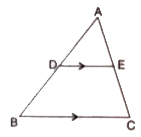
Given that `AD = 1/2 BD`, calculate DE, if BC = 45 cm.
Also , find `(Ar. (Delta ADE))/(Ar. (DeltaABC)) and (Ar.(DeltaADE))/(Ar.("trapezium BCED"))`
View SolutionIn the figure, given alongside, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and area of `Delta POB - 120 cm^2`. find the area of `Delta QOA`.

View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 3. Find the ratio :
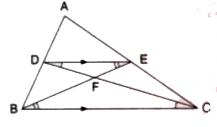
`(AD)/(AB)` and then `(DE)/(BC)`
View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio :

`("Area of "DeltaDEF)/("Area of"Delta BFC)`
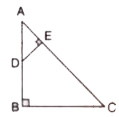
View SolutionIn `Delta ABC, /_B = 90^@, AB = 12 cm and AC = 15 cm`. D and E are points on AB and AC respectively such that `/_AED = 90^@` and DE = 3 cm. Calculate the area of `Delta ABC` and then the area of `Delta ADE.`
View SolutionA model of a ship is made to a scale of 1:200. If the length of the model is 4 m, calculate the length of the ship.
View SolutionThe scale of map is 1 : 50,000. In the map, a triangular plot ABC of land has the following dimensions :
`AB = 2 cm, BC = 3.5 cm ` and angle `ABC = 90^@`.
Calculate : the actual length of side BC, in km, of the land.
View SolutionThe scale of map is 1 : 50,000. In the map, a triangular plot ABC of land has the following dimensions :
`AB = 2 cm, BC = 3-5 cm ` and angle `ABC = 90^@`.
Calculate : the area of the plot in sq. km.
View SolutionA rectangular tank has length = 4 m, width = 3 m and capacity = `30 m^3`. A small model of the tank is made with capacity `240 cm^3`. Find :
the dimensions of the model.
View SolutionA rectangular tank has length = 4 m, width = 3 m and capacity = `30 m^3`. A small model of the tank is made with capacity `240 cm^3`. Find :
the ratio between the total surface area of the tank and its model.
View Solution
QUESTIONS questions and complete solutions for chapter SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) of SELINA MATHS (ENGLISH) of Class 10