Complete Solutions to EXERCISE 15(A) of chapter SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) |
| SELINA PUBLICATION | EXERCISE 15(A) |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
In the figure, given below, straight lines AB and CD intersect at P, and AC//BD. Prove that :

`Delta APC and DeltaBPD ` are similar.
View SolutionIn the figure, given below, straight lines AB and CD intersect at P, and AC//BD.

If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm, find the lengths of PA and PC.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
`DeltaAPB ` is similar to `DeltaCPD`.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
`PA xx PD = PB xx PC`.
View SolutionP is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
`DP : PL = DC : BL`.
View SolutionP is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
`DL : DP = AL : DC`
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
`DeltaAOB ` is similar to `DeltaCOD`.
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
`OA xx OD = OB xx OC`.
View SolutionIn `DeltaABC`, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
`CB : BA = CP : PA`
View SolutionIn `DeltaABC`, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
`AB xx BC = BP xx CA`
View SolutionIn `DeltaABC, BM _|_ AC and CN _|_ AB`, show that :
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
View SolutionIn the given figure, `DE////BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm`.
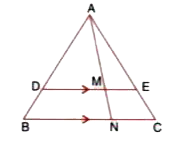
Write all possible pairs of similar triangles.
View SolutionIn the given figure, `DE////BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm`.
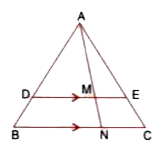
Find lengths of ME and DM.
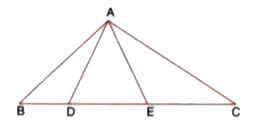
View SolutionIn the given figure, AD = AE and `AD^2 = BD xx EC`.
Prove that : triangles ABD and CAE are similar.
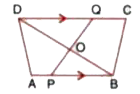
View SolutionIn the given figure, `AB////DC, BO = 6 cm ` and `DQ = 8 cm`, find: `BP xx DO`.
View SolutionAngle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm, find the length of PB.
View SolutionState, true or false :
Two similar polygons are necessarily congruent.
View SolutionState, true or false :
Two congruent polygons are necessarily similar.
View SolutionState, true or false :
All equiangular triangles are similar.
View SolutionState, true or false :
All isosceles triangles are similar.
View SolutionState, true or false :
Two isosceles-right triangles are similar.
View SolutionState, true or false :
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
View SolutionState, true or false :
The diagonals of a trapezium divide each other into proportional segments.
View SolutionGiven : `/_GHE = /_DFE = 90^@`,
`DH = 8, DF = 12`,
`DG = 3x - 1 and DE = 4x + 2`.
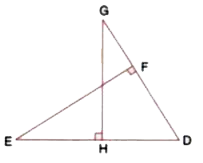
Find : the lengths of segments DG and DE.
View SolutionD is a point on the side BC of a triangle ABC such that `/_A D C=/_B A C`. Show that `C A^2=C BdotC D`.
View SolutionIn the given figure, `DeltaABC ` and `DeltaAMP` are right angled at B and M respectively.
Given `AC = 10 cm, AP = 15 cm and PM = 12 cm`.

Prove that : `DeltaABC - DeltaAMP `
View SolutionIn the given figure, `DeltaABC ` and `DeltaAMP` are right angled at B and M respectively.
Given `AC = 10 cm, AP = 15 cm and PM = 12 cm`.
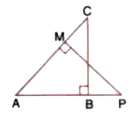
Find : AB and BC.
View SolutionGiven : RS and PT are altitudes of `DeltaPQR`. Prove that:
`Delta PQT ~ Delta QRS`.
View SolutionGiven : RS and PT are altitudes of `DeltaPQR`. Prove that:
`PQ xx QS = RQ xx QT`.
View SolutionGiven : ABCD is a rhombus, DPR and CBR are straight lines.
Prove that : ` DP xx CR = DC xx PR`.
View SolutionGiven : `FB = FD, AE _|_ FD and FC _|_ AD`.
Prove that: : `(FB)/(AD) = (BC)/(ED)`
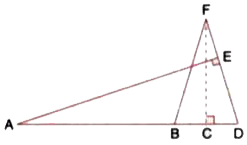
View SolutionIn `DeltaPQR, /_Q = 90^@` and QM is perpendicular to PR. Prove that :
`PQ^2 = PM xx PR`
View SolutionIn `DeltaPQR, /_Q = 90^@` and QM is perpendicular to PR. Prove that :
`QR^2 = PR xx MR`
View SolutionIn `DeltaPQR, /_Q = 90^@` and QM is perpendicular to PR. Prove that :
`PQ^2 + QR^2 = PR^2`
View SolutionIn `Delta ABC, /_B = 90^@` and `BD _|_ AC`.
If CD = 10 cm and BD = 8 cm, find AD.
View SolutionIn `Delta ABC, /_B = 90^@` and `BD _|_ AC`.
If AC = 18 cm and AD = 6 cm, find BD.
View SolutionIn `Delta ABC, /_B = 90^@` and `BD _|_ AC`.
If AC = 9 cm and AB = 7 cm, find AD.
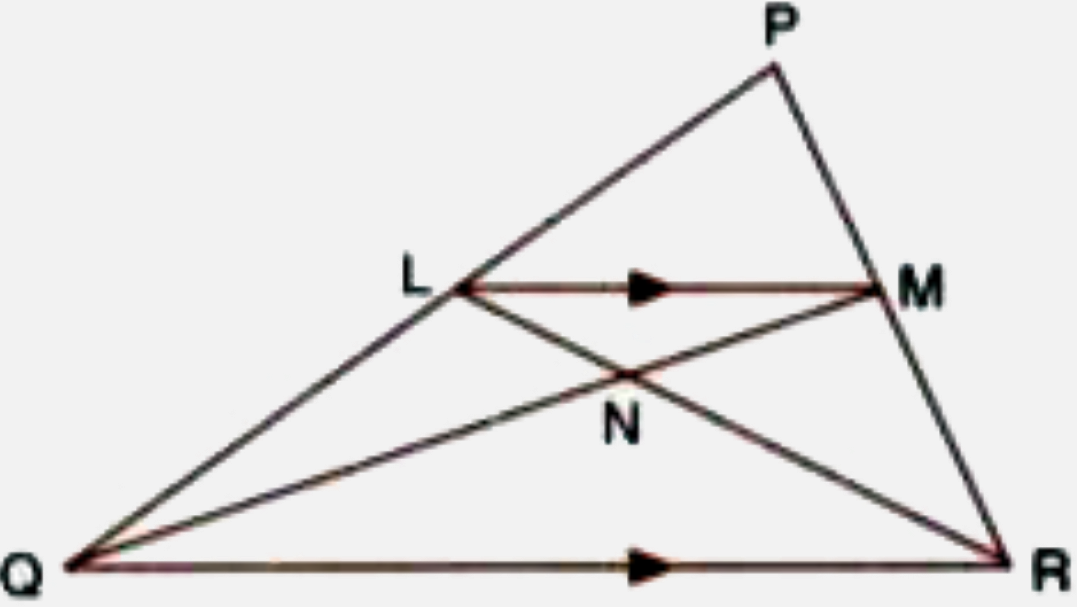
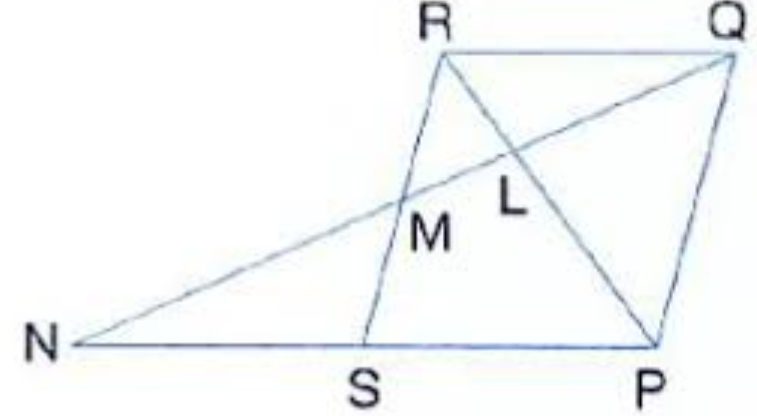
View SolutionIn the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that `RL : LP = 2:3`. QL produced meets RS at M and PS produced at N.
Find the lengths of PN and RM.
View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
`AE : EC = BE : ED`.
Show that : ABCD is a trapezium.
View SolutionIn triangle `ABC, AD` is perpendicular to side BC and `AD^2 = BD xx DC`.
Show that angle `BAC = 90^@`.
View SolutionIn the given figure, `AB////EF////DC, AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm`.
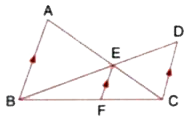
Name the three pairs of similar triangles.
View SolutionIn the given figure, `AB////EF////DC, AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm`.
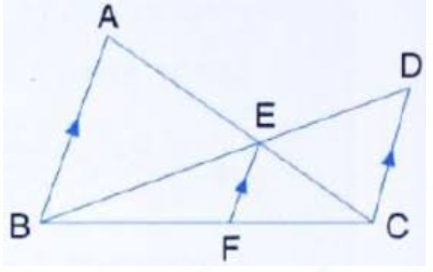
Find the lengths of EC and EF.
View SolutionIn the given figure, QR is parallel to AB and DR is parallel to QB.
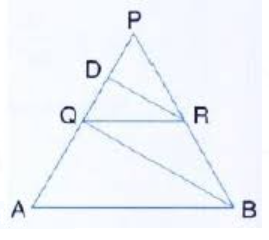
Prove that : `PQ^2 = PD xx PA`.
View SolutionThrough the mid-point `M` of the side `C D` of a parallelogram `A B C D` , the line `B M` is drawn intersecting `A C` at `La n dA D` produced at `E` . Prove that `E L=2B Ldot`
View SolutionIn the given figure, P is a point on AB such that `AP : PB = 4: 3`. PQ is parallel to AC.
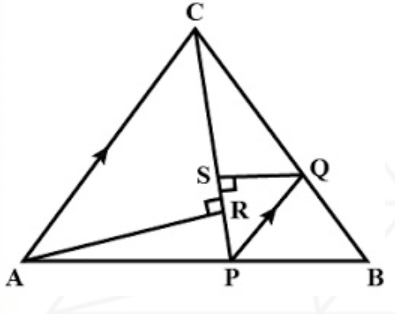
Calculate the ratio PQ : AC, giving reason for your answer.
View SolutionIn the given figure, P is a point on AB such that `AP : PB = 4: 3`. PQ is parallel to AC.
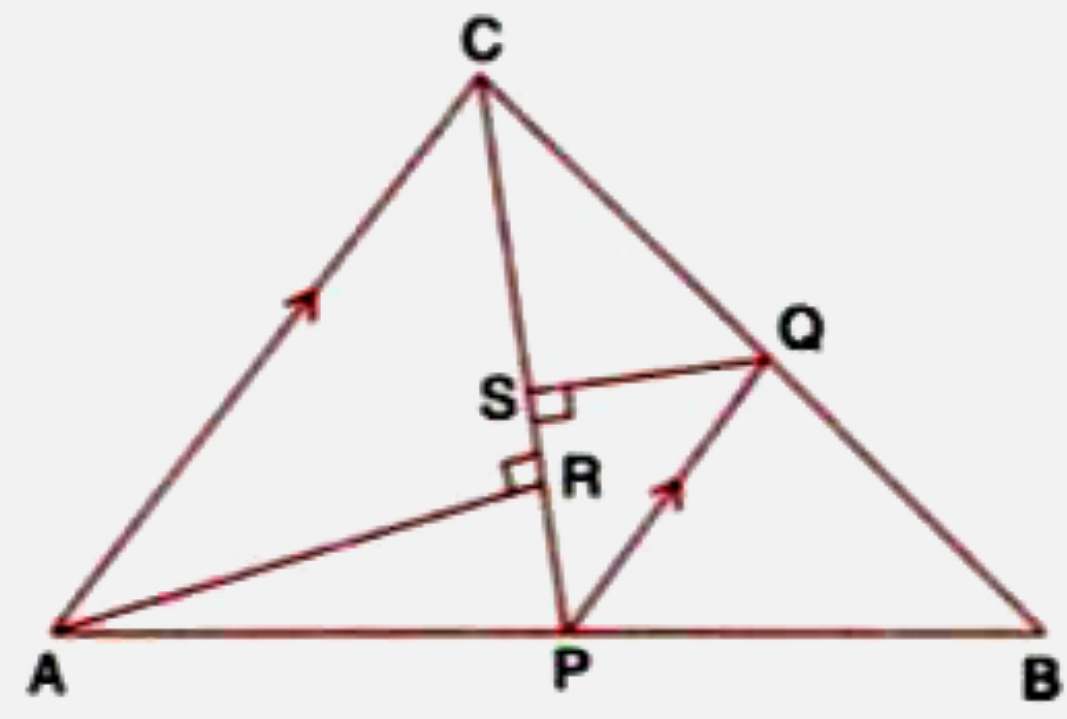
In triangle `ARC, /_ARC = 90^@` and in triangle `PQS,, /_PSQ = 90^@`. Given `QS = 6 cm`, calculate the length of AR.
View SolutionIn the right-angled triangle QPR, PM altitude.
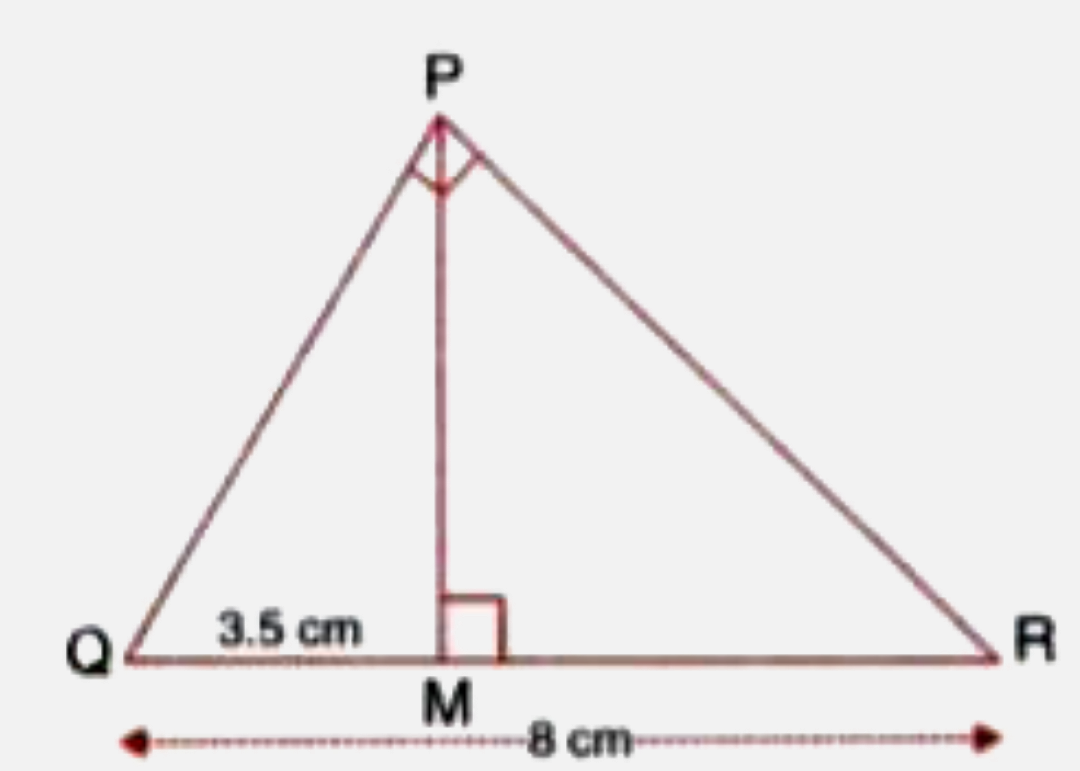
Given that QR = 8 cm and MQ = 3-5 cm, calculate the value of PR.
View SolutionIn the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:
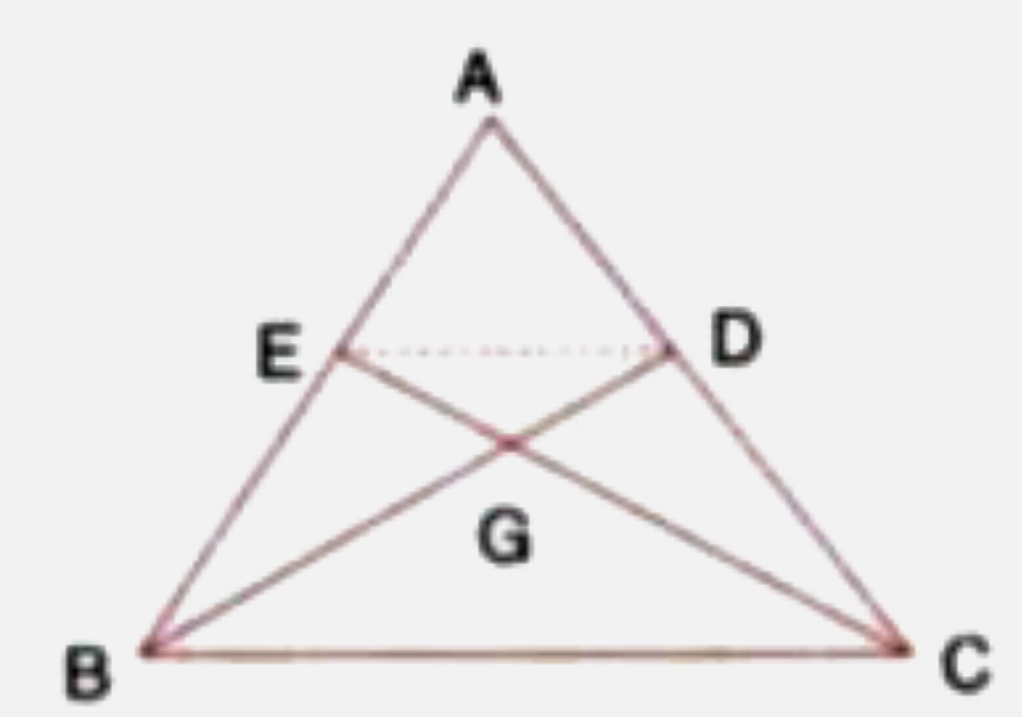
`DeltaEGD - DeltaCGB `and (ii) `BG = 2 GD` from (i) above.
View Solution
EXERCISE 15(A) questions and complete solutions for chapter SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS) of SELINA MATHS (ENGLISH) of Class 10