Complete Solutions to TEXTBOOK CORNER (EXERCISE 2.3) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| OSWAAL PUBLICATION | TEXTBOOK CORNER (EXERCISE 2.3) |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
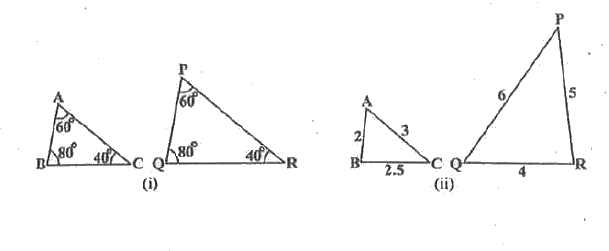
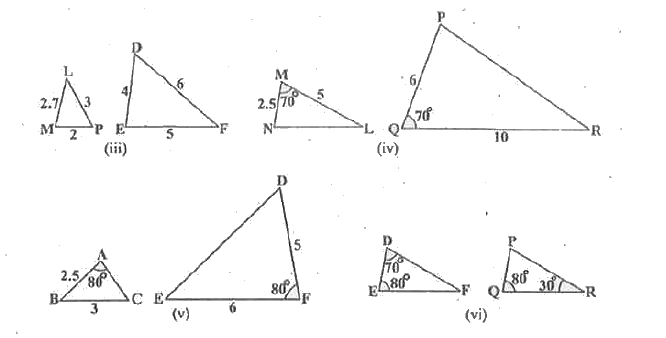
State which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question also write the pairs of similar triangles in the symbolic form:
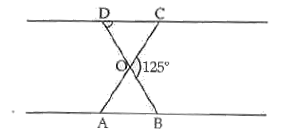
View SolutionIn the figure given below, `Delta ODC - Delta OBA`, `/_ BOC = 125^(@)` and `/_ CDO = 70^(@)`. Find `/_ DOC`, `/_ DCO` and `/_ OAB`
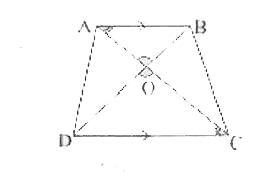
View SolutionDiagonlas AC and BD of a trapezium ABCD with AB ||DC intersect each other at the point O. using a similarity criterion for two triangles, show that `(OA)/(OC) = (OB)/(OD)`.
View SolutionIn Fig . `(QR)/(QS) = (QT)/(PR)and` `|__ul(1)=|__ul(2)` . Show that `Delta PQS ~ Delta TQR`
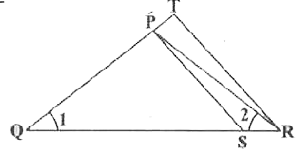
View SolutionS and T are point on sides `PR` and `QR` of `Delta PQR` such that `/_ P = /_ RTS`. Show that `Delta RPQ - Delta RTS`.
View SolutionIn Fig. If `Delta ABE = ACD` , show that `Delta ADE ~ Delta ABC` .
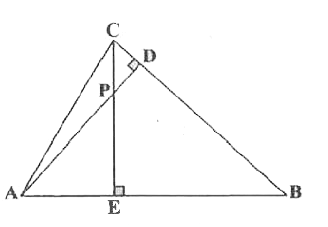
View SolutionIn Fig. Altitudes AD and CE of `Delta ABC ` intersect each other at the point P . Show that :
(i) `DeltaAEP~DeltaCDP`
(ii) `DeltaABD~DeltaCBE`
(iii) `DeltaAEP ~DeltaADB`
(iv) `Delta PDC ~DeltaBEC`
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. show that `DeltaABE ~DeltaCFB`
View SolutionIn Fig , ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
`DeltaABC ~DeltaAMP`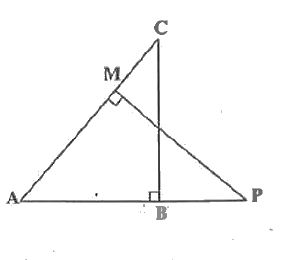
View SolutionGD and GH are respectively the bisectors of `angleACB and angleEGF` such that D and H lie on sides AB and FE of `DeltaABC and and DeltaEFG` respectively. If `DeltaABC~DeltaFEG` , show that:
`(CD)/(GH) =(AC)/(FG)`
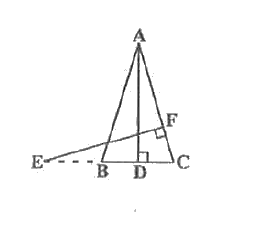
View SolutionIn Fig E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If `ADbotBCandEFbotAC` , prove that `DeltaABD ~DeltaECT`
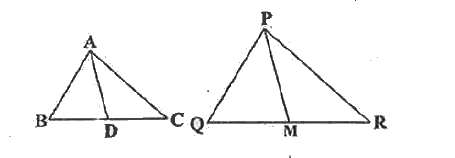
View Solutionsides AB and BC and median AD of a triangle ABC are respectively proportional to side PQ and QR median PM of `DeltaPQR` (see Fig ). Show that `DeltaABC~DeltaPQR`
View SolutionD is a point on the side BC of a triangle ABC such that `angleADC=angleBAC` . Show `CA^(2)=CB.CD`
View Solutionside AB and AC and median AD od a triangle ABC are respectively proportional to side PQ and PR and median PM of another triangle PQR. Show that `DeltaABC~DeltaPQR`
View SolutionA verticle pole of height 6m casts a shadow 4m long on the ground, and at the same time a tower on the same ground casts a shadow 28m long. Find the height of the tower.
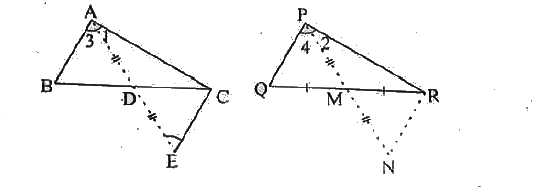
View SolutionIf AD and PM are median of triangles ABC and PQR respectively where `Delta ABC - Delta PQR`, prove that `(AB)/(PQ) = (AD)/(PM)`.
View Solution
TEXTBOOK CORNER (EXERCISE 2.3) questions and complete solutions for chapter TRIANGLES of OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) of Class 10
All Exercises from OSWAAL PUBLICATION Class 10 MATHS TRIANGLES
- TEXTBOOK CORNER (EXERCISE 2.1)
- TEXTBOOK CORNER (EXERCISE 2.2)
- TEXTBOOK CORNER (EXERCISE 2.3)
- TEXTBOOK CORNER (EXERCISE 2.4)
- TEXTBOOK CORNER (EXERCISE 2.5)
- TEXTBOOK CORNER (EXERCISE 2.6)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (MULTIPLE CHOICE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-3 AREA OF SIMILAR TRIANGLES (MULTIPLE CHOICE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-4 PYTHAGOREAN TRIPLETS (MULTIPLE CHOICE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-5 PYTHAGORAS THEOREM (SHORT ANSWER TYPE QUESTIONS)