Complete Solutions to TEXTBOOK CORNER (EXERCISE 2.4) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| OSWAAL PUBLICATION | TEXTBOOK CORNER (EXERCISE 2.4) |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Let `DeltaABC~DeltaDEF` and their areas be , respectively , `64 cm^(2) and 121cm^(2)` . If EF = 15.4 cm, find BC
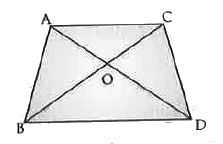
View SolutionDiagonals of a trapezium ABCd with `AB||DC` intersect each other at the point O. If AB = 2 CD , find the ratio of the areas of triangles AOB and COD.
View SolutionIn the figure given below, ABC and DBC are two triangles on the same base BC. If AD intersects BC at `O`, show that `(ar(Delta ABC))/(ar(Delta DBC)) = (AO)/(DO)`.
View SolutionD, E and F are respectively the mid-points of the sides AB, BC and CA of a ΔABC. Prove that by joining these mid-points D, E and F, the ΔABC is divided into four congruent triangles
View SolutionProve that the ratio at the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal of half the area of the equilateral triangle described on one of its diagonals.
View SolutionABC and BDF are two equilateral triangles such that D is the mid -point of BC. Ratio of the areas of triangles ABC and BDF is
View SolutionSides of two similar triangles are in the ratio 4 : 9 Areas of these triangles are in the ratio
View Solution
TEXTBOOK CORNER (EXERCISE 2.4) questions and complete solutions for chapter TRIANGLES of OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) of Class 10
All Exercises from OSWAAL PUBLICATION Class 10 MATHS TRIANGLES
- TEXTBOOK CORNER (EXERCISE 2.1)
- TEXTBOOK CORNER (EXERCISE 2.2)
- TEXTBOOK CORNER (EXERCISE 2.3)
- TEXTBOOK CORNER (EXERCISE 2.4)
- TEXTBOOK CORNER (EXERCISE 2.5)
- TEXTBOOK CORNER (EXERCISE 2.6)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (MULTIPLE CHOICE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-3 AREA OF SIMILAR TRIANGLES (MULTIPLE CHOICE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-4 PYTHAGOREAN TRIPLETS (MULTIPLE CHOICE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-5 PYTHAGORAS THEOREM (SHORT ANSWER TYPE QUESTIONS)