Complete Solutions to TEXTBOOK CORNER (EXERCISE 2.6) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| OSWAAL PUBLICATION | TEXTBOOK CORNER (EXERCISE 2.6) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
In the figure given below, PS is the bisector of `/_ QPR` of `Delta PQR` . Prove that `(QS)/(SR) = (PQ)/(PR)`

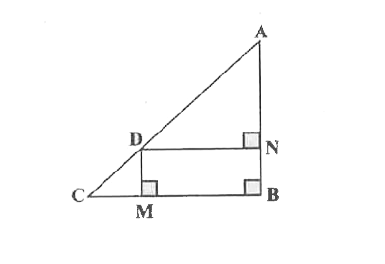
View SolutionIn Fig. D is point on hypotenuse AC of `Delta ABC , BD bot AC DM bot BC and DN bot AB ` . Prove that :
(i) `DM^(2) = DN . MC` , (ii) `DN^(2) = DM . AN`
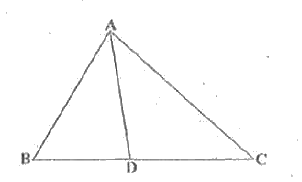
View SolutionIn Fig . ABC is a triangle in which `angleABClt90^(@)and AD botBC.` Prove that `AC^(2)=AB^(2)+BC^(2)-2BC.BD.`
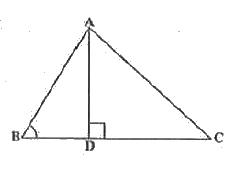
View SolutionIn Fig . ABC is a triangle in which `angleABClt90^(@)and AD botBC.` Prove that `AC^(2)=AB^(2)+BC^(2)-2BC.BD.`

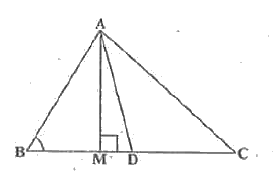
View SolutionIn Fig . AD is a median of a triangle `ABD and AM bot BC.` Prove that :
`AC^(2)+AB^(2)=2AD^(2)+1/2 BC^(2)`
View SolutionProve that the sum of the squares of the diagonals of parallelogram is equal to sum of the squares of its sides.
View SolutionIn Fig . two chords AB and CD intersect each other at the point P. prove that :
`DeltaAPC~DeltaDPB`

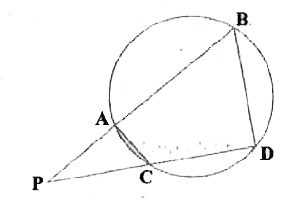
View SolutionIn Fig. two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that (i) `Delta PAC ~ Delta PDB` , (ii) PA . PB = PC . PD
View SolutionIn Fig .D is a point on side BC of`DeltaABC` such that `(BD)/(CD) =(AB)/(AC)` prove that AD is the bisector of `angleBAC.`
View SolutionNazima is fly fishing in a stream. The tip of her fishing rod is `1.8 m` above the surface of water and the fly at the end of the string rests on the water `3.6 m` away and `2.4 m` from a point directly under the tip of the rod. Assuming that her rod to the fly) is taut, how much string does she have out(see fig)? If she pulls in the string at the rate of 5 cm per second, what will be the heriozontal distance of the fly from her after 12 seconds.

View Solution
TEXTBOOK CORNER (EXERCISE 2.6) questions and complete solutions for chapter TRIANGLES of OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) of Class 10
All Exercises from OSWAAL PUBLICATION Class 10 MATHS TRIANGLES
- TEXTBOOK CORNER (EXERCISE 2.1)
- TEXTBOOK CORNER (EXERCISE 2.2)
- TEXTBOOK CORNER (EXERCISE 2.3)
- TEXTBOOK CORNER (EXERCISE 2.4)
- TEXTBOOK CORNER (EXERCISE 2.5)
- TEXTBOOK CORNER (EXERCISE 2.6)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (MULTIPLE CHOICE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-3 AREA OF SIMILAR TRIANGLES (MULTIPLE CHOICE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-4 PYTHAGOREAN TRIPLETS (MULTIPLE CHOICE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-5 PYTHAGORAS THEOREM (SHORT ANSWER TYPE QUESTIONS)