Complete Solutions to TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS) of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| OSWAAL PUBLICATION | TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS) |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
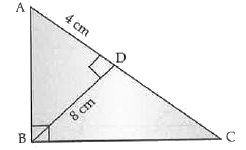
In `Delta ABC`, `/_ ABC = 90^(@)`, `BD _|_ AC`. If `BD = 8 cm`, `AD = 4 cm`, find CD .
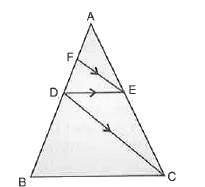
View SolutionIn `Delta ABC`, `DE || BC` and `CD || EF`. Prove that `AD^(2) = AF.AB`.
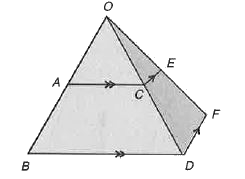
View SolutionIn the following figure, `AC || BD` and `CE || DF`. If `OA = 13 cm`, `AB = 9 cm`, `OC = 8 cm` and `EF = 4.5 cm`, find OE.
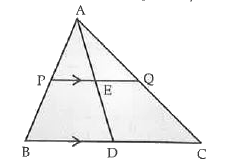
View SolutionIn `Delta ABC`, AD is the median and `PQ || BC`. Prove that `PE = EQ`
View SolutionIn `Delta ABC`, `PQ ||BC`, `AP = 3 cm`, `AR = 4.5 cm`, `AQ = 6 cm`, `AB = 5 cm` and `AC = 10 cm`. Find the length of AD.
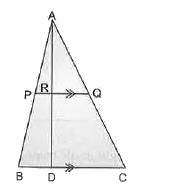
View SolutionIf one diagonal of a trapezium divides the other in the ration `1 : 2`, then prove that one of the parallel sides is twice the other.
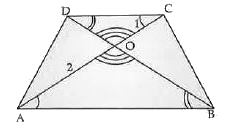
View SolutionA ladder resting against a vertical wall has its foot on the ground at the distance of 6 cm from wall. A man climbs two third of the ladder. What will be his distance from the wall now ?
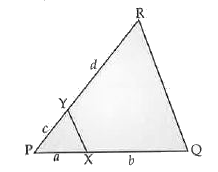
View SolutionStudy the following figure. Write the ratios in relation to basic proportionality theorem and its corollarise, in terms of a, b, c and d.
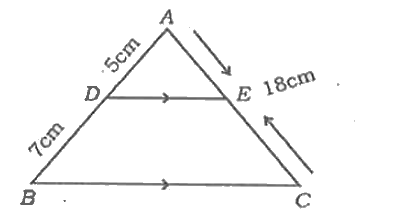
View SolutionIn `Delta` ABC , DE `||` BC . If AD= 5 cm , BD = 7 cm and AC = 18 cm , find the length of AE.
View SolutionIn the given figure, `AC || BD` and `CE || DF`. If `OA = 12 cm`, `AB = 9 cm`, `OC = 8 cm` and `EF = 4.5 cm`, find OE.
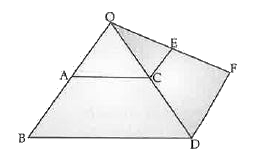
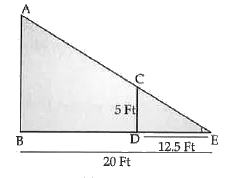
View SolutionAt certain times of the day trees casts its shadow 12.5 feet long. If the height of the tree is 5 feet, find the height of another tree the casts its shadow 20 feet long at the same times.
View SolutionX is any point inside `Delta ABC`, XA, XB and XC are joined 'E' is any point on AX. If `EF || AB`,`FG || BC`. Peove that `EG || AC`.

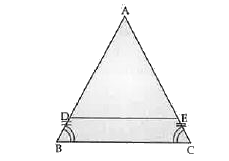
View SolutionIn `Delta ABC`, `/_ B = /_C`, D and E are the points on AB and AC such that `BD = CE`, prove that `DE || BC`.
View Solution`Delta ABC - Delta DEF`, Area of `Delta ABC = 64 cm^(2)` and area of `Delta DEF = 121 cm^(2)`. If `EF = 15.4 cm`, Find BC.
View SolutionIn `Delta ABC`, `/_ ABC = 90^(@)`, `BM _|_ AC`, `AM = 8x^(2)`,`AM = 2x^(2)`, find BM and AB.

View SolutionFrom the following data, State whether `Delta ABC` is similar to `Delta DEF` or not :
(a) `/_ A = 70^(@)`, `/_B = 80^(@)`, `/_ D = 70^(@)`, `/_ F= 30^(@)`
(b) `AB = 8 cm`, `BC = 9 cm`, `CA = 15 cm`, `DE = 4 cm`, `EF = 3 cm`, `FD = 5 cm`.
View SolutionSelect the set of numbers in the following, which can form similar triangles.
(I) 3, 4, 6 (II) 9, 12, 18
(III) 8, 6, 12 (IV) 3, 4, 9
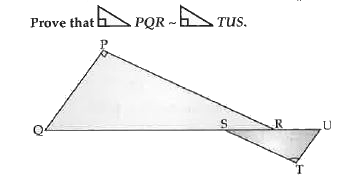
View SolutionIn the figure, `/_ QPR = /_ UTS = 90^(@)` and `PR || TS`. Prove that
View SolutionIn the following figure, `/_ ABC = 90^(@)` and `/_ AMP = 90^(@)`. Prove that : (I)
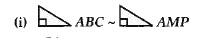
(II) `(CA)/(PA) = (BC)/(MP)`
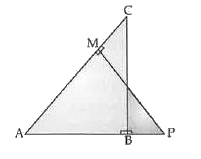
View Solution
TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS) questions and complete solutions for chapter TRIANGLES of OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) of Class 10
All Exercises from OSWAAL PUBLICATION Class 10 MATHS TRIANGLES
- TEXTBOOK CORNER (EXERCISE 2.1)
- TEXTBOOK CORNER (EXERCISE 2.2)
- TEXTBOOK CORNER (EXERCISE 2.3)
- TEXTBOOK CORNER (EXERCISE 2.4)
- TEXTBOOK CORNER (EXERCISE 2.5)
- TEXTBOOK CORNER (EXERCISE 2.6)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (MULTIPLE CHOICE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-1 BASIC PROPORTIONALITY THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-3 AREA OF SIMILAR TRIANGLES (MULTIPLE CHOICE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-3 AREA OF SIMILAR TRIANGLES (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-4 PYTHAGOREAN TRIPLETS (MULTIPLE CHOICE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (SHORT ANSWER TYPE QUESTIONS)
- TOPIC-4 PYTHAGOREAN TRIPLETS (VERY SHORT ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS)
- TOPIC-5 PYTHAGORAS THEOREM (LONG ANSWER TYPE QUESTIONS-(II))
- TOPIC-5 PYTHAGORAS THEOREM (SHORT ANSWER TYPE QUESTIONS)