The diagonal BD of parallelogram ABCD intersect AE at F as shown in the figure. If E is any point on BC, then prove that DF×EF=FB=FA.Solution in Kannada
Step by step video & image solution for The diagonal BD of parallelogram ABCD intersect AE at F as shown in the figure. If E is any point on BC, then prove that DFxxEF=FB=FA. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - ZEE ADDITIONAL QUESTIONS - SHORT ANSWER TYPE - 2 QUESTIONS
7 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
10 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - ZEE ADDITIONAL QUESTIONS - VERY SHORT ANSWER QUESTIONS
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS -HOTS [HIGHER ORDER THINKING SKILLS]-QUESTIONS
11 Videos
Similar Questions
Prove that if the area of similar triangles are equal, they are congruent.
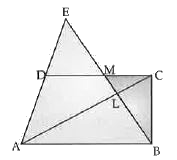
View SolutionThrought the mid-point M of the sides of a parallelogram ABCD, the line BM is drawn intersecting AC at L, and AD produced to E. Prove that EL=2BL.
View SolutionIn ΔABC, D and E are points on AB and AC respectively, such that DE∣∣BC. If ADDB=413 and AC = 20.4 cm, find AE.
View SolutionA sector of a circular is of radius 12 cm and angle 120∘. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DFxEF=FBxFA.
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the Side BC. Prove that DF×EF=FB×FA.
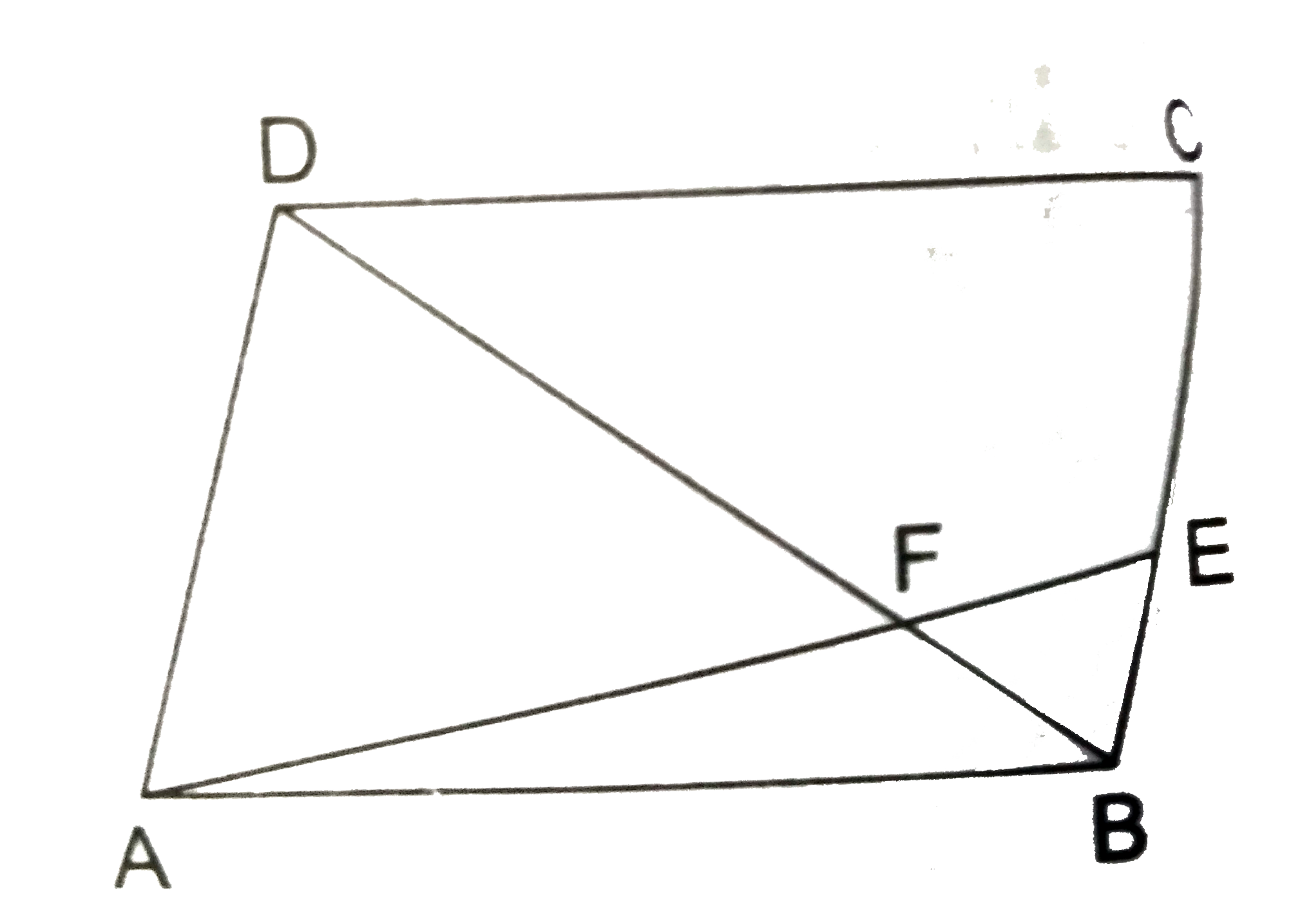
View SolutionABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
View Solutionकिसी समान्तर चतुर्भुज ABCD का विकर्ण BD , रेखा AE को बिन्दु F पर प्रतिच्छेदित करता है , जहाँ बिन्दु E , भुजा BC पर स्थित है , तो सिद्ध कीजिए कि DF×EF=FB×FA.
View Solutionबगल के चित्र में समान्तर चतुर्भुज ABCD का विकर्ण BD रेखा खण्ड AE को F बिन्दु पर प्रतिच्छेद करता है , जहाँ E,BC भुजा पर कोई बिन्दु है । दिखाएँ कि DF×FE=BF×FA.
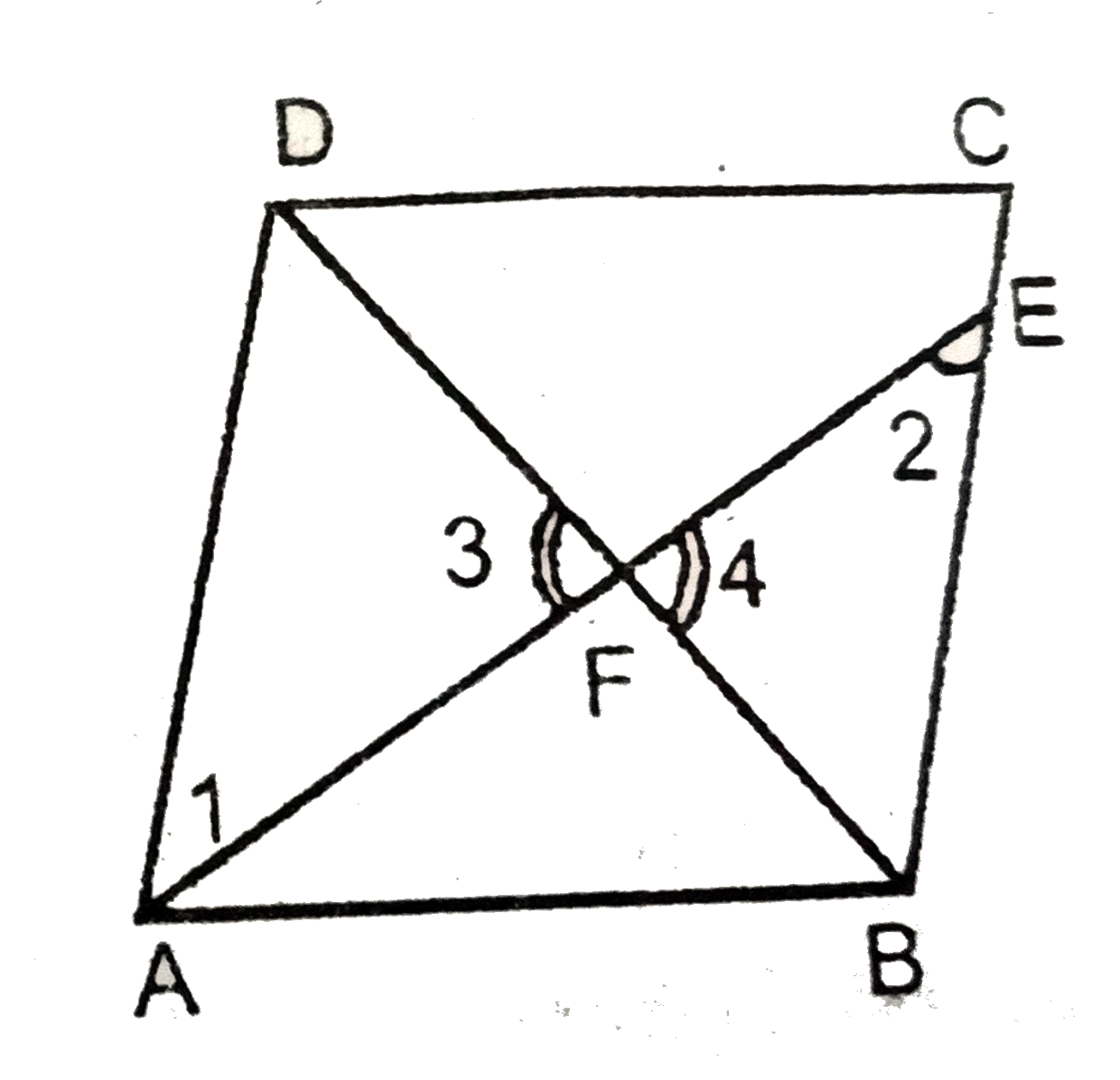
View Solutionएक समानांतर चतुर्भुज ABCD की भुजा BC , पर एक बिंदु E स्थित है|यदि इस समानांतर चतुर्भुज का विकर्ण BD रेखा AE को बिंदु F पर काटता हों,तो सिद्ध करो की: DF×EF×=FB×FA
View SolutionThe diagonal BD of parallelogram ABCD intersect AE at F as shown in the figure. If E is any point on BC, then prove that DF×EF=FB=FA.
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ΔAPD=ΔCPD.
View SolutionABCD एक समांतर चतुर्भुज है जिसके विकर्ण E बिंदु प्रतिच्छेद करते है। AC को F तक इस तरह बढाया गया हैं कि CF = AE सिध्द कीजिए। कि ar (ΔBDF)=ar(∣∣gmABCD)
View SolutionABCD is a parallelogram as shown in the figure. 'E' is a point on BC, the diagonal BD intersects AE in 'F'. Then prove that DF x EF = FB x FA.
View Solutionएक समान्तर चतुर्भुज ABCD में, विकर्ण BD,रेखाखण्ड AE को बिंदु F पर प्रतिच्छेद करता है। जहाँ भुजा BC पर कोई बिंदु E है, तो सिद्ध कीजिए कि DF×FE=BF×FA
View SolutionE is any point on the side BC of the parallelogram ABCD. AE intersects the diagonal BD at point F. Prove that DF×EF=FB×FA.
View Solution
