Complete Solutions to Example of chapter FORCE ANALYSIS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FORCE ANALYSIS |
| ANURAG MISHRA | Example |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
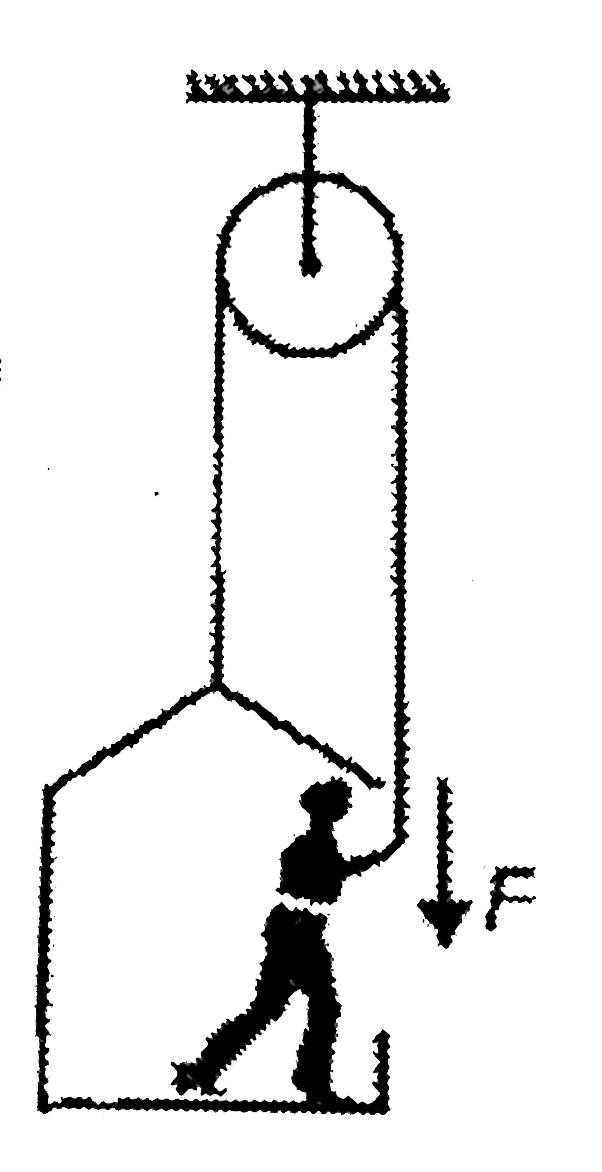
A man of mass M stands on a.box of mass m as shown in the Fig. 2E. l (a). A rope attached to 'the box and passing over an overhead pulley allows the man to raise himself and the box by , pulling the rope downward.
(i) With what minimum force should the ' man pull the rope so as to prevent himself , from falling down.
(ii) If the man pulls the rope with a force F greater than the minimum force, then determine the acceleration of the (man + box) system.
(iii) Determine. the normal reaction between the man and the trolley.
View SolutionA heavy block of mass M hangs in equilibrium at the end of a rope of mass m and length `l` connected to a celling. Determine the tension in the rope at a distance `x` from the ceiling.
View SolutionA bucket is suspended by two light ropes a and b as shown in fig. 2E.3 (a). Determine the tensions in the ropes a and b.

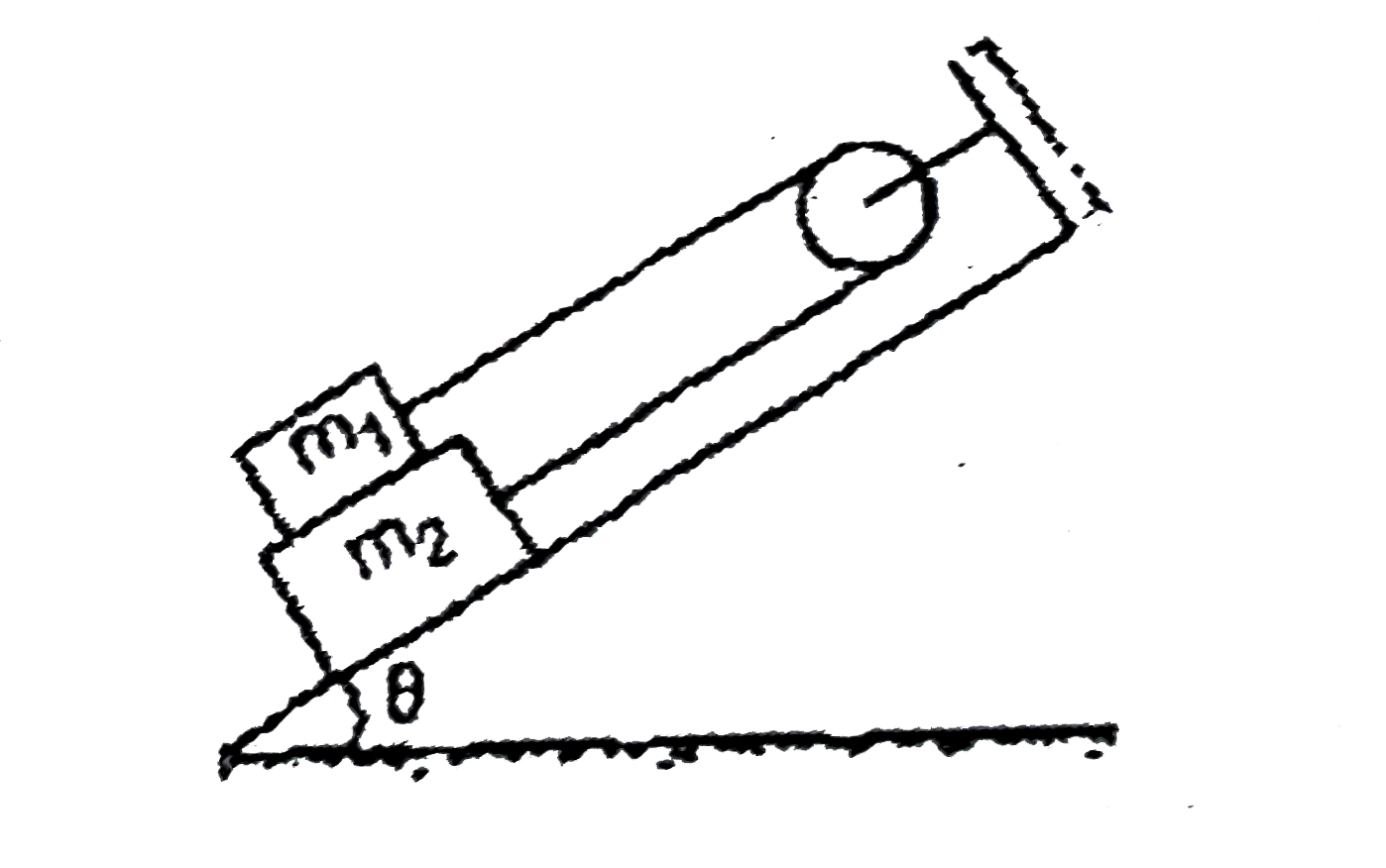
View Solution(a) shows a block of mass `m_(1)` sliding on a block of mass `m_(2)`, with `m_(1) gt m_(2)`. Find
(a) the acceleration of each block,
(b) tension in the string,
(c) force exerted by `m_(1)` on `m_(2)`
(d) force exerted by `m_(2)` on the incline
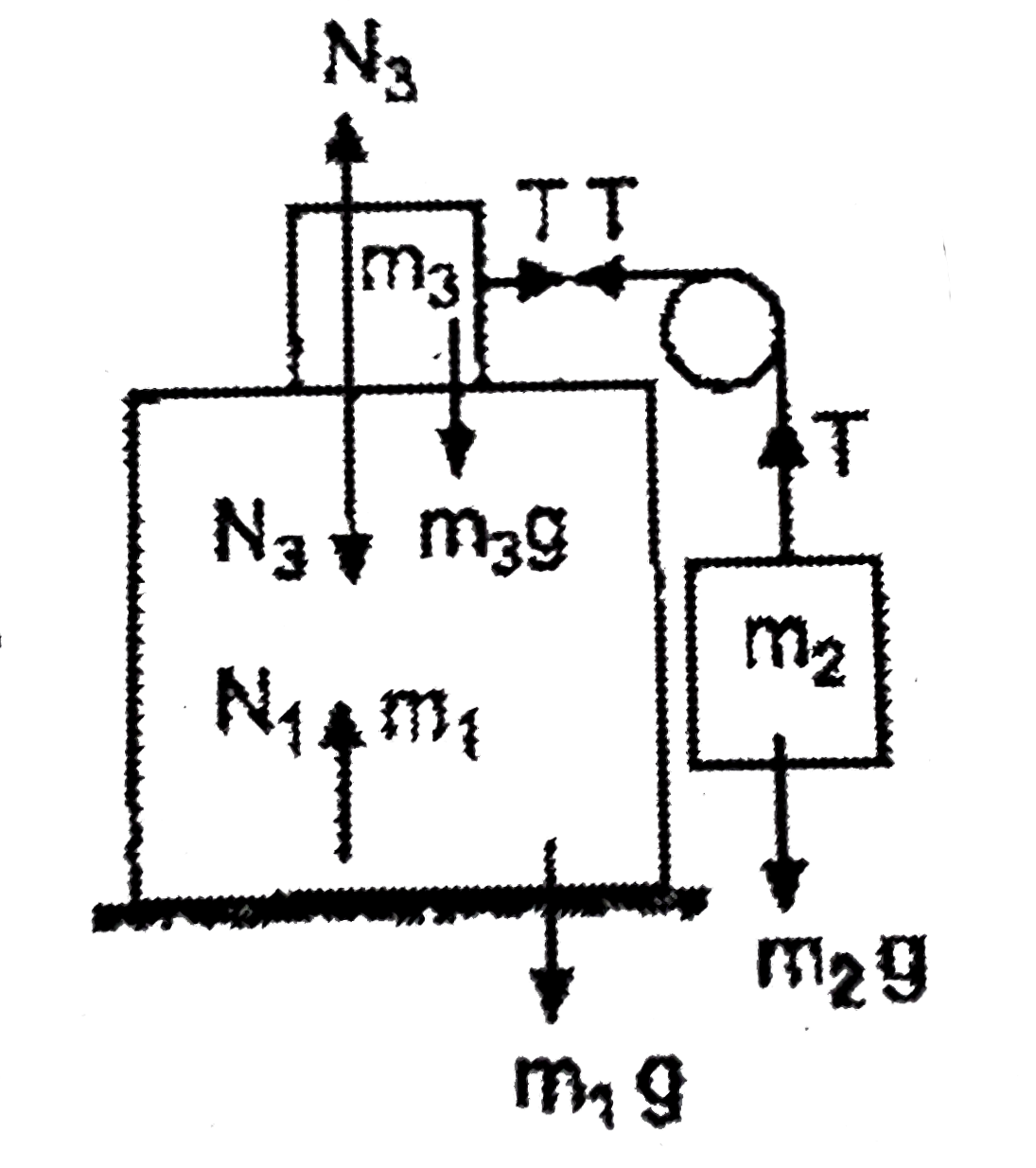
View SolutionIn the system shownin Fig. 2E.5 (a), block `m_(2)` is being prevented from descending by pulling `m_(1)` to the right with force F. Assuming all the surfaces to be surfaces to be frictionless, find F.
View SolutionA block of mass `m_(1)` on a smooth, horizontal· swface is: connected to a second mass `m_(2)` by a light cord ovbr a light,: frictionless pulley as shown. (Neglect the mass of the cord and' of the pulley). A force of magnitude `F_(0)` is applied to mass `m_(1)`· as shown. Neglect any friction.
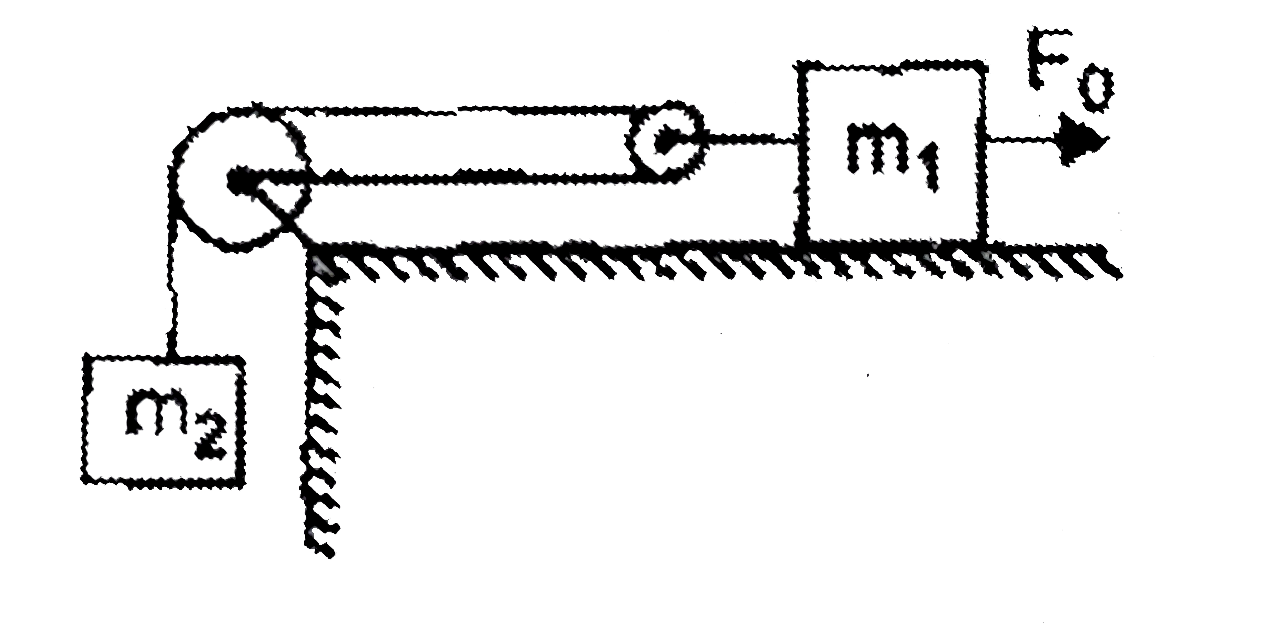
(a) Find the value of force `F_(0)` for which the sy!tem will be in equilibrium.
(b) Find the acceleration of masses andtensio~ in string if `F_(0)` has a value which is double of that foun,d in part (a).
View SolutionA small cubical block is placed on a triangular block M so that ,they touch each other along a smooth inclined contact plane as shown. The, inclined surface makes an angle `theta` With the horizontal. A hqrizontal force F is to be applied on the block mi so that the two bodies move without slipping against each other. Assuming the floor to be smooth also, determine the

(a) normal force with which m and M press against each other and
(b) the magnitude of external force F. Express your answer in terms of m, M, `theta` and `g`.
View SolutionA block of mass 1 kg is kept on the tilted floor ofa lift moving, down with `3 m// s^(2)`. If the block is released from rest as shown, what will be the time taken by block to reach the bottom. What is the normal reaction on the block during the motion?

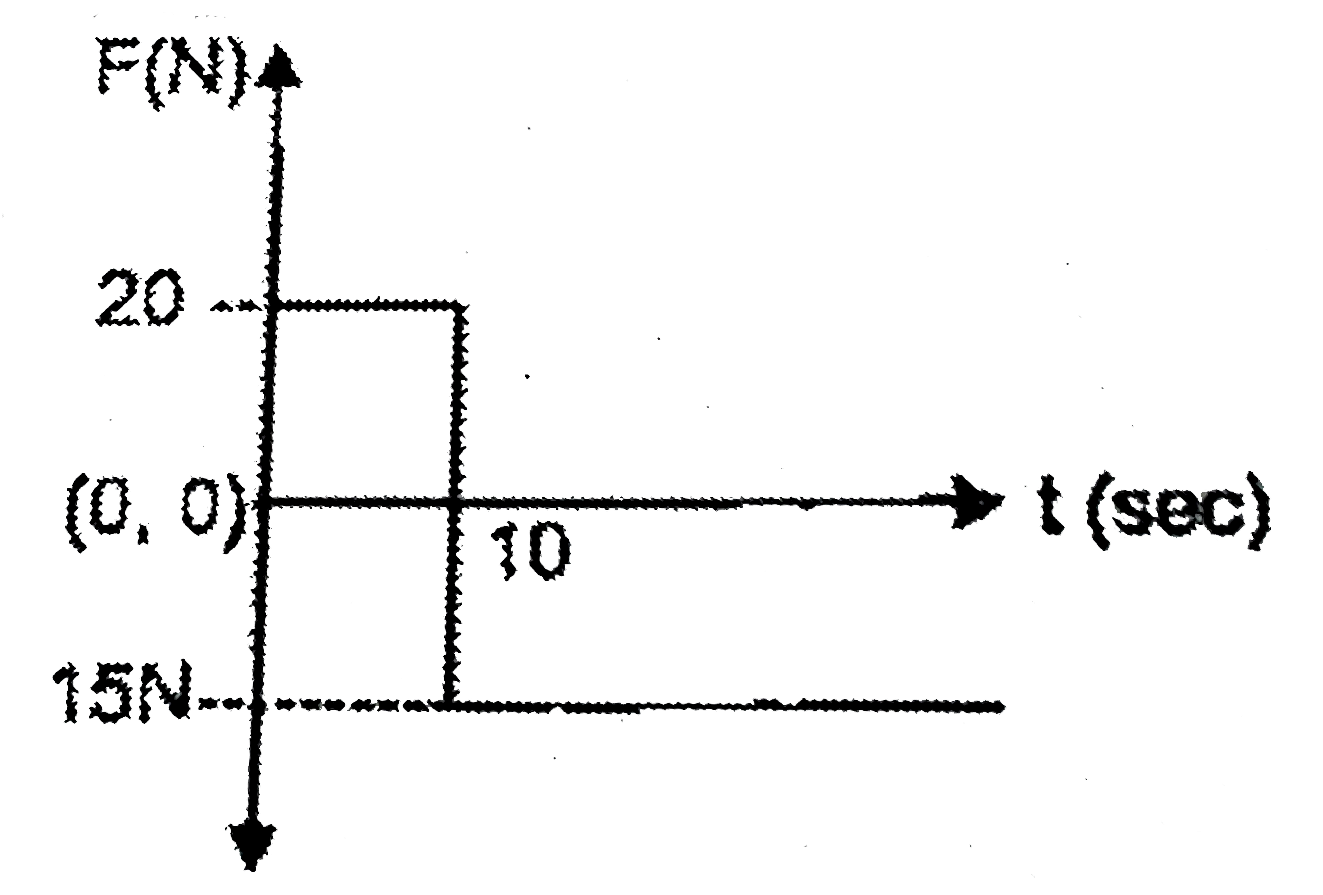
View SolutionA particle of mass 10 kg is acted upon by a force F along the line of motion which varies as shown in the figure. The initial velocity of the particle is `10 ms^(-1)`. Find the maximµm velocity attained by the particle before it comes to instantaneous rest.
View SolutionA homogeneous and flexible chain rests on a wedge whose side edges make-angle `alpha` and `beta` with the horizontal [refer Fig. 2E., 10(a)]. The cehtrarparcuf the chain lies on the upper tip of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the, displacement of the chain with respect to the wedge?
[Consider all surfaces to be smooth]

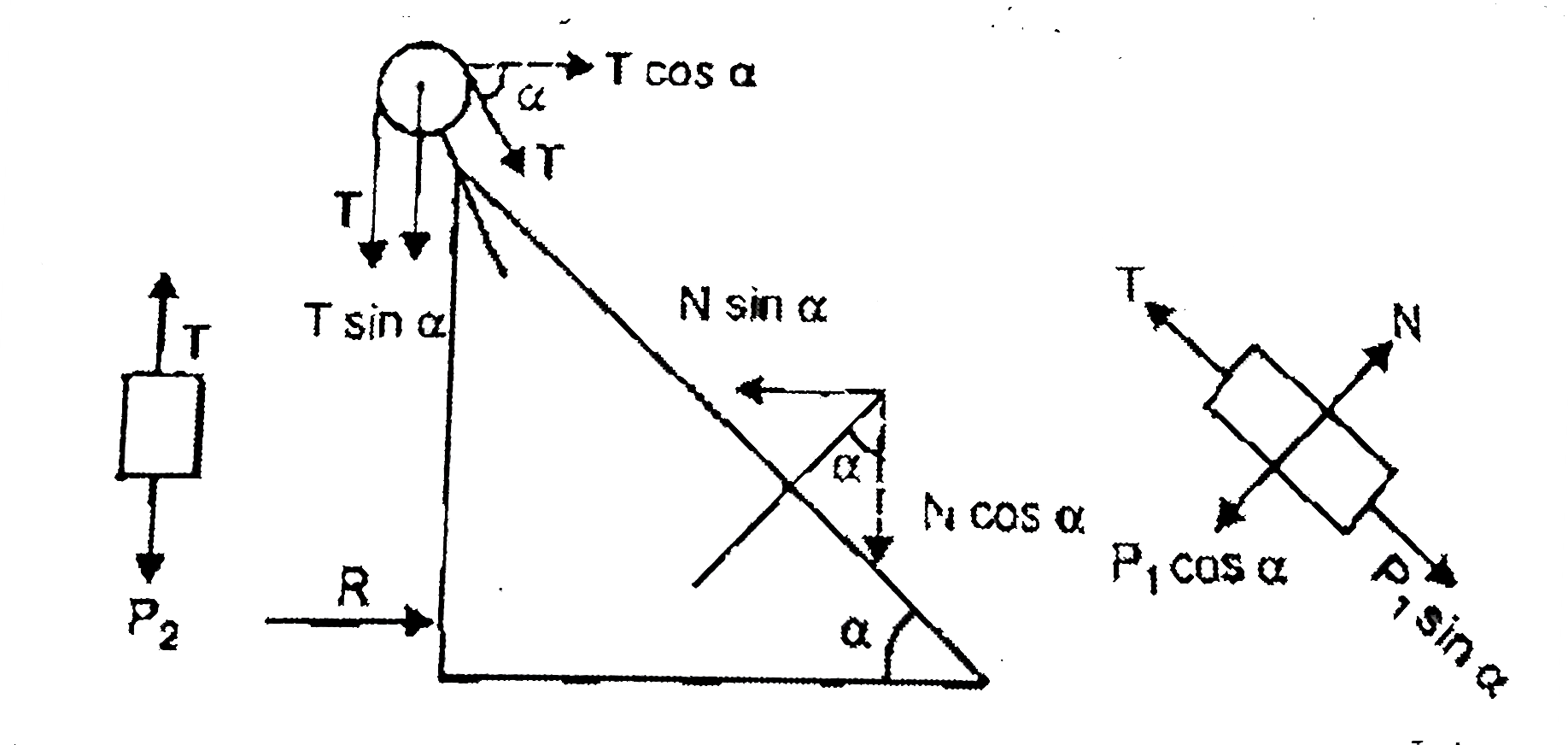
View SolutionA body A weighting `P_(1)` descends down inclined plane D fixed of a wedge which makes an angle `alpha` with the horizontal, and pulls a load B that weights `P_(2)` by means of a weightless and inextensible thread passing over a fixed smooth pulley C, as shown in fig. 2E.11. Determine the horizontal compouent of the force (in Newton) which the wedge acts on the floor corner E.
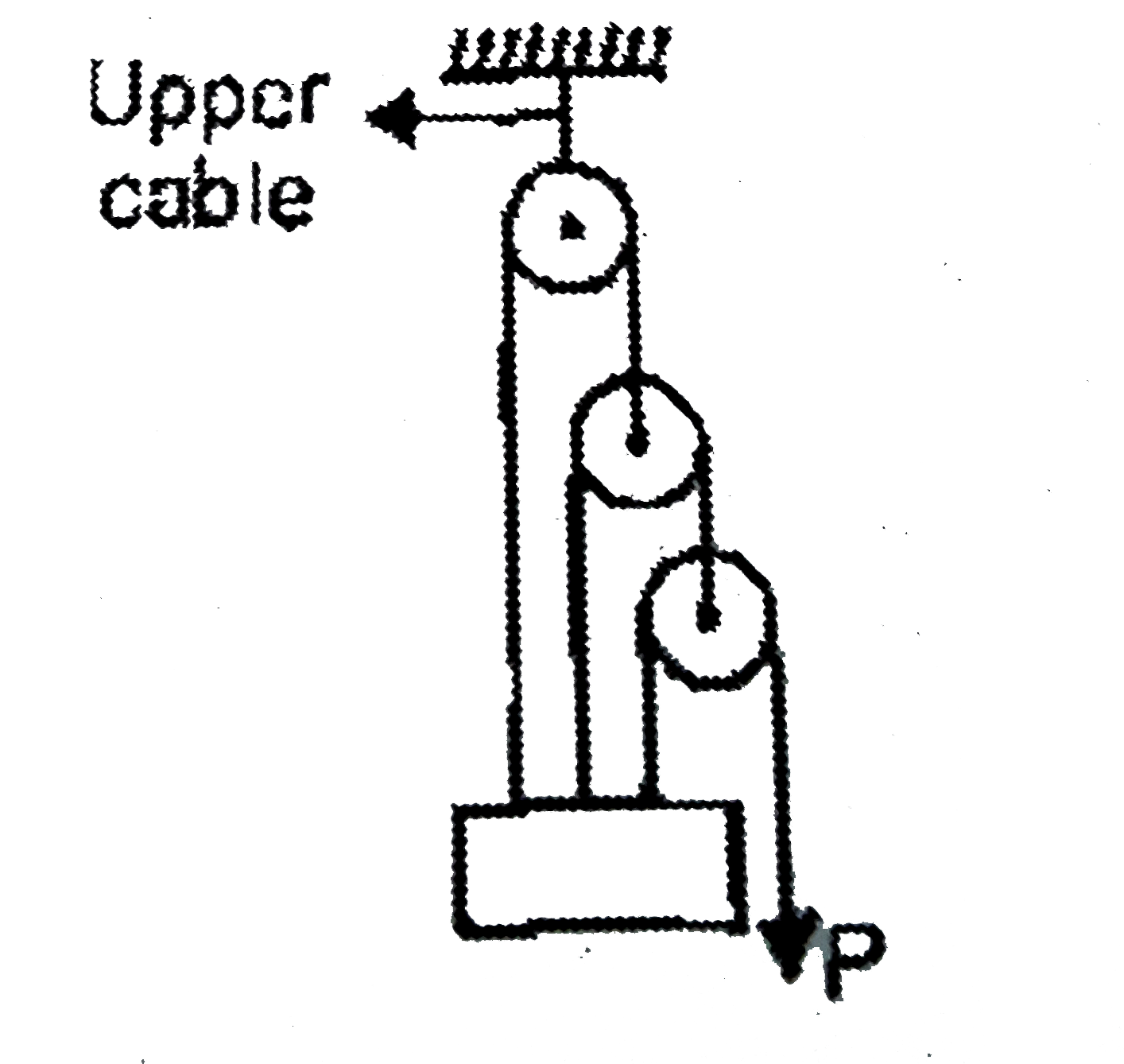
View SolutionThe pull P is is just sufficient to keep the 14 N block in equilibrium as shown. Pulleys are ideal. Find the tension (in N) in the cable connected with ceiling.
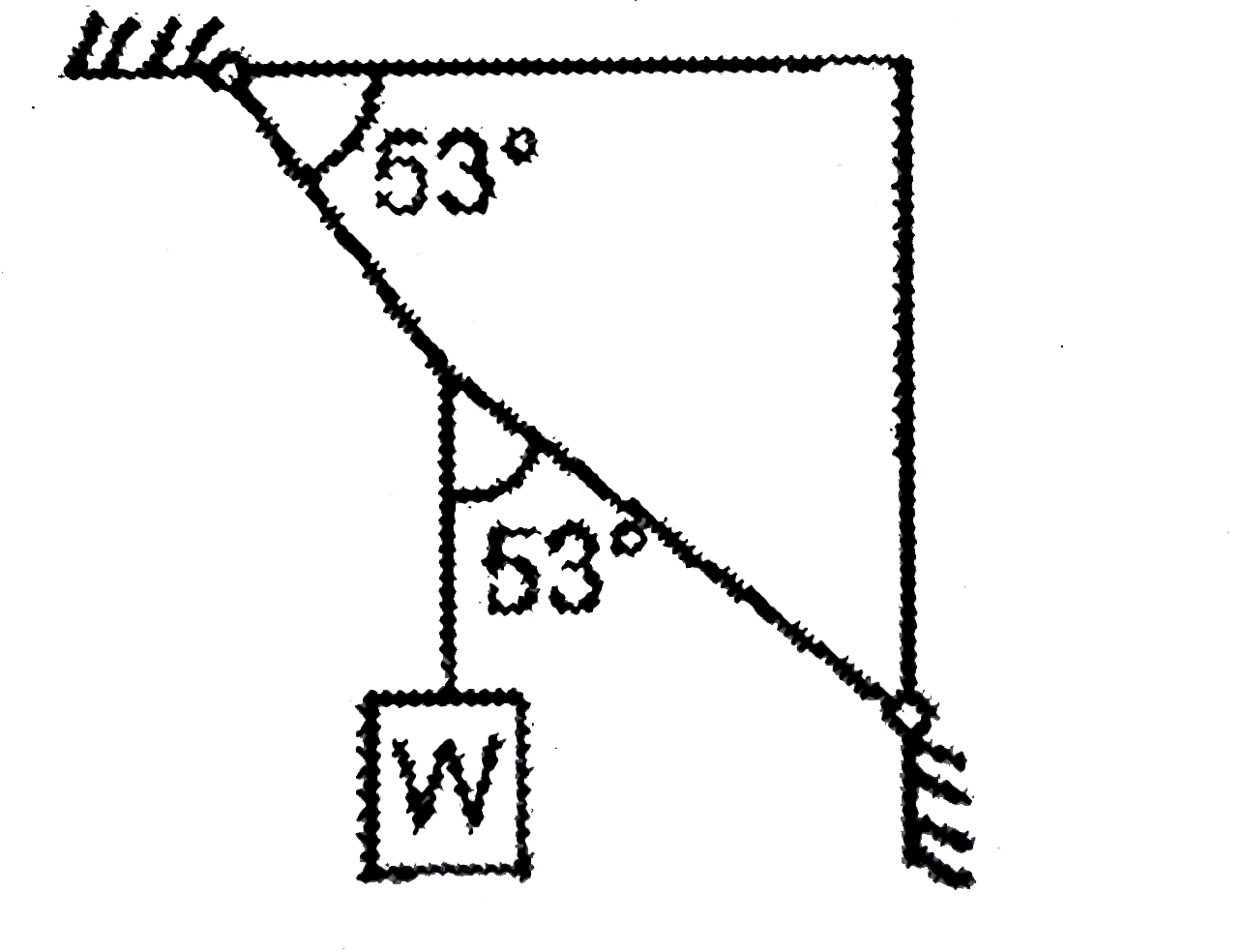
View SolutionFor the equilibrium situation shown, the cords are strong enough to with stand a maximum tension 100 N. what is the largest value of W (in N) that they can support as shown ?
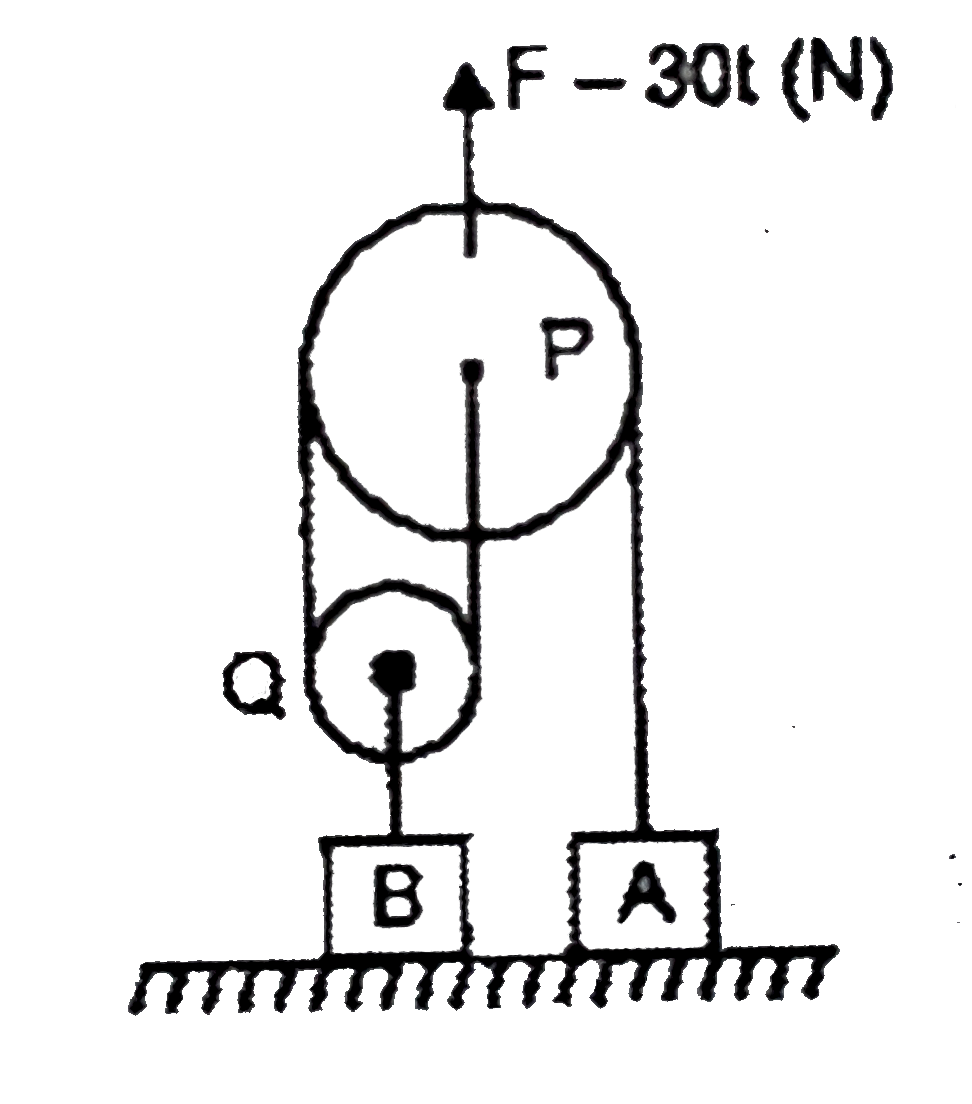
View SolutionTwo block a and B having masses `m_(1)=1 kg, m_(2)=4 kg` are arranged as shown in the figure. The pulleys P and Q are light, and frictionless. All the blocks are resting on. a horizontal floor and the pulleys ate held such that strings remains just taut.
At.moment `t=0 a` force `F=30t (N)` starts acting on thei ipulley p along . vertically upward direction as shown in the pulley P along vertically upward direction as shown in the figure. Calculate.
(i) the time when the blocks A and B loose contact with ground.
(ii) the. velocity of A when B looses contact with ground.
(iii) the height raised. by A upto this instant.
(iv) the work done by the force F upto this instan.
View SolutionIn the figure find the velocity and acceleration of B, if instaneous velocity and acceleration of A are as shown in the Fig.

View SolutionIn the figure shown, friction force between the bend and the light string is `(mg)/4`. Find the time in which the bead loose contact with the string after the system is released from rest.
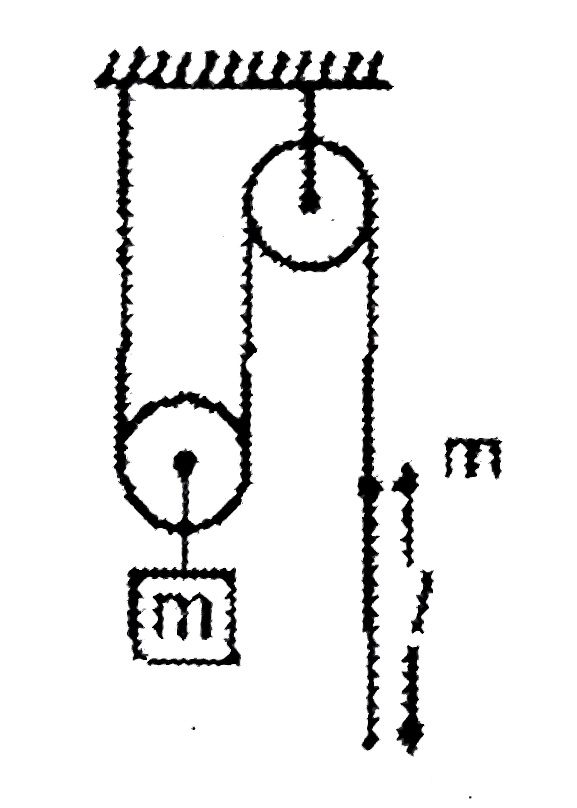
View SolutionIn Fig. shown, both blocks are released from rest. Length of 4 kg block is 2 m and of 1 kg is 4 m. Find the time they take to cross each other? Assume pulley to be light and string to be light and inelastic.
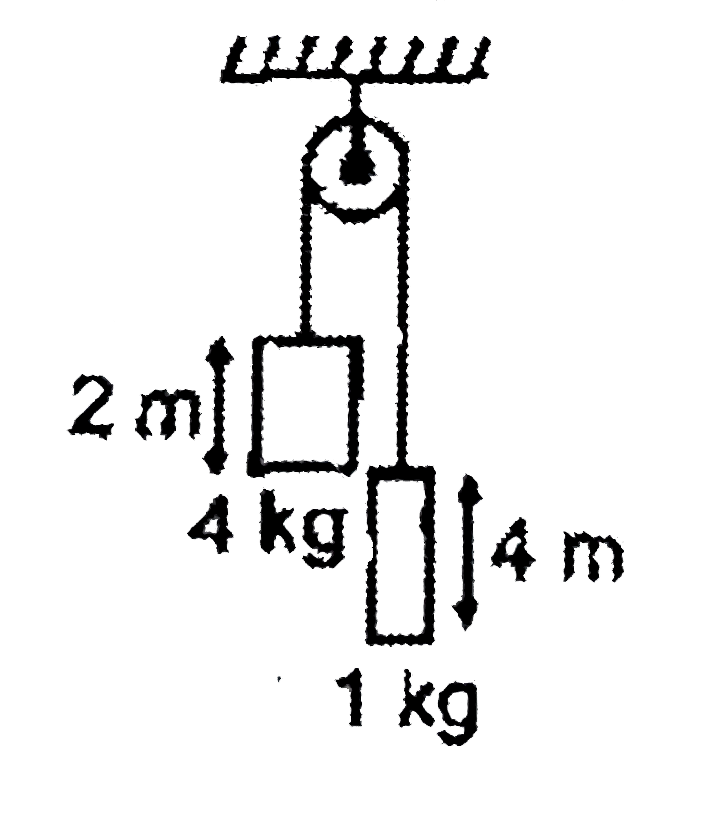
View SolutionA bead C can move freely on a horizontal rod. The bead is connected by blocks B and D by a string as shown in the figure. IF the velocity of B is v. find the velocity of block D.
View SolutionA lift goes up with 10 m/s. a pulley P is fixed to the ceiling of the lift. To this pulley other two pulley `P_(1)` and `P_(2)` are attached. `P_(1)` moves up with velocity 30 m/s. A moves up with velocity 10 m/s. D is moving downwards with velocity 10 m/s at same instant of time. Find the velocity of B and that of C at that instant. Assume that all velocities are relative to the ground.

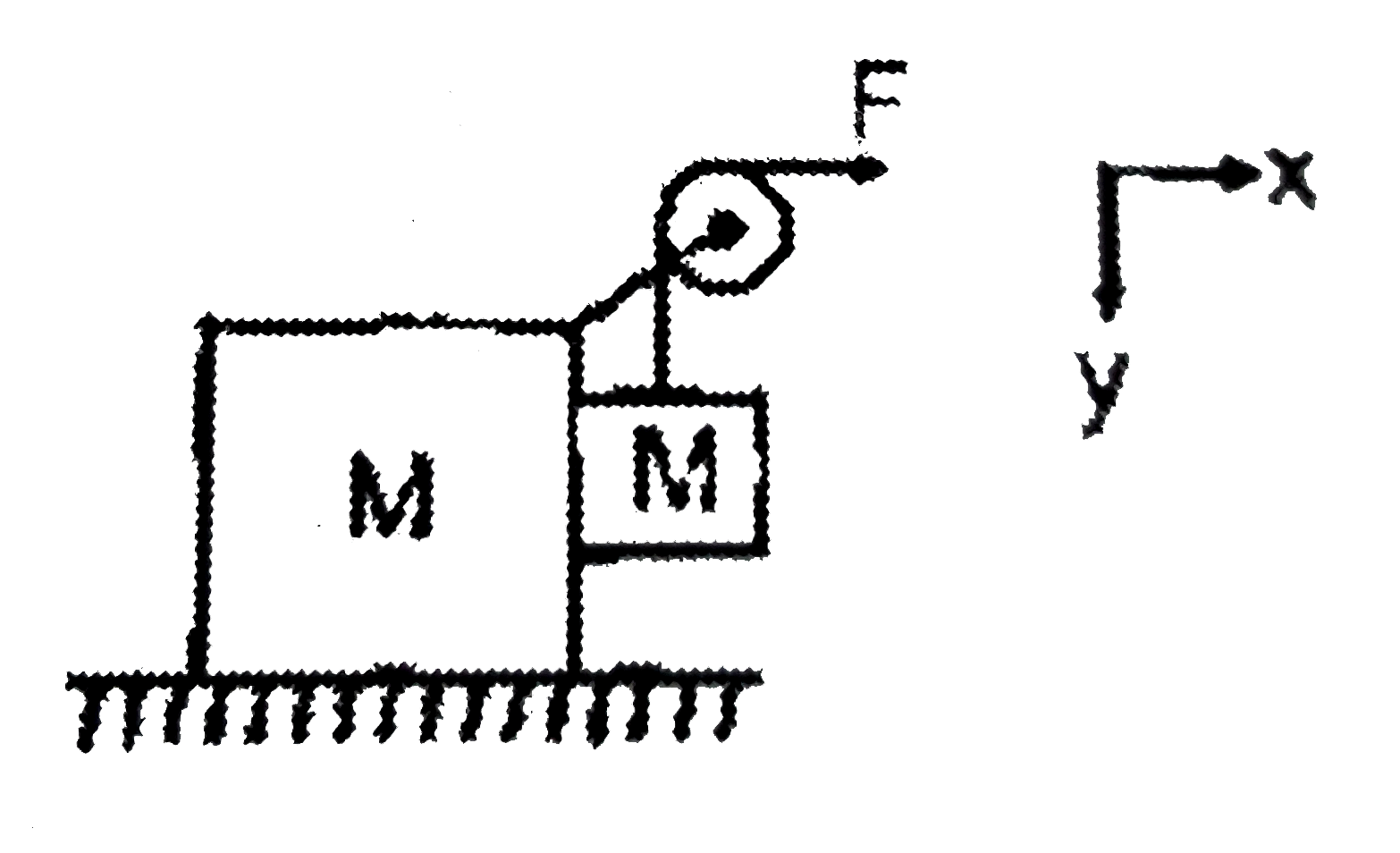
View SolutionIn the situation given all surfaces are frictionless, pulley is ideal and string is light. If `F=Mg//2`, find the acceleration of both the block in vector form.
View SolutionThree blocks shown in move vertically with constant velocities The relative velocity of w.r.t `C` is `100m//s` upward and the relative velocity of `B` w.r.t A is `50m//s` downward. All the string are ideal The velocity of `C` with respect to ground is `125//x` calculate x
 .
.
View SolutionSystem is shown in figure. All the surface are smooth. Rod is move by external agent with acceleration `9 m//s^(2)` vertically downwards. Find the force exerted on the rod by the wedge.

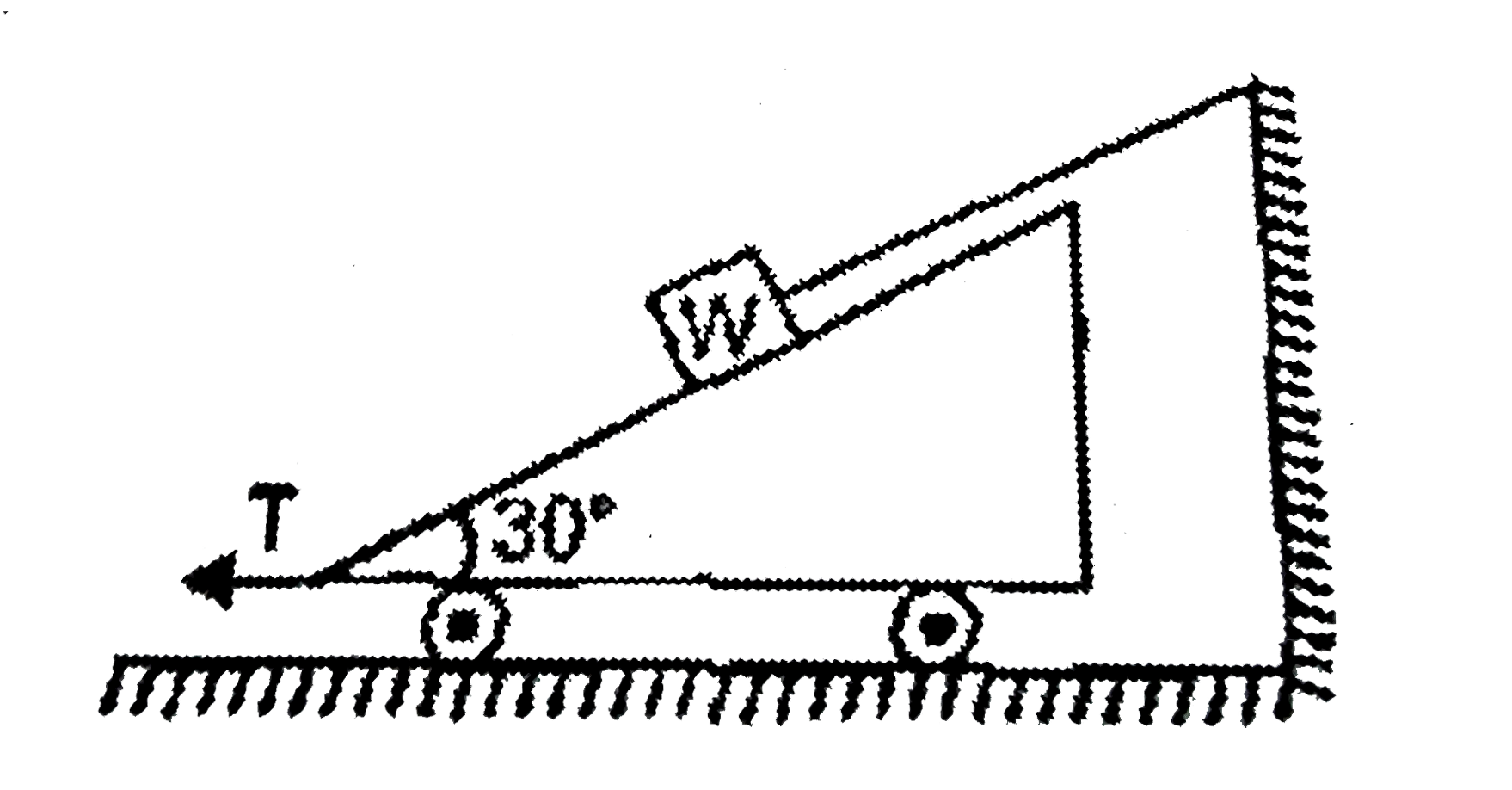
View SolutionFind the tension to hold the car equilibrium, if there is no friction.
View SolutionA steel ball is suspended from the ceiling of an accelerating carriage by means of cords A and B. Determine the acceleration a of the carriage which cause the tension in A to be twice that in B.
View SolutionA block of mass 10 kg is kept on ground. A vertically upward force `F=(20 t)N`, where `t` is the time in seconds starts on it at `t=0`.
(a) Find the time at which the normal reaction acting on the block is zero.
(b) The height of the block from ground at `t=10` sec.
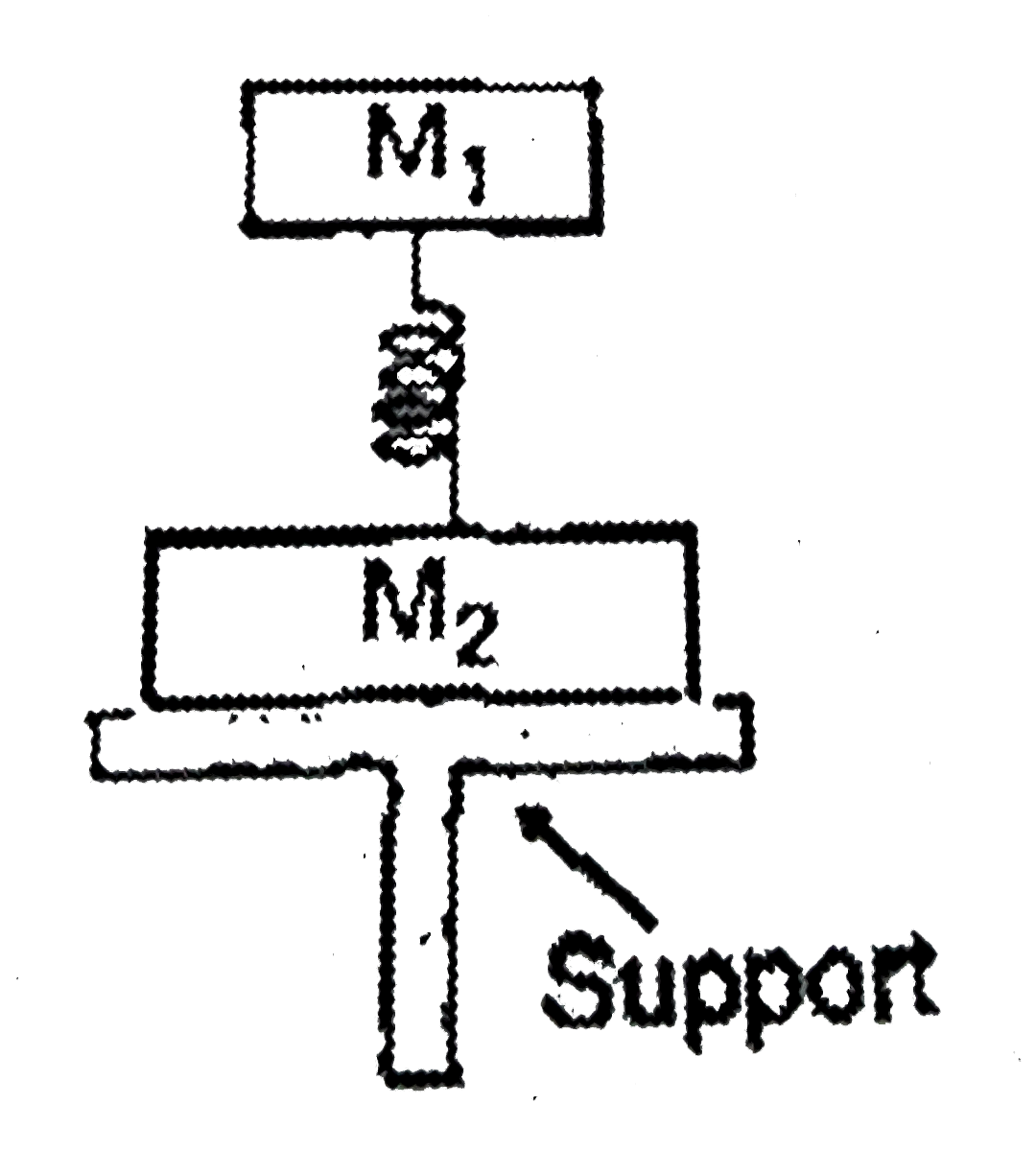
View SolutionThe system of two weights with masses `m_(1)` and `m_(2)` are connected with weightless spring as shown. The system is resting on the support S. the support S is quickly removed. Find the accelerations of each of the weights right after the support S is removed.
View SolutionAn object of mass m is suspended in equilibrium using a string of length `l` and `a` spring of constant `K(lt 2 mg//l)` and unstretched length `1//2`. Find the tension in the string. What happens if `K gt 2 mg//l`?
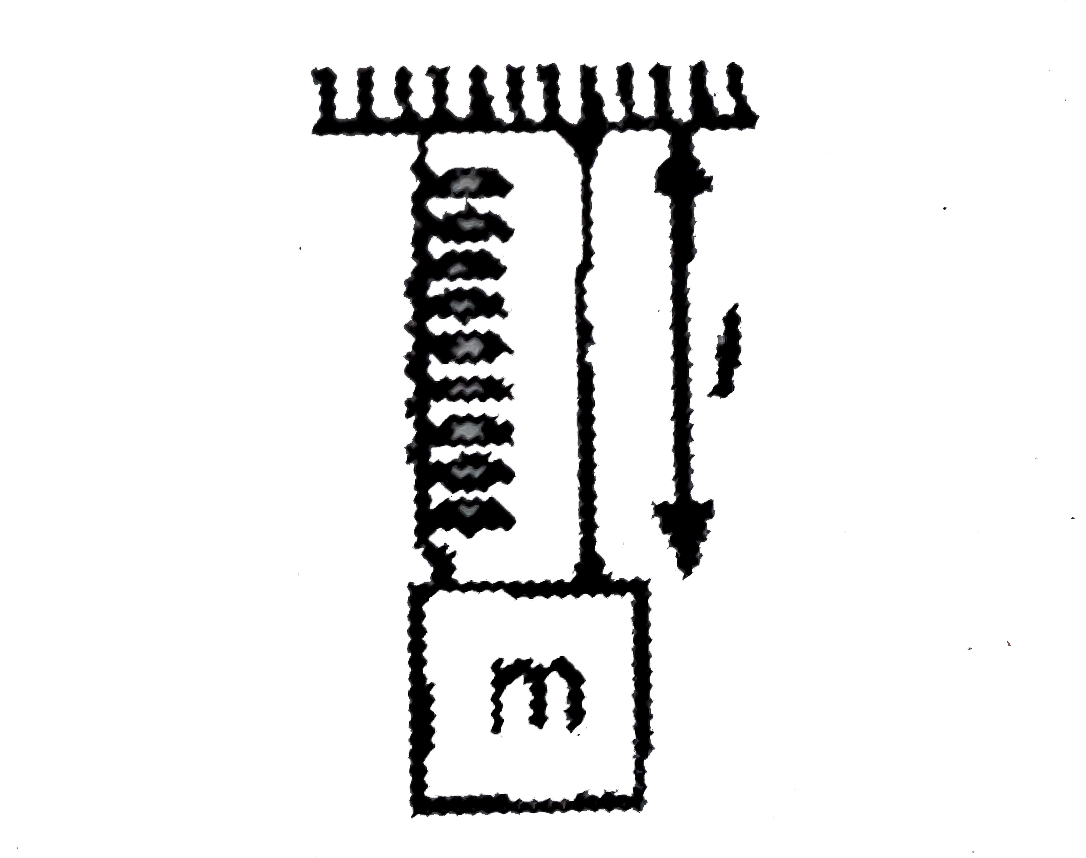
View SolutionThe system shown in the Fig. is in equilibrium. Find the initial acceleration of A, B and C just after the spring 2 is cut.
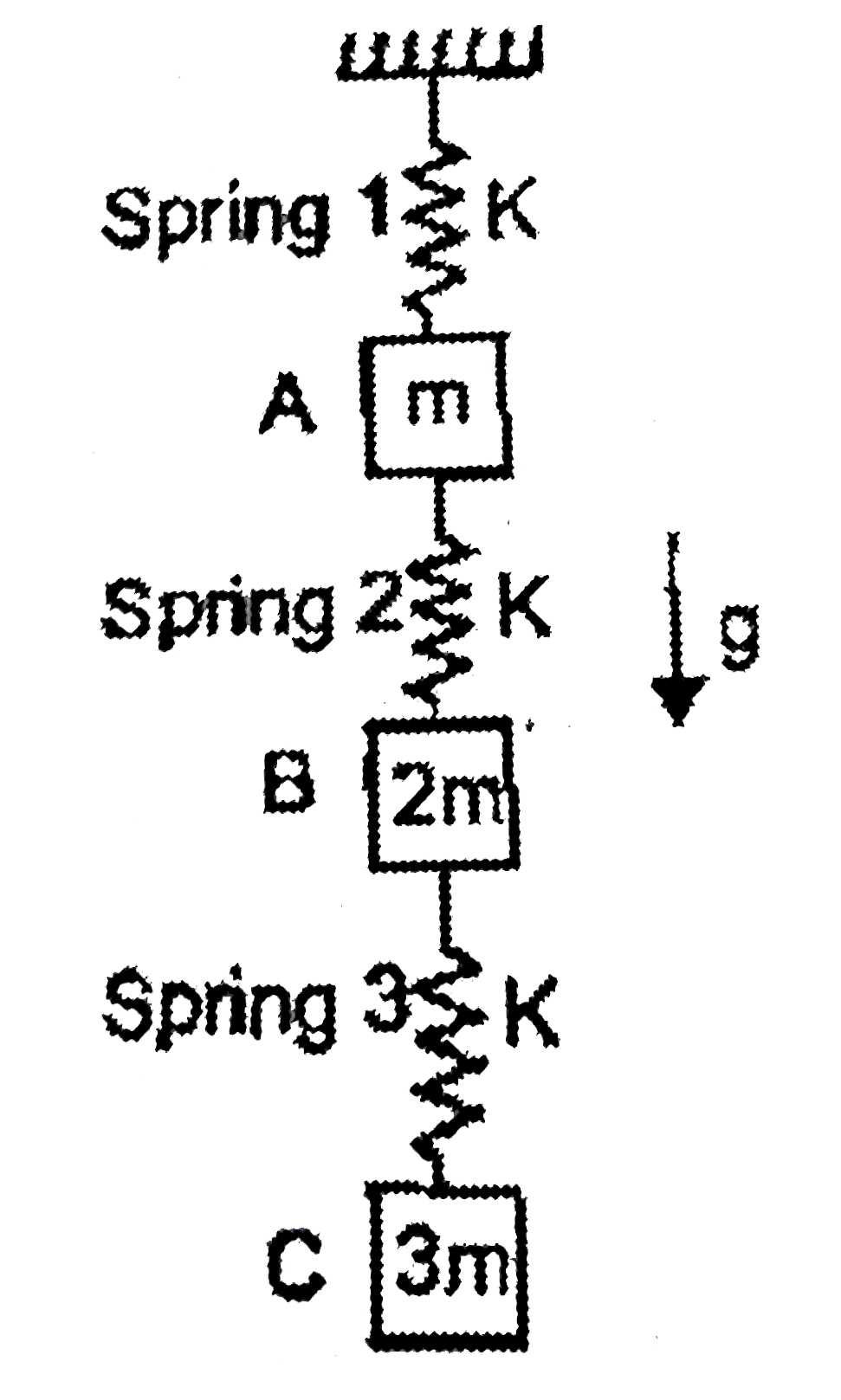
View SolutionThe mass in the fig. can slide on a frictionless surface. The mass is pulled out by a distance `x`. The spring constants are `k_(1)` and `k_(2)` respectively. Find the force pulling back on the mass and orce on the wall.

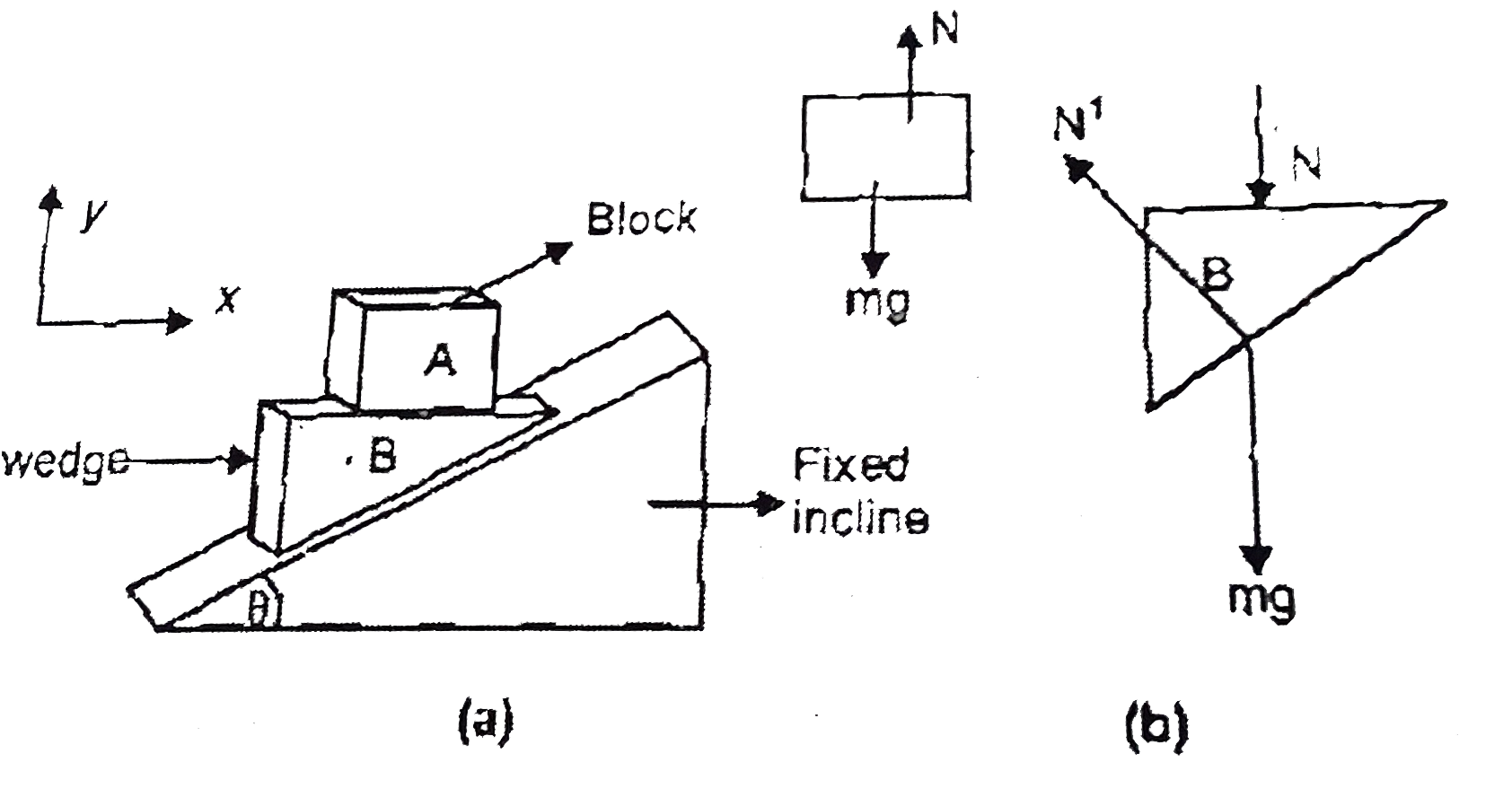
View SolutionBlock A of mass m is placed over a wedge of same mass m. Both the block and wedge are placed on a fixed inclined plane. Assuming all surfaces to be smooth calculate the displacement of the block A in ground frame in `1s`.
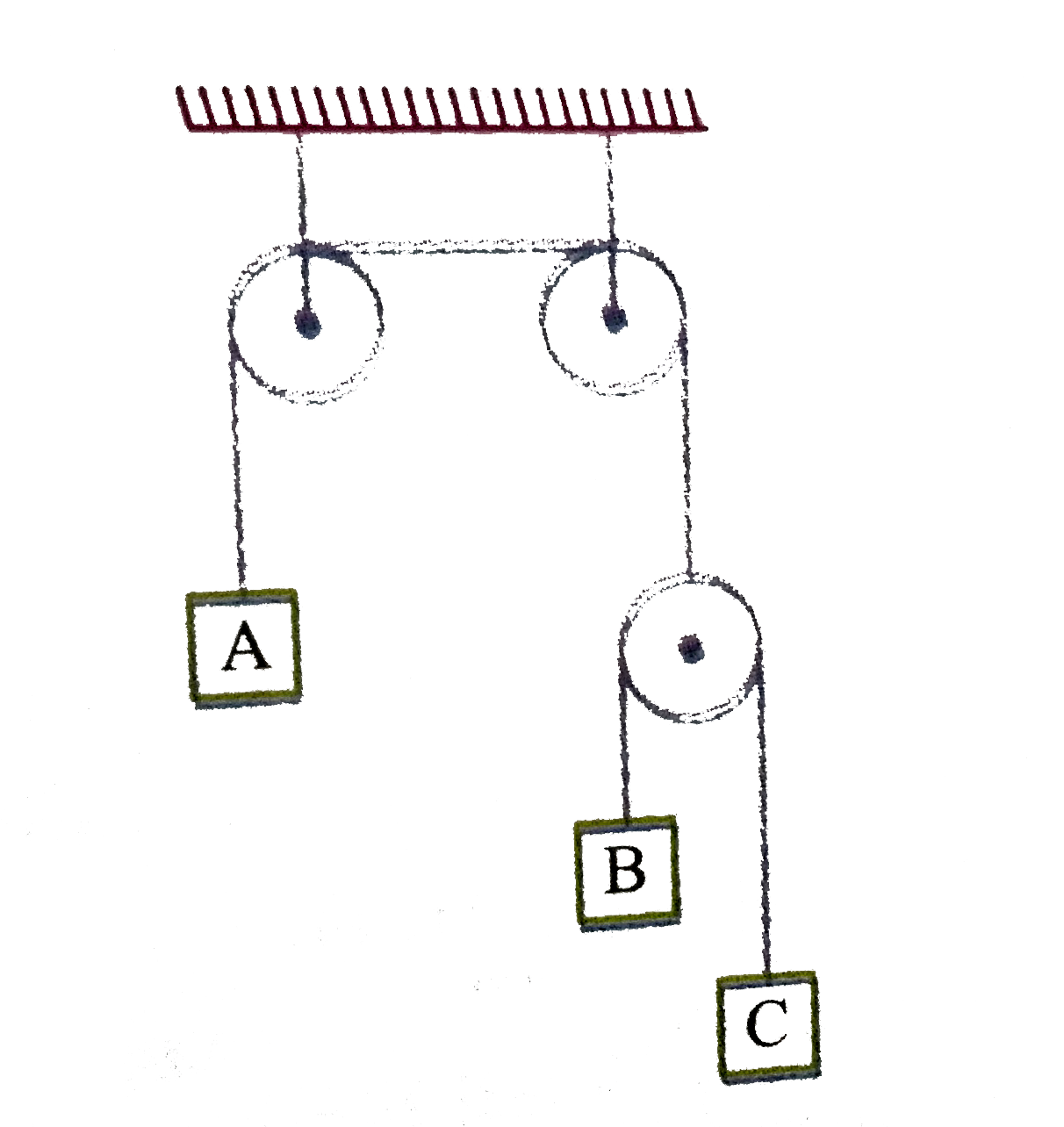
View SolutionIn the pulley system shown in figure the movable pulleys A, B and C are of 1 kg each D and E are fixed pulleys. The strings are light and inextensible find the accelerations of the pulleys and tension in the string.

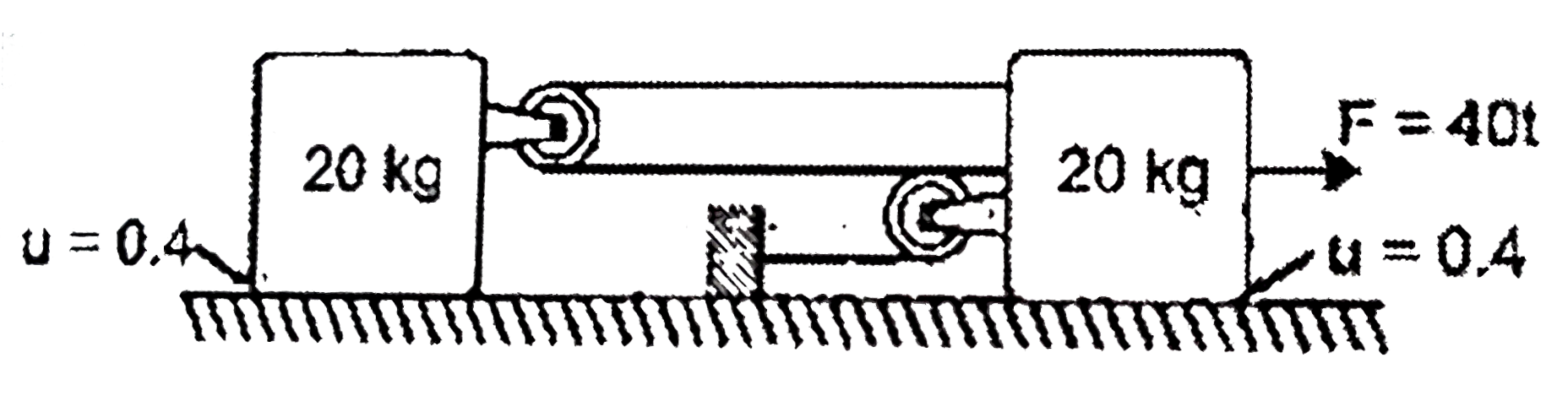
View SolutionTwo identical blocks each having a mass of 20 kg are connected to each other by a light inextensible string as shown and as placed over a rough surface. Pulley are connected to the blocks.
Find acceleration of the blocks after one second after the application of the time varying force of 40 t N, where t is in second.
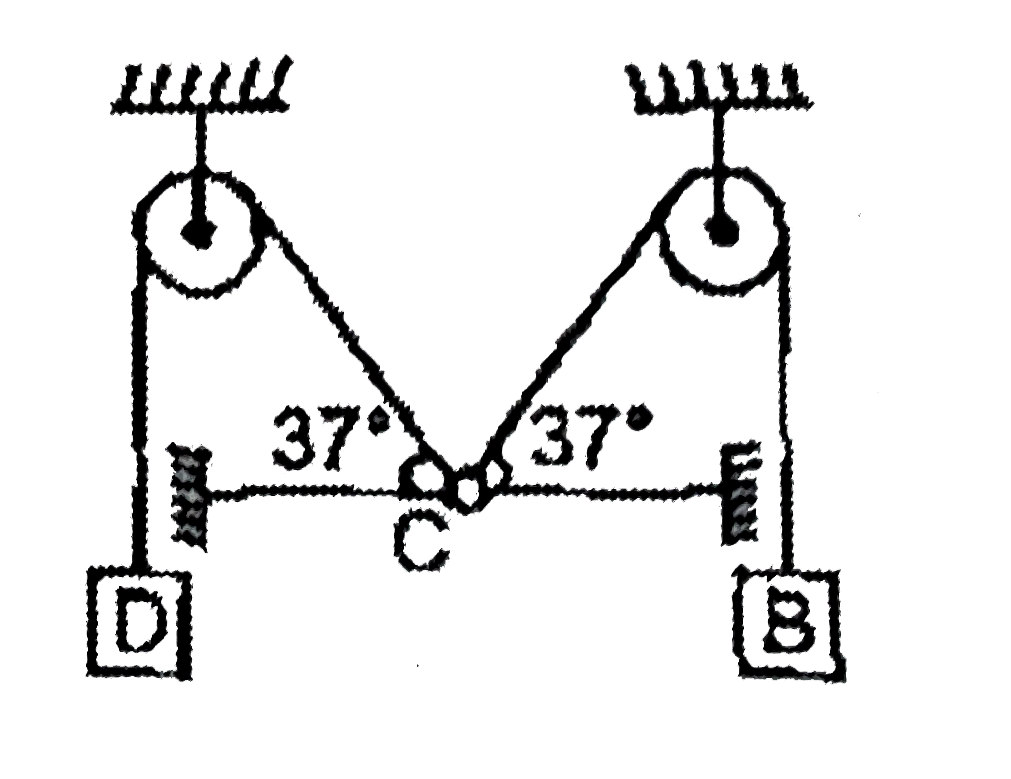
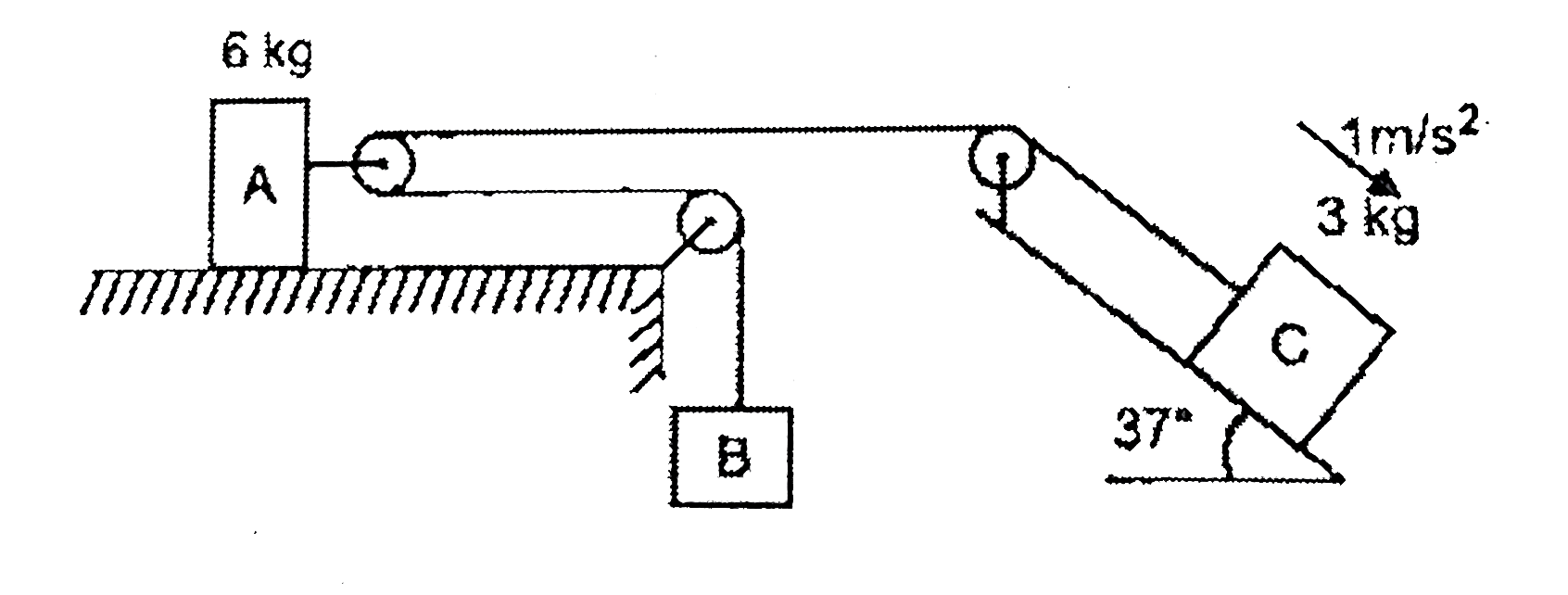
View SolutionThree blocks A, B, & C are arranged as shown. Pulley and strings are ideal. All surfaces are frictionless. If block C is observed moving down along the incline at `1 m//s^(2)`. Find mass of block B, tension in string and accelerations of A. B as the system is released from rest.
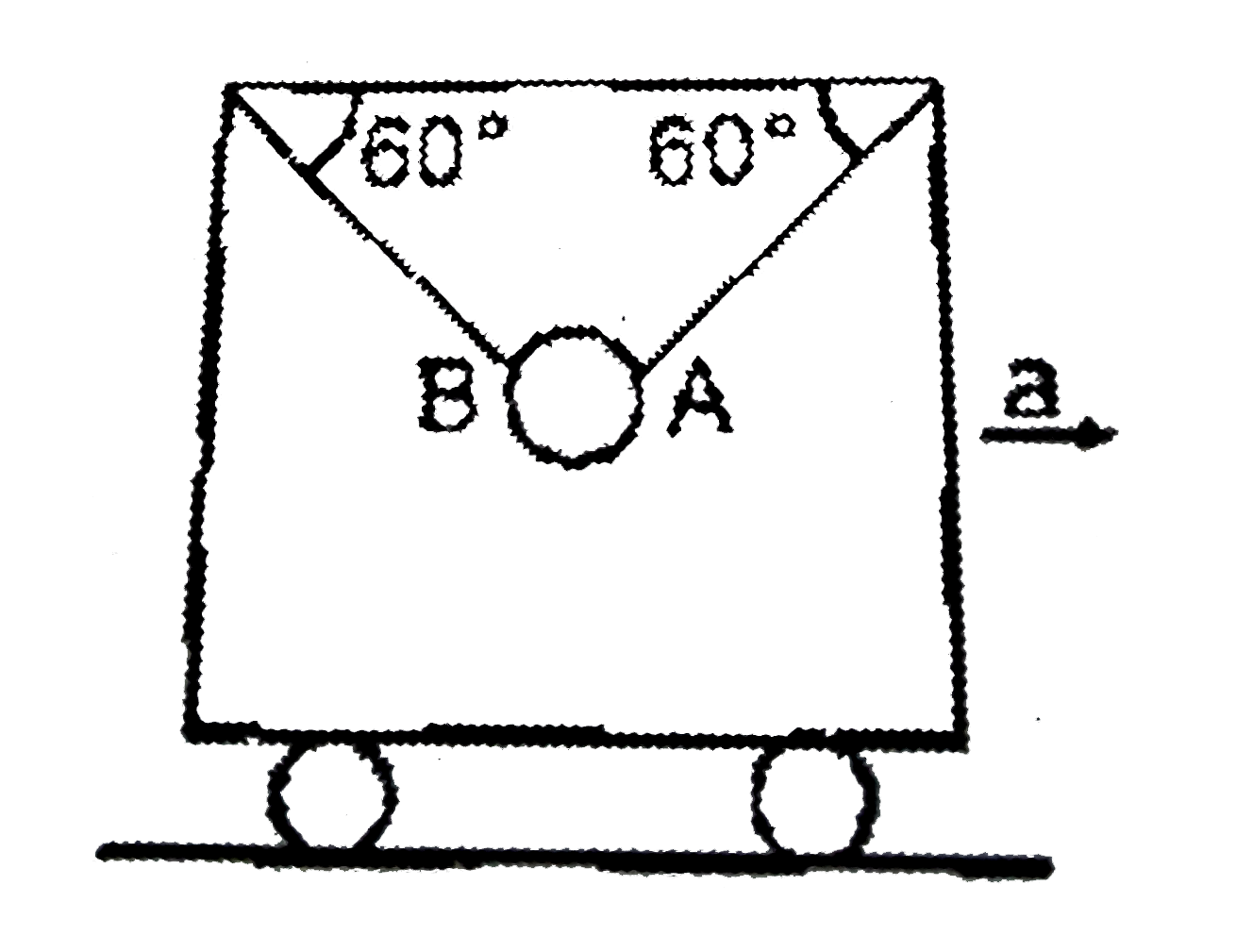
View SolutionThe system shown in the Fig. is given an acceleration 'a' towards left. Assuming all the surfaces to be frictionless, find the force on the sphere.
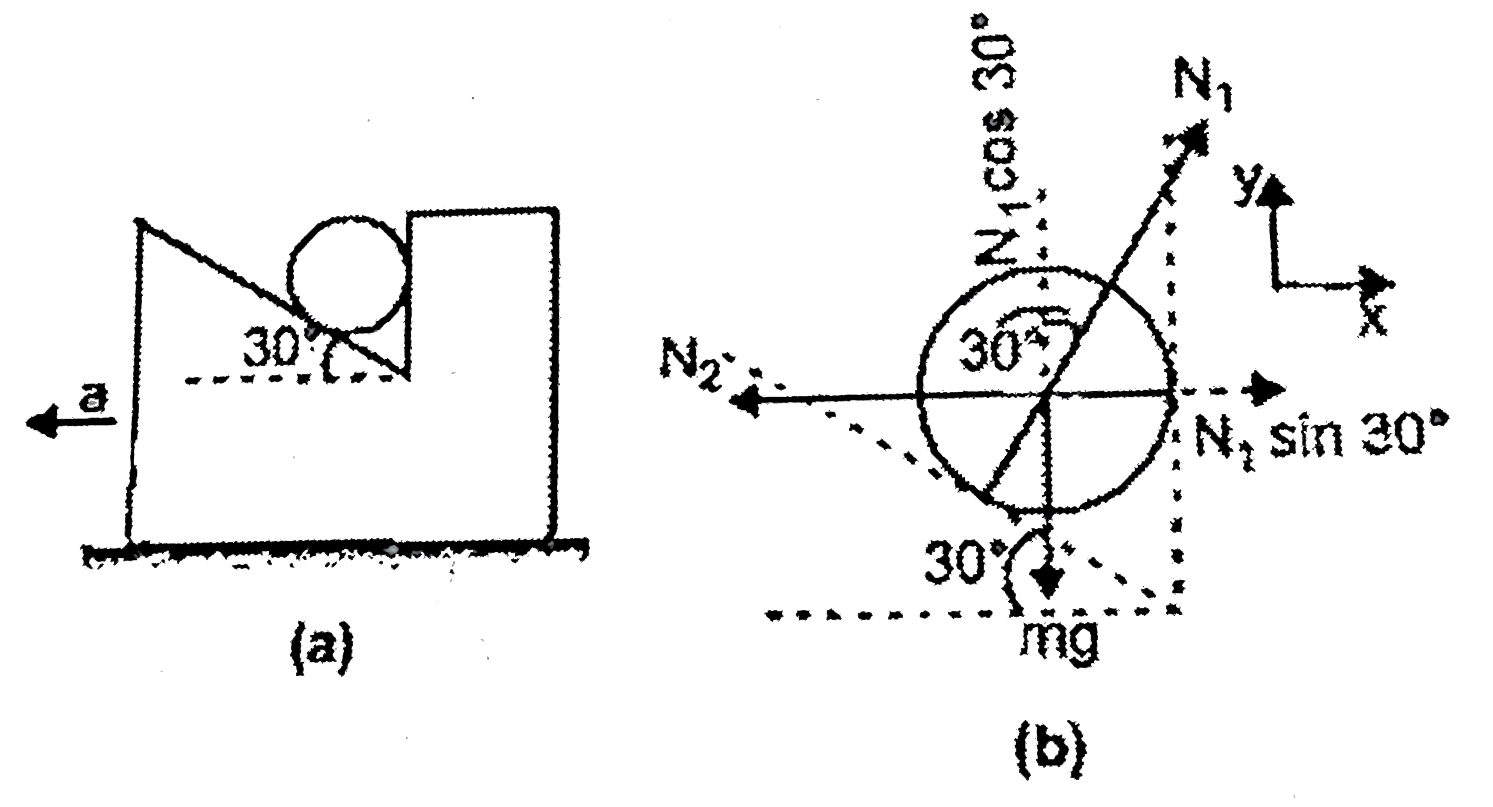
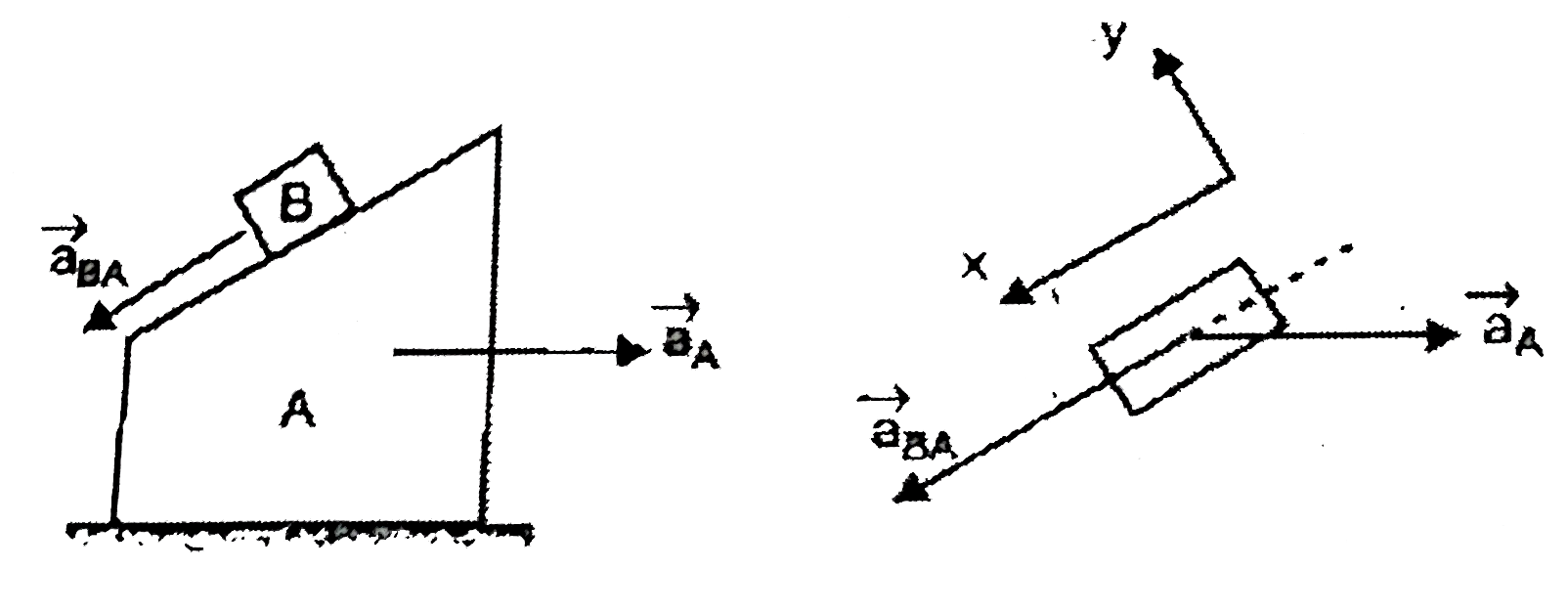
View SolutionThe block B starts from rest and slides on the wedge A which can move on a horizontal surface, Neglecting friction, determine (a) the acceleration of wedge, (b) the acceleration of the block relative to the wedge.
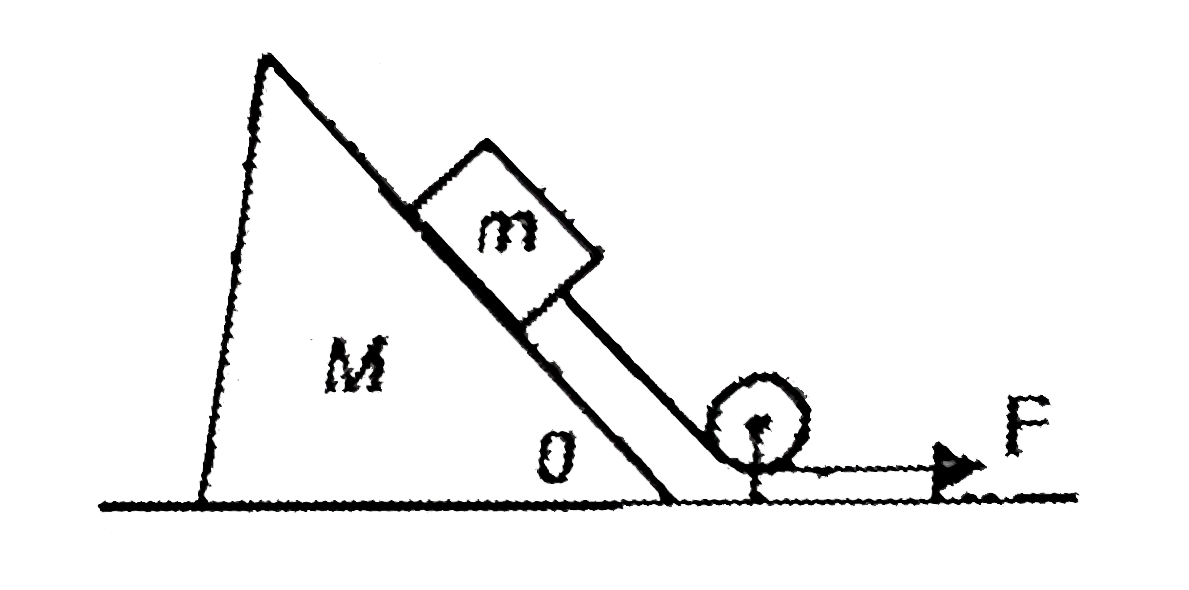
View SolutionIn the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
View SolutionA rod 'A' constrained to move in vertical direction rests on a wedge B, as shown in the Fig. Find the accelerations of rod A and wedge B instantaneously after system is released from rest, neglecting friction at all the contact surfaces.
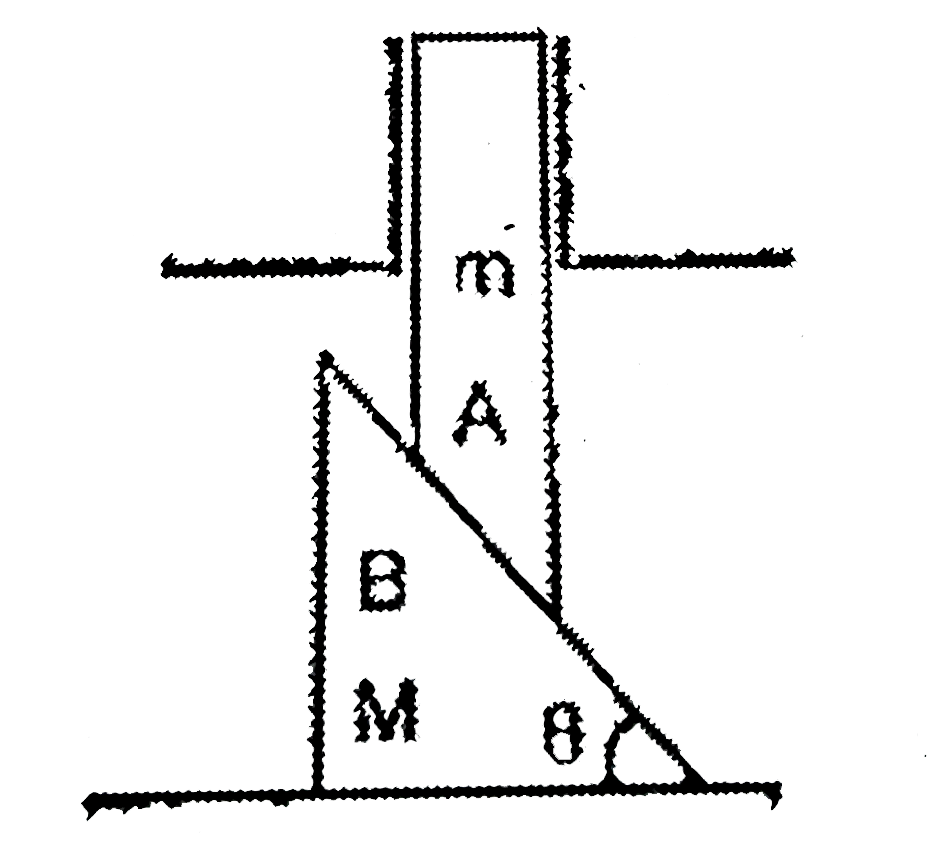
View SolutionA block weighing 20 N rests on a horizontal surface. The: coefficient of static friction between block and surface is 0.40 and the coefficient of kinetic friction is 0.20.
( a) How large is the friction force exerted on the block?
(b) How great will the friction force be if a horizontal force of 5 N is exerted on the block?
(c) What is the minimum force that will start the block in motion?
(d) What is the minimum force that will keep the block in motion once it has been started?
(e) If the horizontal force is 10 N, what is the friction force?
View SolutionA wedge of mass M makes an angle `theta` with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
View SolutionFind the acceleration of the block and magnitude and direction of frictional force between block A and table, if block A is pulled towards Left with a force of 50 N.

View SolutionThe 10 kg block is resting on the horizontal surface when the force 'F is applied to it for 7 second. The variation of 'F with time is shown. Calculate the maximum velocity reached by the block and the total time 't' during which the block is in motion. The coefficient of static and kinetic friction are both, 0.50.
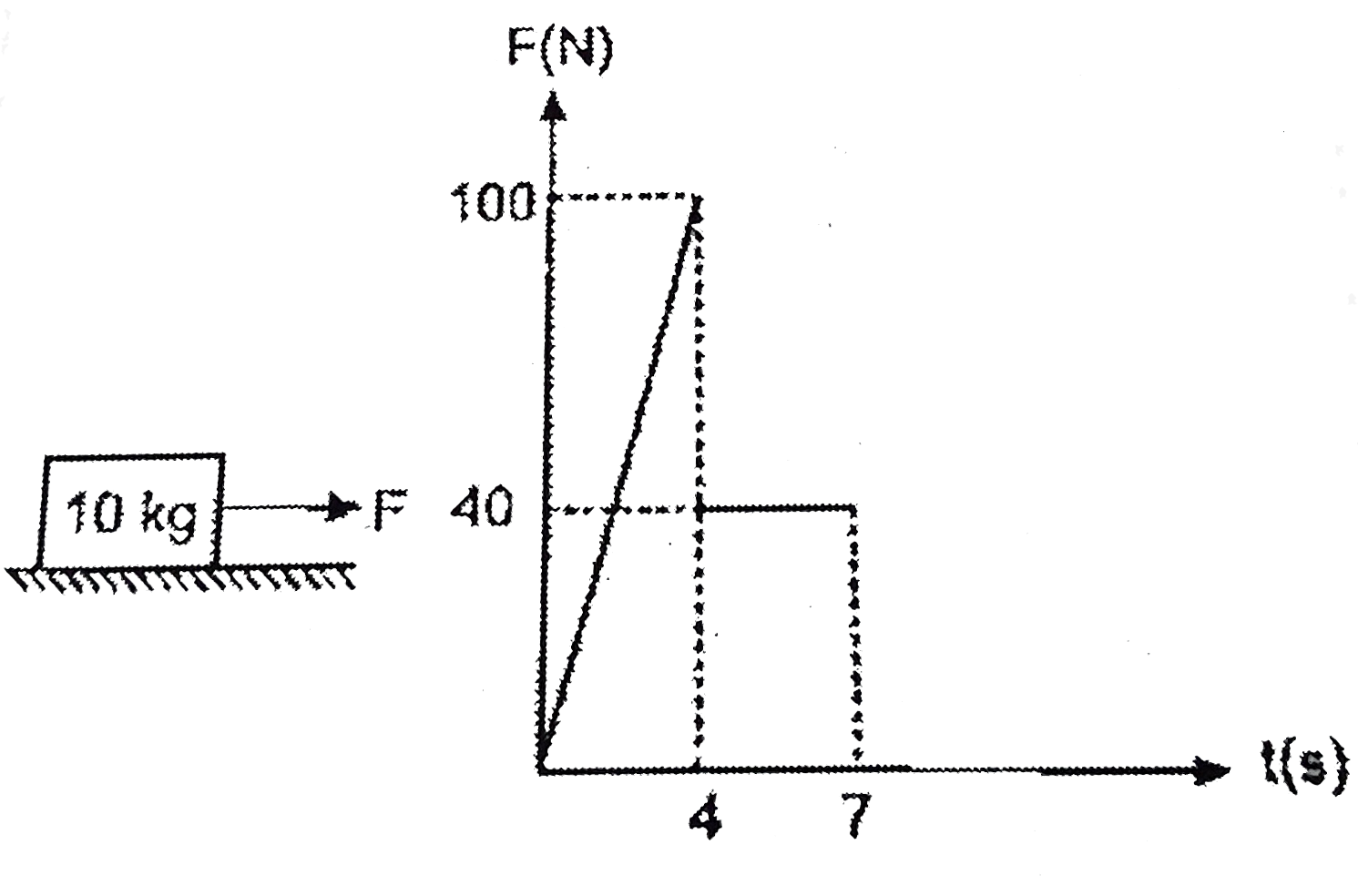
View SolutionA force `F = 20 N` is applied to a block (at rest) as shown in figure. After the block has moved a distance of `8 m` to the right, the direction of horizontal component of the force F is reversed. Find the velocity with which block arrives at its starting point.
 .
.
View SolutionFind the contact force on the 1 kg block.

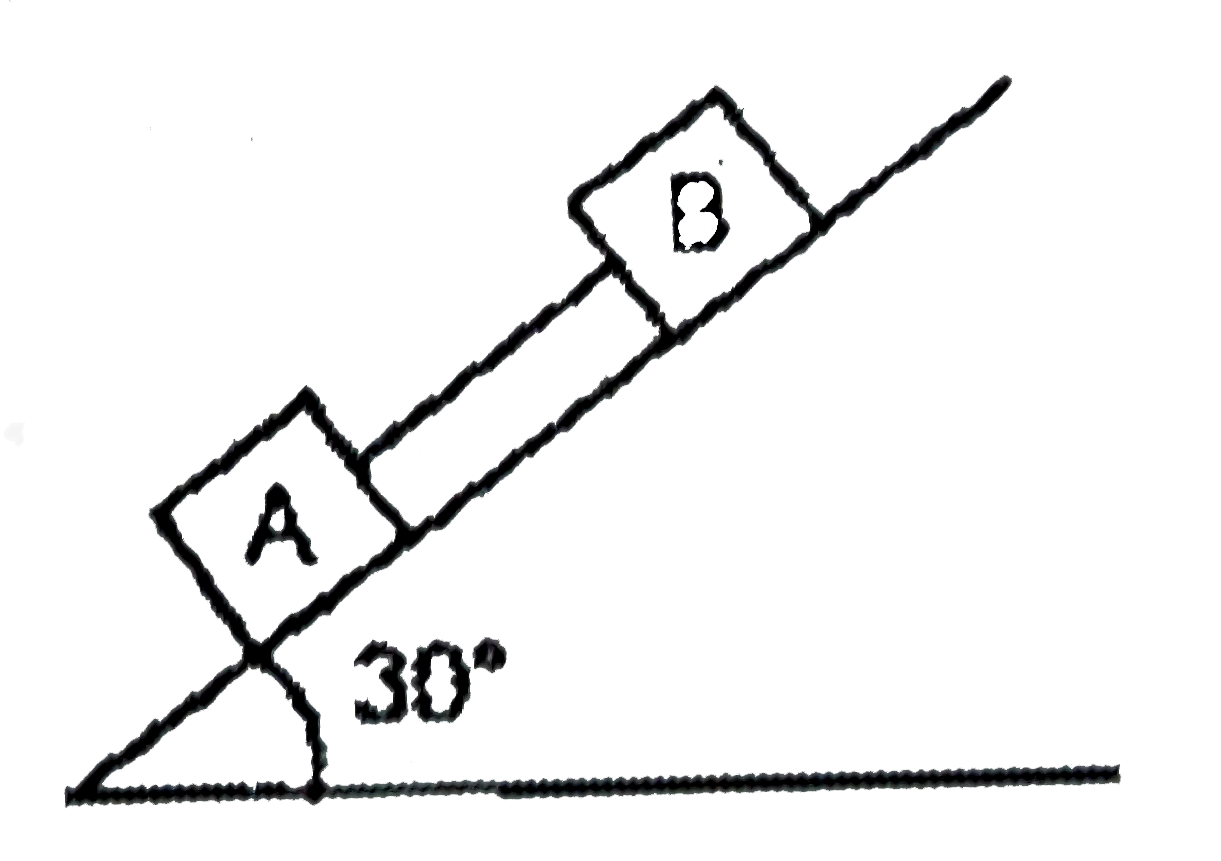
View SolutionBlocks A and Bin the Fig. 2E.46 .(a) are connected With a string of negligible mass. The masses are placed on an inclined plane of inclination `30^(@)` as shown inFig. 2E.46 (a) . If A and B each have mass m and `mu_(A)=0` and `mu_(R)=sqrt(2/3)`, where `mu_(A)` and `mu_(B)` are the coefficient of friction between plane and the bodies respectively, calculate the acceleration of the system and tension in the string.
View SolutionIn the Fig. shown a time dependent force F expressed as `F=kt` is applied on a block of mass 5 kg. Coefficient of static and kinetic friction is `mu_(s)=0.4` and `mu_(k)=0.3`. Motion begins when `t=2` sec draw a acceleration vs time graph for block. `(m=5 kg, mu_(s)=0.4, mu_(k)=0.3)`

View Solution`m=20 kg, mu_(s)=0.5`, find friction on block.

View SolutionFind `theta` at which slipping will start. `mu_(s)` is coefficient of static friction. (Angle of repose)

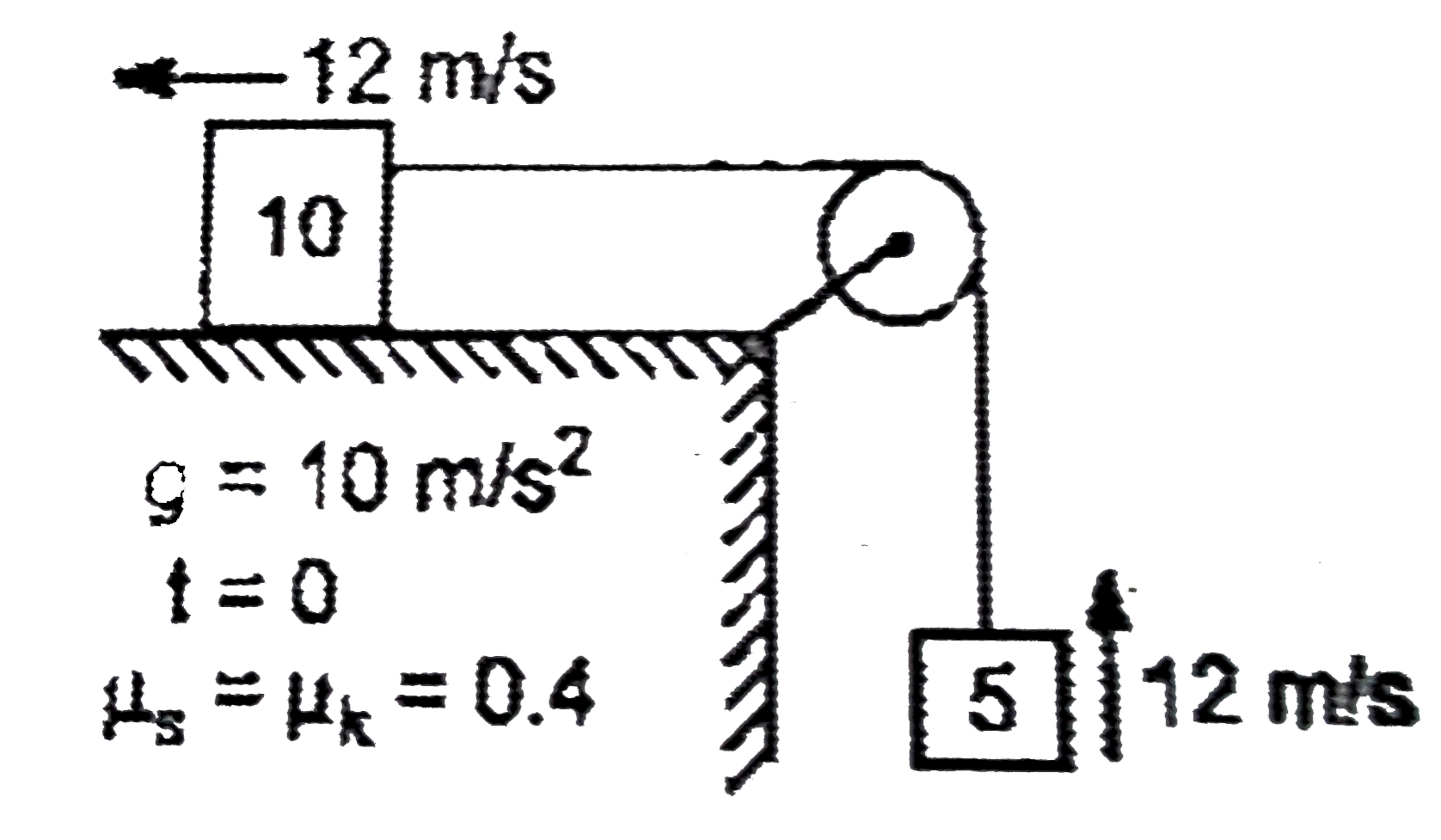
View SolutionBlocks are given velocities as shown at `t=0`, find velocity and position of 10 kg block at `t=1` and `t=4`.
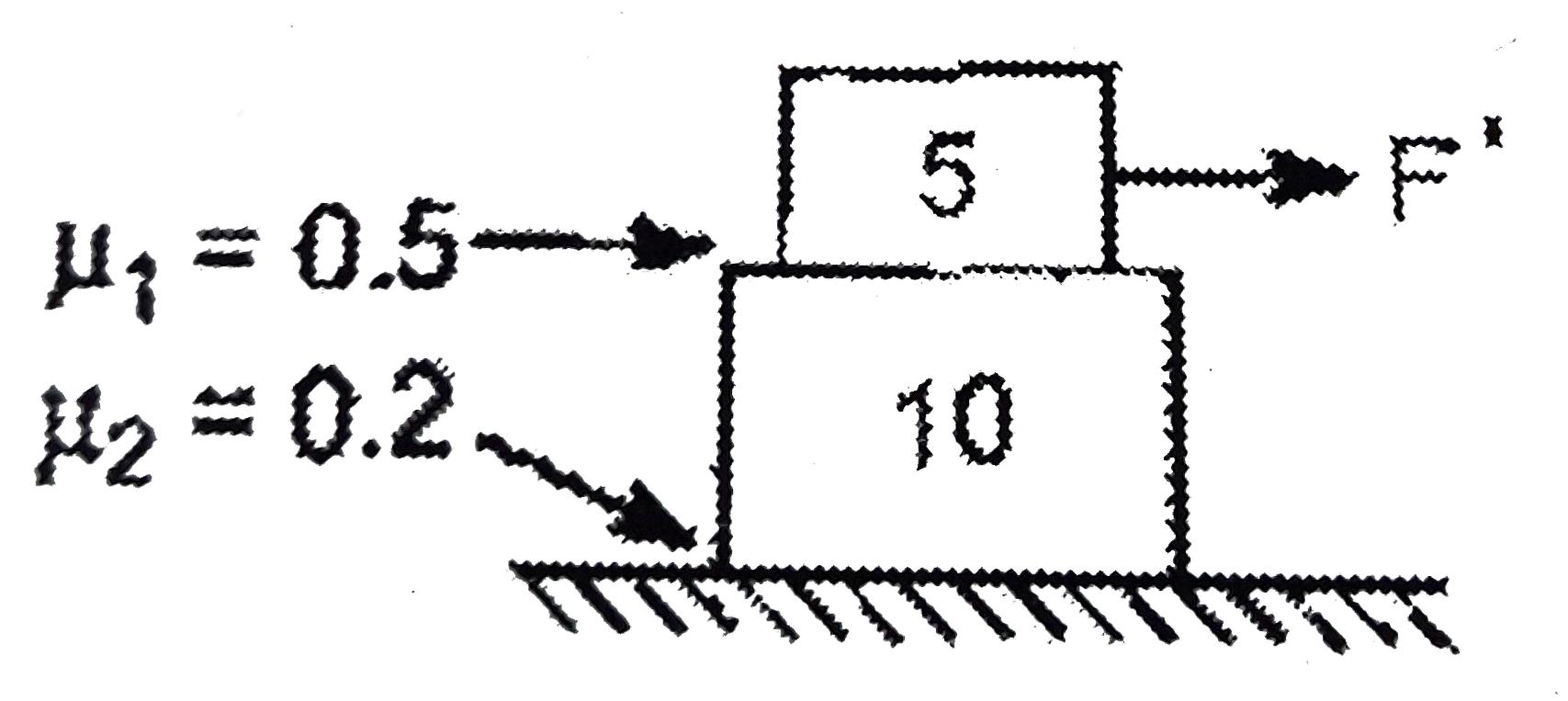
View SolutionFind acceleration of blocks `F=40 N`
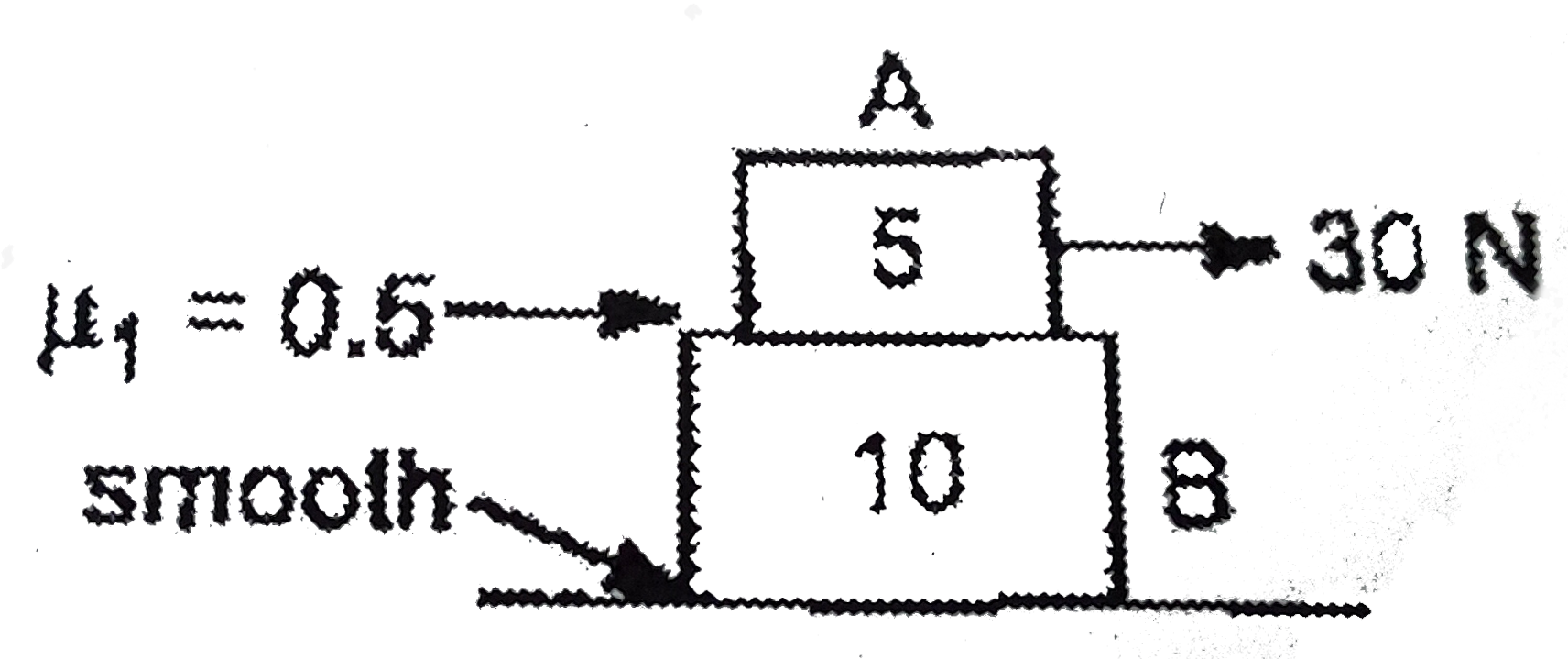
View SolutionFind Force acting on object B.
View SolutionIf a force of 60N is applied on the upper block will the two blocks move together with an acceleration of `4 m/s^2`. If not, find their acceleration.
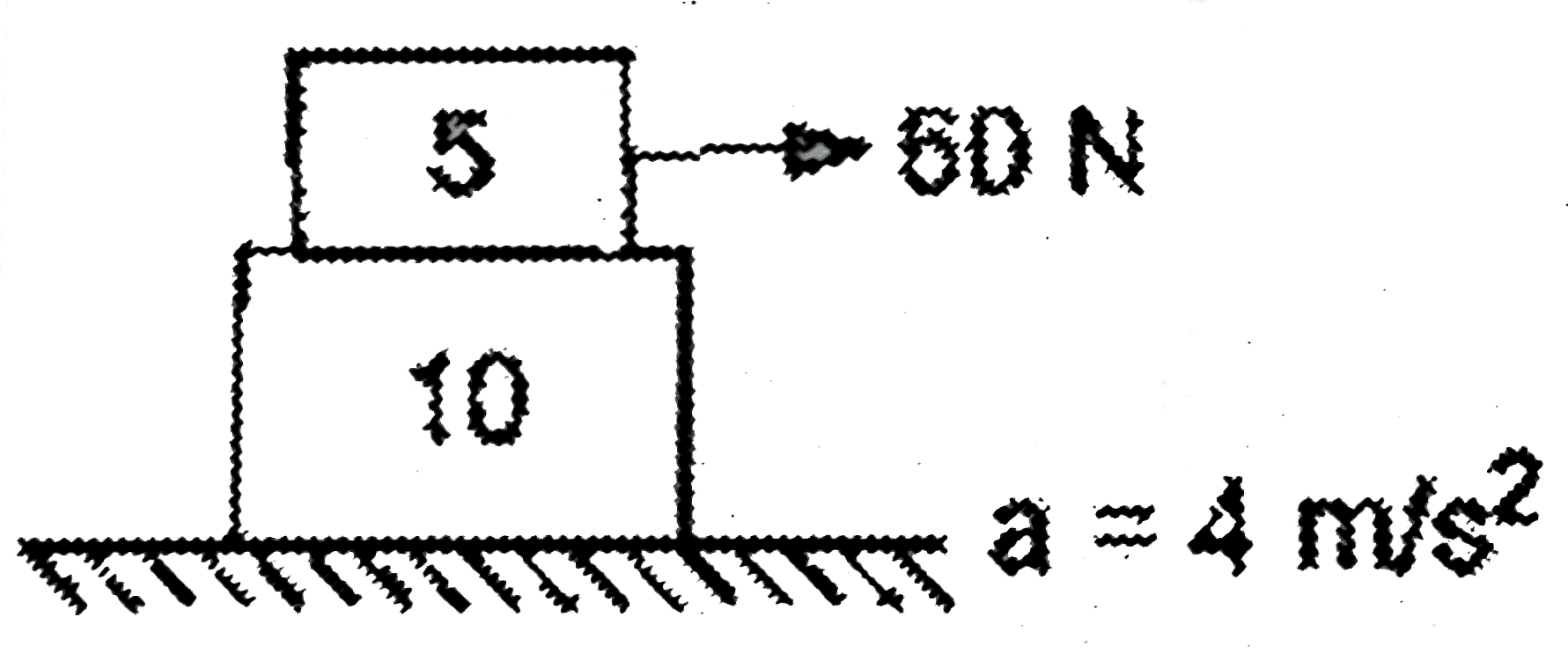
View SolutionFind maximum force for which they can move together
View SolutionCoefficient of friction between 5 kg and 10 kg block is 0.5. If friction between them is 20 N. What is the value of force being applied on 5 kg. The floor is frictionless
View SolutionAn object is given a quick push up an inclined plane. It slides up and then comes back down. It is known that the ratio of the ascent time `(t_("up"))` to the descent time `(t_("dawn"))` is equal to the coefficient of kinetic friction `(mu)`. Find the angle `theta` that the inclined plane makes with the horizontal Find also the range of `mu` for which the situation described is possible. Assume. that the coefficints of static and kinetic friction are equal.
View SolutionA time varying for `F=10 sqrt(2) t` starts acting on the 3 kg block lept on a rough horizontal surface `(mu=0.2)` at `t=0`. Find
(a) the moment of time when the blocks leaves the surface
the moment of time when the horizontal motion begins.

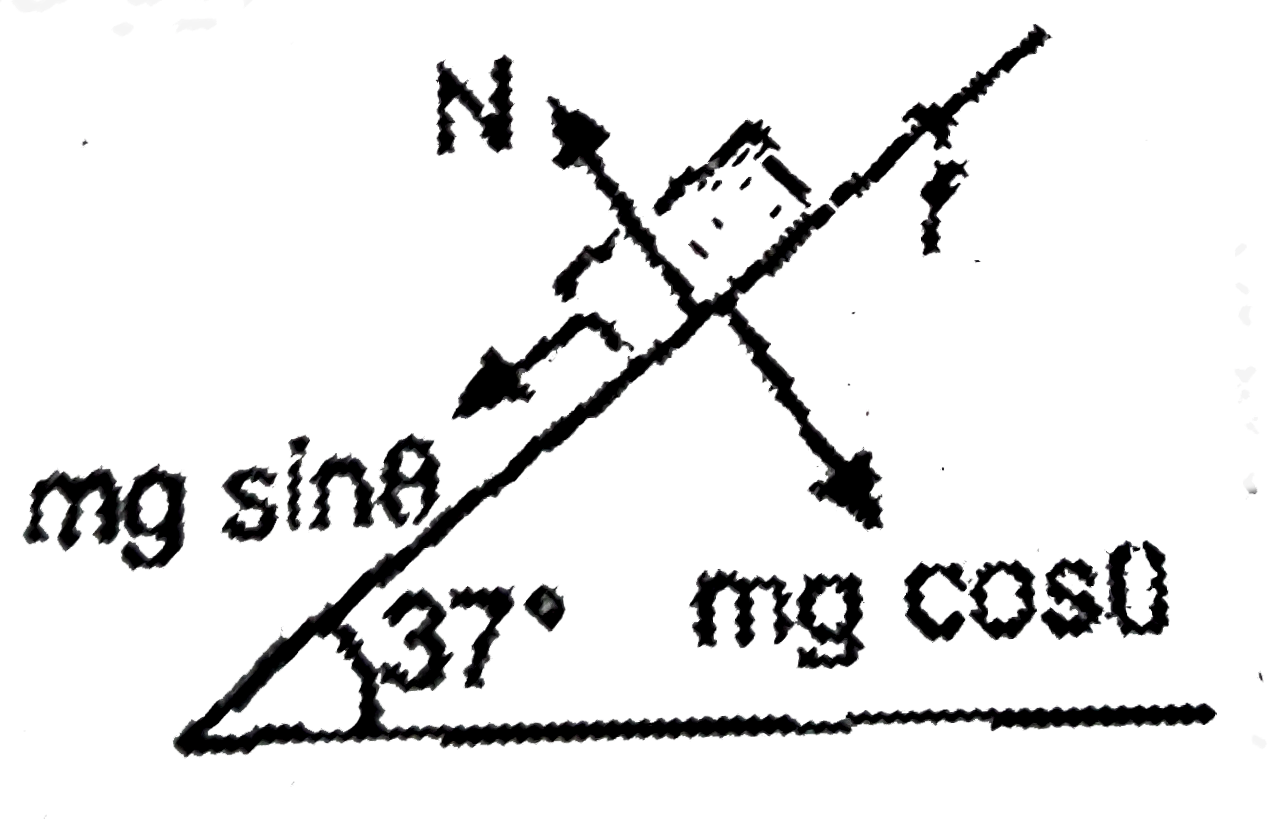
View SolutionA block of mass 3 kg slides on a rough fixed inclined plane of `37^(@)` angle having coefficient of friction 0.5. find the resultant force exerted by plane on the block.
View SolutionA car has headlight which can illuminate a horizontal straight road in front upto a distance `l`. If coefficient of friction between tyres & road is `mu`. Find the maximum safe speed of the car during a night drive neglect the reaction time of the driver.
View SolutionA block of mass 2 kg is placed on the floor `(mu=0.4)`. A horizontal force of 7 N is applied on the block. The force of friction between the block & floor is `f_(s)`. Find the `f_(s)`.
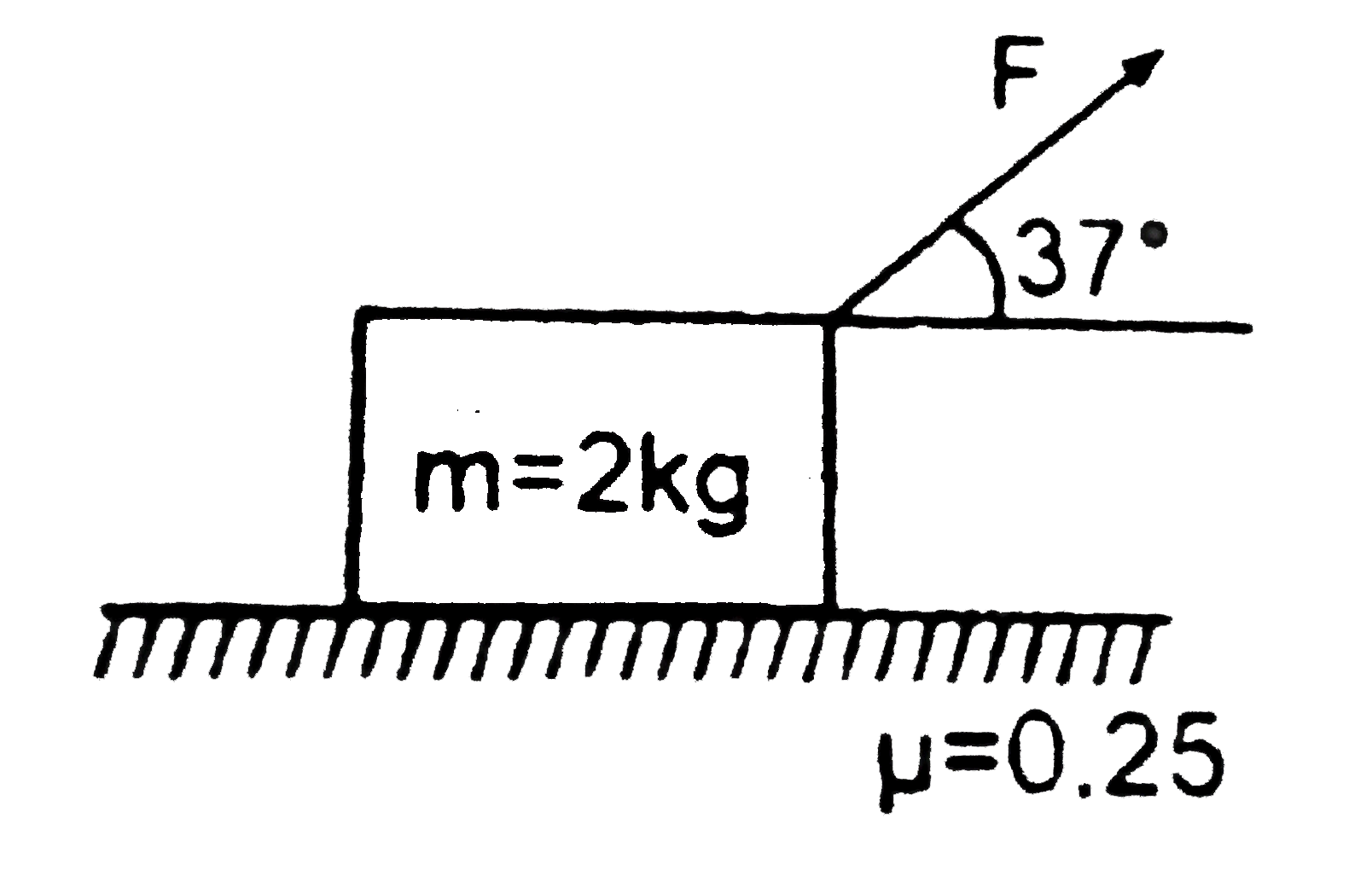
View SolutionIn Fig block 1 is placed on top of block `2` .Both of then have a mass of `1 kg` The coefficient of friction between block 1 and 2 are `mu_(s) = 0.75` and `mu_(k) = 0.60` The table is frictionless A force `p//2` is applied on block `1 ` in the left and force `P` on block `2` to the right .Find the minimum value of `p` such that sliding accore between the two blocks

View SolutionA block of mass `m` rests on a rough floor . The coefficient of friction between the block and the floor is `mu`
a. Two boys apply force `P` at an angle `theta` to the horizontal. One of them pushes the block , the other one pulls. Which one would reqire less efferts to cause impending motion of the block?
b. What is the minimum force required to move the block by pulling it ?
c. Shown that the block is pushes at a certain angle `theta _(0)` it cannot be moved fro whatever the value of `P` be
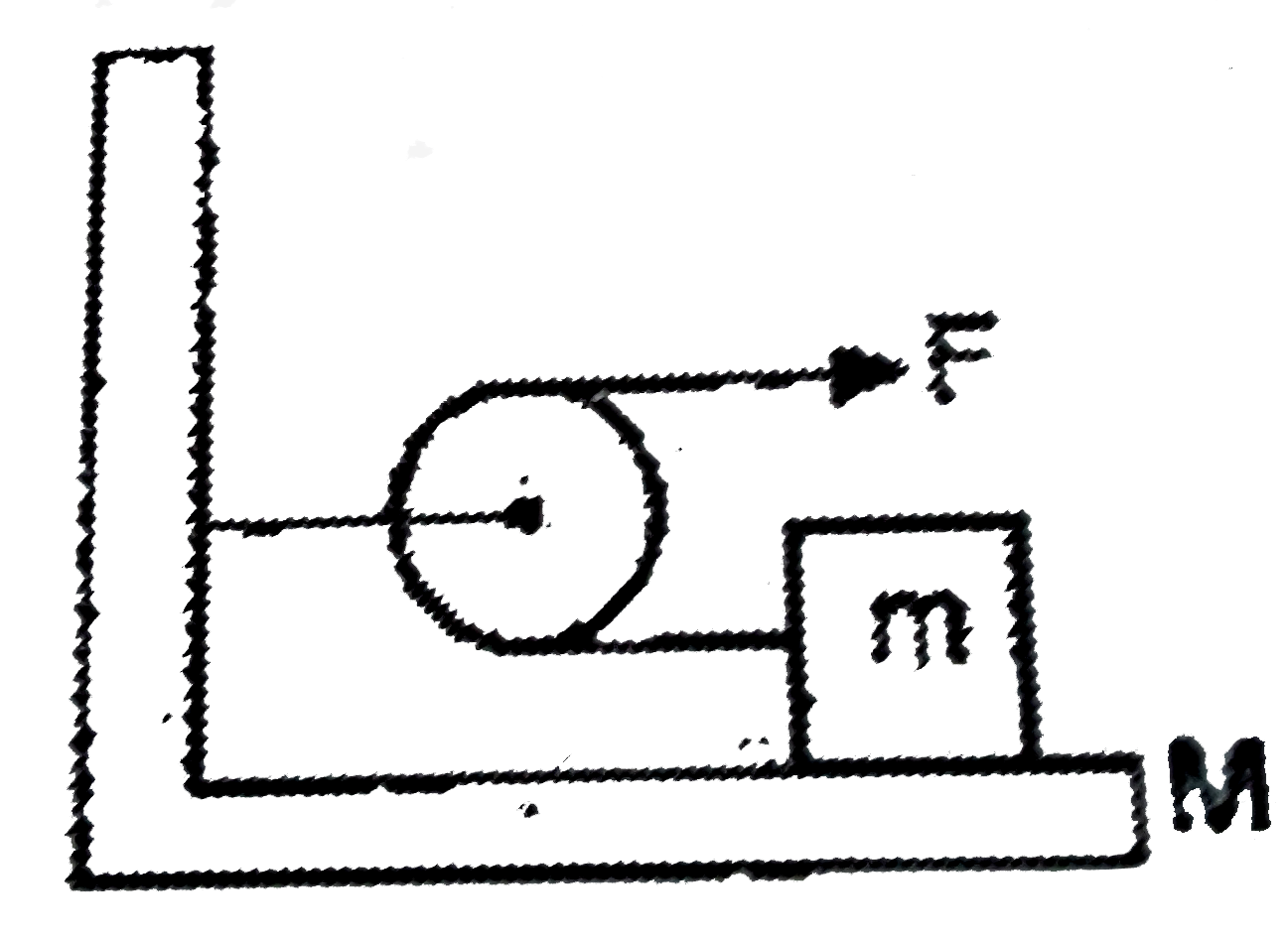
View SolutionA block of mass m rests on a bracket of mass M. The coefficients of friction between block and bracket are `mu_(s)` and `mu_(k)` . The bracket rests on a frictionless surface. What is the maximum force F that can be applied if the block is not to slide on the bracket?
View SolutionA block of mass `m` is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is `mu`
For what range of value of `p` , the block remain in static equilibrium ?

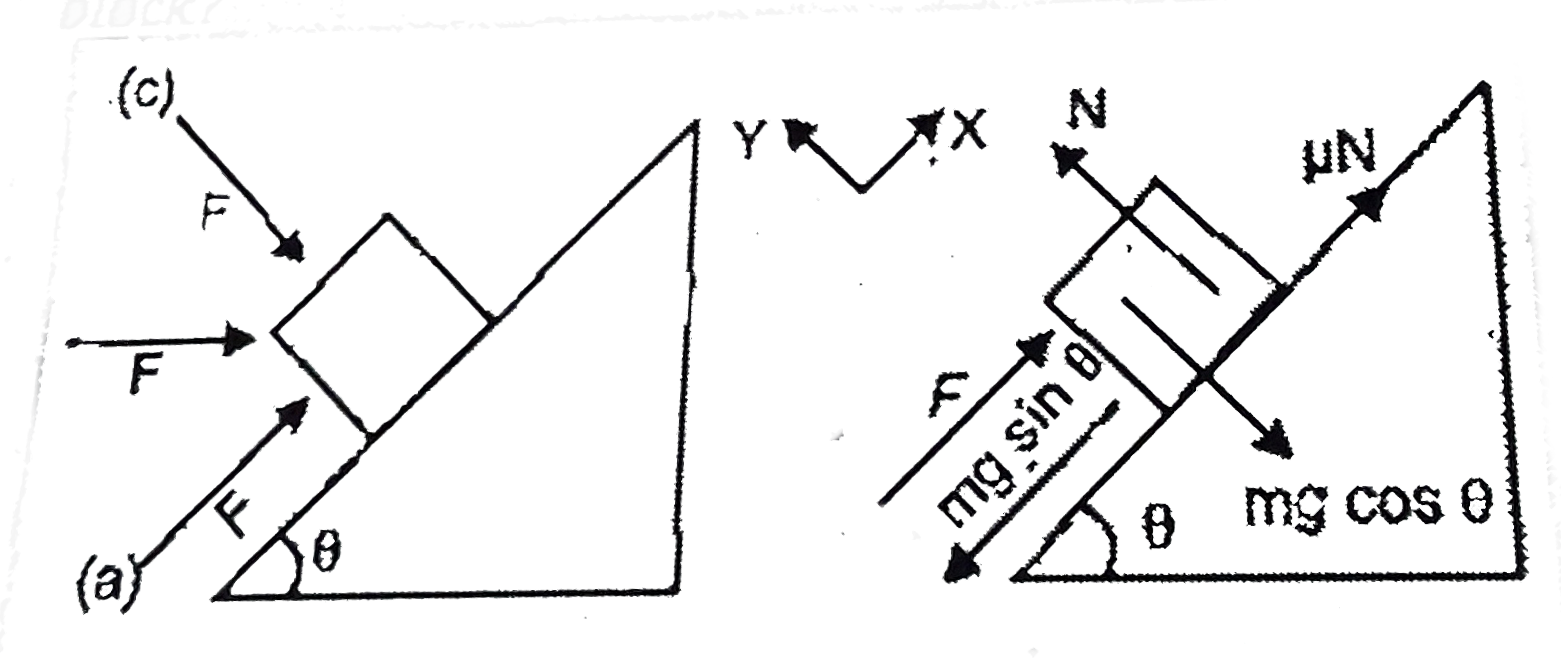
View SolutionA block is kept on a rought incline whose angle of inclination is greater than angle of repose.
(a) Find the minimum and maximum force F applied parallel to incline that will keep it in equilibrium.
(b) What is the required force if it is applied normal to the incline?
(c) What is the range of F if it is applied horizontally on the block?
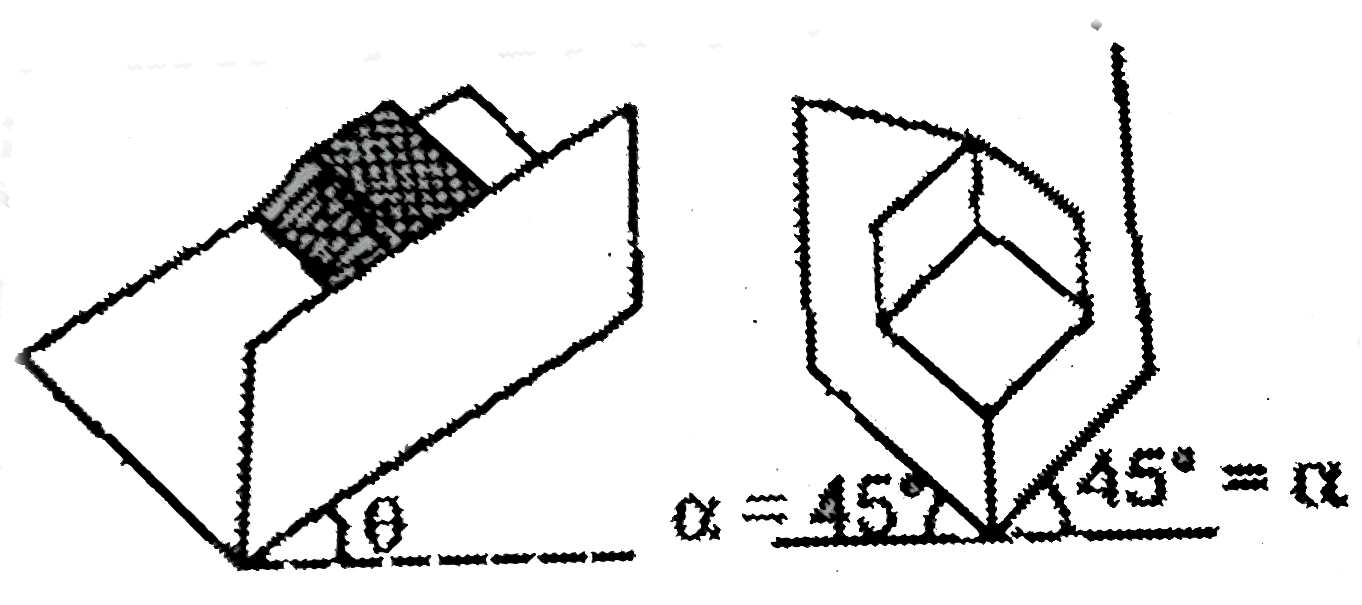
View SolutionA wooden block slides down the right angle channel as shown in Fig. The channel is inclined at an angle `theta` w.r.t. the horizontal . The angle `alpha` is `45^(@)`, i.e., the channel is oriented symmetrically with the vertical. IF the coefficient of friction between the block and the channel is `mu_(k)`, find the acceleration of the block.
View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle `theta` with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is `mu_(s)`. Find the minimum and maximum value of 'm' so that the system is at rest.

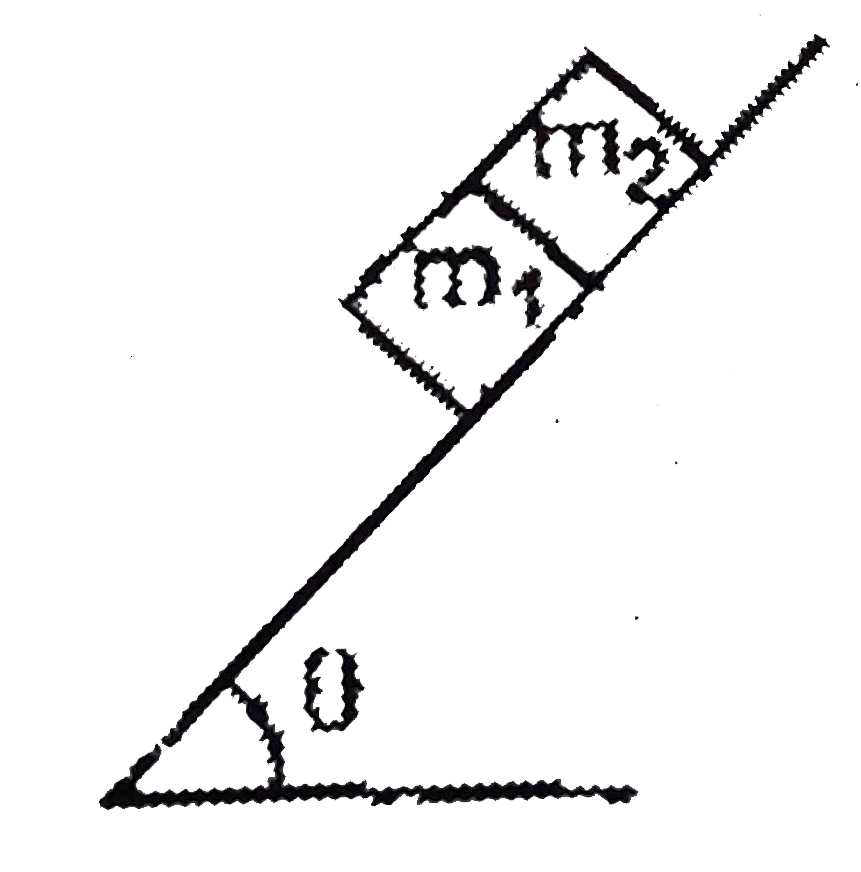
View SolutionTwo blocks are kept an incline in contact with each other. Masses of blocks are `m_(1)` and `m_(2)` and coefficients of friction are `mu_(1)` and `mu_(2)` respectively. The angle of inclination is `theta`. Determine
(a) acceleration of block, and
(b) force F with which the blocks press against each other
View SolutionFour blocks are arranged on a smooth horizontal surface as shown. The masses of the blocks are given (see the diagram). The coefficient of static friction between the top and the bottom blocks is `mu_(s)`. What is the maximum value of the horizontal force F, applied to one of the bottom blocks as show, thilt makes all four blocks move with the same acceleration ?

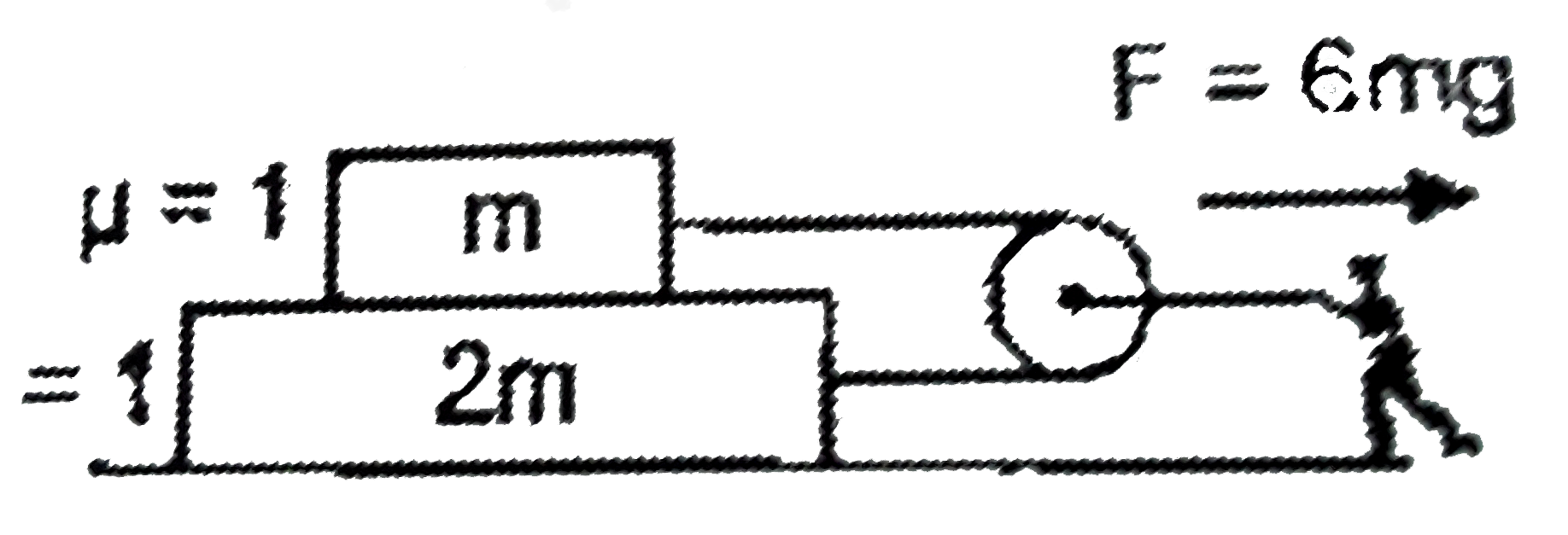
View SolutionA block of mass m rests on top of a block of mass 2m which ls kept on a table. The coefficient of kinetic friction between all surfaces is `mu = 1 A` massless string is connected to each mass and wraps halfway around a massless pulley, as shown. Assume that you pull on the pulley with a force of 6 mg. What ls the acceleration of your hand ?
View SolutionA 4 kg block ls placed on top of a long .12 kg block, which is accelerating along a smooth horizontal table at `a= 5.2 m//s^(2)` under application of an external constant force. Let minimum, coefficient of friction between the two blocks which will prevent the 4 kg block from sliding is `mu`, and coefficient of friction between blocks ls only half of this minimum value. of, (i.e., `mu//2`). Find the amount of heat (in joules) generated due to sliding between the two blocks during the time in which. 12 kg block moves 10 m starting from rest

View SolutionGiven the setup shown in Fig Block `A, B` and `C` have masses `m_(A)= M` and `m_(B) =m_(C) = m`. The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block `B` and the support table, but there is friction between blocks `B` and `C`, denoted by a given coefficient `mu`

a . In terms the given find (i) the acceleration of block `A` and `B`
b. Suppose the system is released from rest with block `C` near the right end of block `B` as shown in the above figure. If the the length `L` of block `B` is given, what is the speed of block `C` as it reached the left end of block `B` ? Tear the size of `C` as small
c. If the mass of block `A` is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.
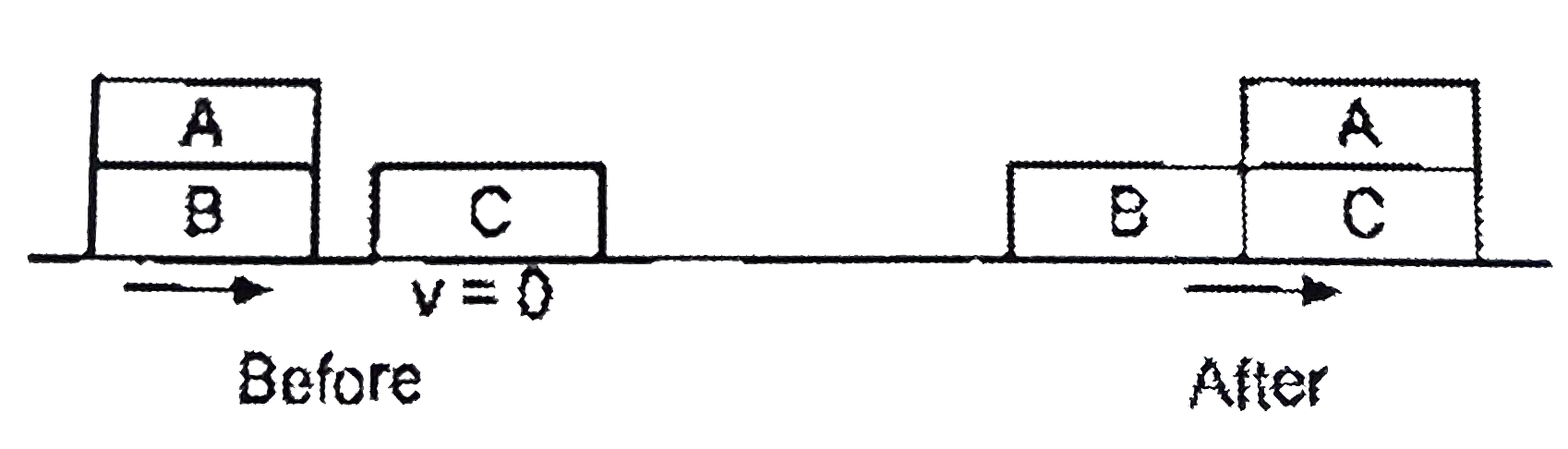
View SolutionBoard A is placed on board B as shown. Both boards slide, without moving with respect to each other, along a frictionless horizontal surface at a speed 6 m/ s. Board B hits a resulting board C "head·on". After the collision, board B and C stick together and board A slides on top of board C and stops its motion relative to C in the position shown on the diagram. What is the length (in m) of each board? All three boards have the same mass, size and shape. The coefficient of kinetic friction between boards A and C and between board A & B is 0.3
View SolutionA side view of a simplified form of vertical latch B is as shown. The lower member A can be pushed forward in its horizontal channel. The sides of the channels are smooth, but at the inteifaces of A and B, which are at `45^(@)` with the horizontal, there exists a static coefficient of friction `mu= 0.4`. What is the' minimum force F (in N) that must be applied horizontally to A to start motion of the latch B if it has a mass `m = 0.6` kg question

View SolutionA carriage of mass M and length l is joined to the end of a slope as shown in the Fig 2E.81 (a). A block of mass m is released from the slope from height h. It slides till end of the carriage (The friction between the body and the slope and also friction between carriage and horizontal floor is negligible) Coefficient of friction between block and carriage is `mu`. Find ,minimum h in the given terms.
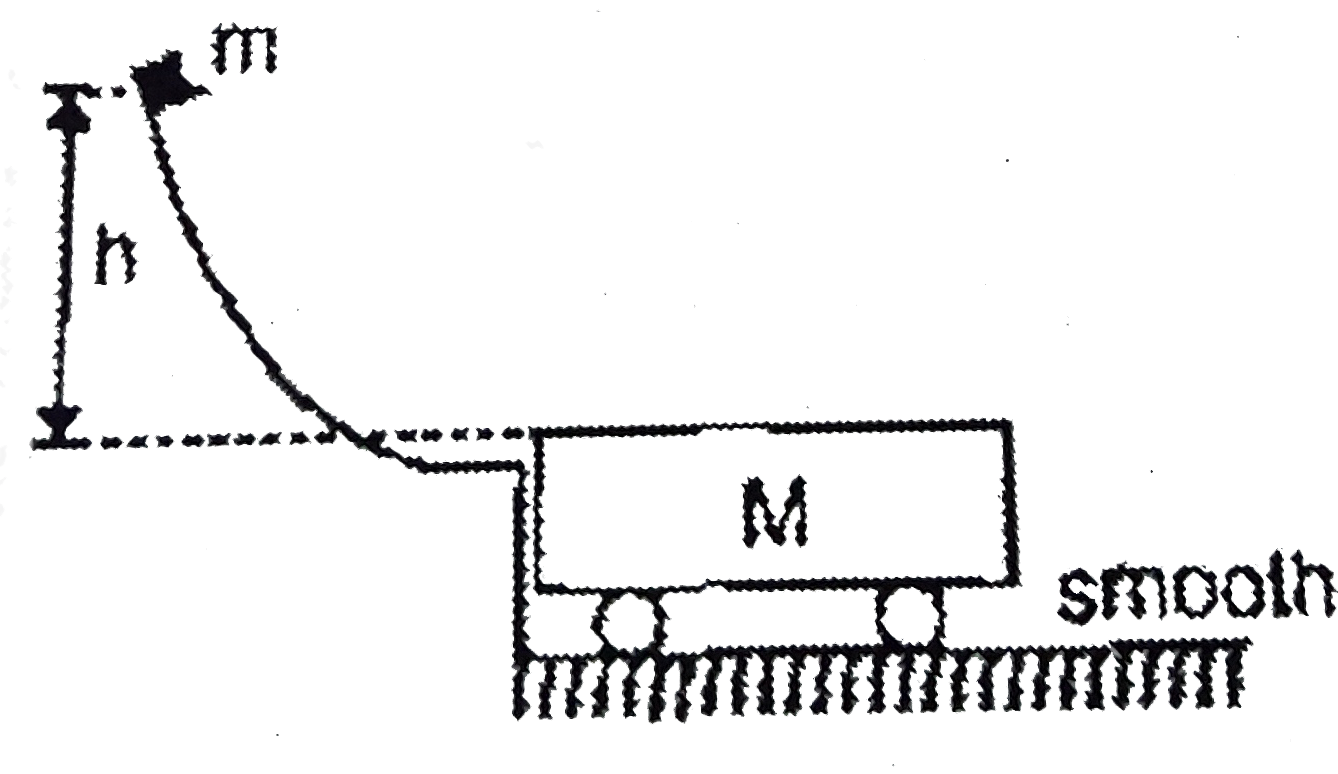
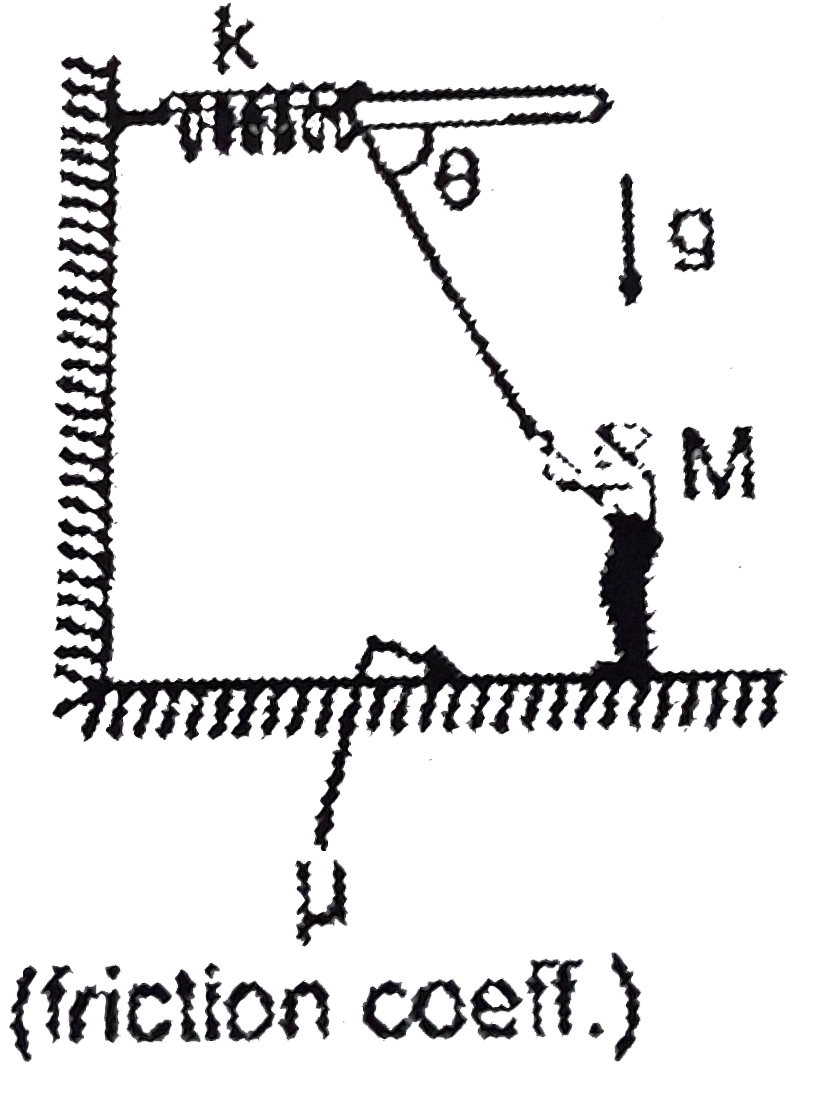
View SolutionA man with mass M has its string'.attached to one end. of a spring which can move without friction along a horizontal, overhead fixed rod. The other end of the spring is fixed to a, wall. The spring constant is k. The string is massless and inextensible and it maintains a constant angle `theta` with the, overhead rod, even when the man moves. There is friction, iwith coefficient `mu` between the man and the ground. What is, the maximum distance (in m ) that the man moving slowly can stretch the spring beyond its natural length?
View SolutionFind minimum normal force to be each hand to hold there identical books in verticle position Each books has mass `m` and the value of coefficient of friction between the books as well as between hand and the book is `mu`

View SolutionIn the Fig. 2E.86 (a) shown a constant force Fis applied on lower block just large enough to make this block sliding outi from between the upper block and the table. Determine the force F at this instant and acceleration of each block. Take `g=10 m//s^(2)`.
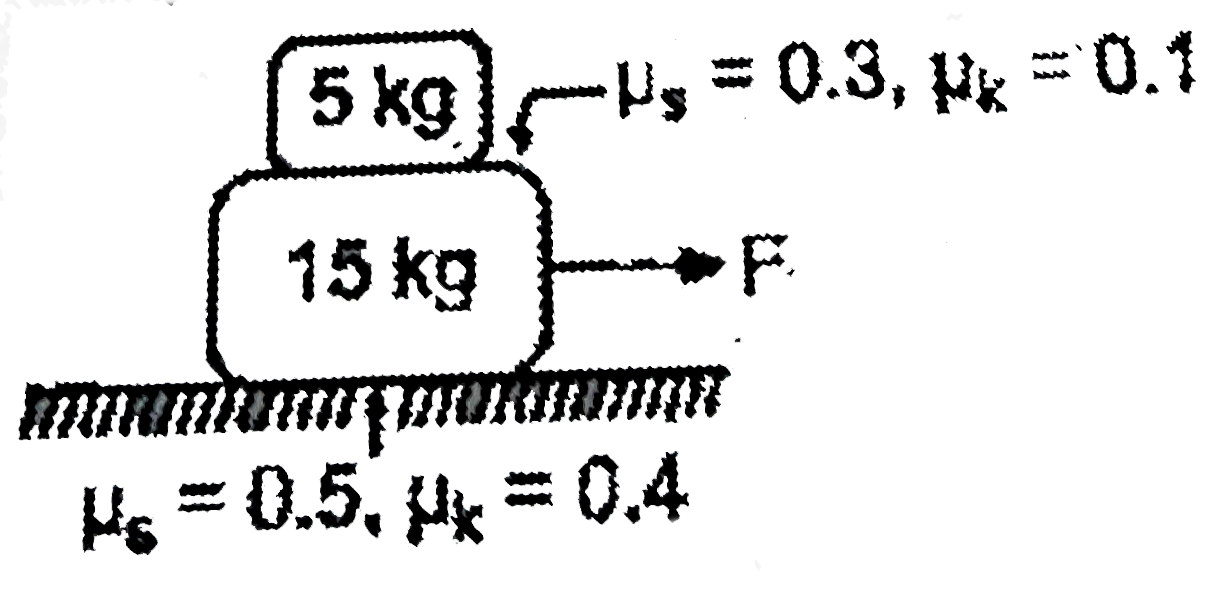
View SolutionA stone is thrown horizontally with the velocity `v_(x) = 15m//s`. Determine the normal and tangential accelerations of the stone in I second after begins to move.
View SolutionA balloon starts rising from the surface of the earth with vertical component of velocity `v_(0)`. The balloon gathers a horizontal velocity `v_(x) = ay`, where a is a constant and y is the height from the surface of the earth, due to a horizontal wind. Determine
(a) the equation of trajectory of the balloon.
(b) the tangential, normal and total acceleration of the balloon as function of y.
View SolutionA ball of mass m is suspended from a rope of length L. It describes a horizontal circle of radius r with speed v. the rope makes an angle `theta` with vertical given by `sin theta = r//2`. Determine (a) the tension in the rope and (b) the speed of the ball. (c) time period of ball.
View SolutionA car is moving along a banked road laid out as a circle of radius r . (a) What should be the banking angle `theta` so that the car travelling at speed v needs no frictional force from tyres to negotiate the turn ? (b) The coefficient of friction between tyres and road are `mu_(s) = 0.9` and `mu_(k) = 0.8` . At what maximum speed can a car enter the curve without sliding toward the top edge of the banked turn ?

View SolutionA `50 kg` woman is on a large swing (generally seen in fairs) of radius 9 m that rotates in a vertical circle at `6 "reve"//min`. What is the magnitude of her weight when she has moved halfway up ?
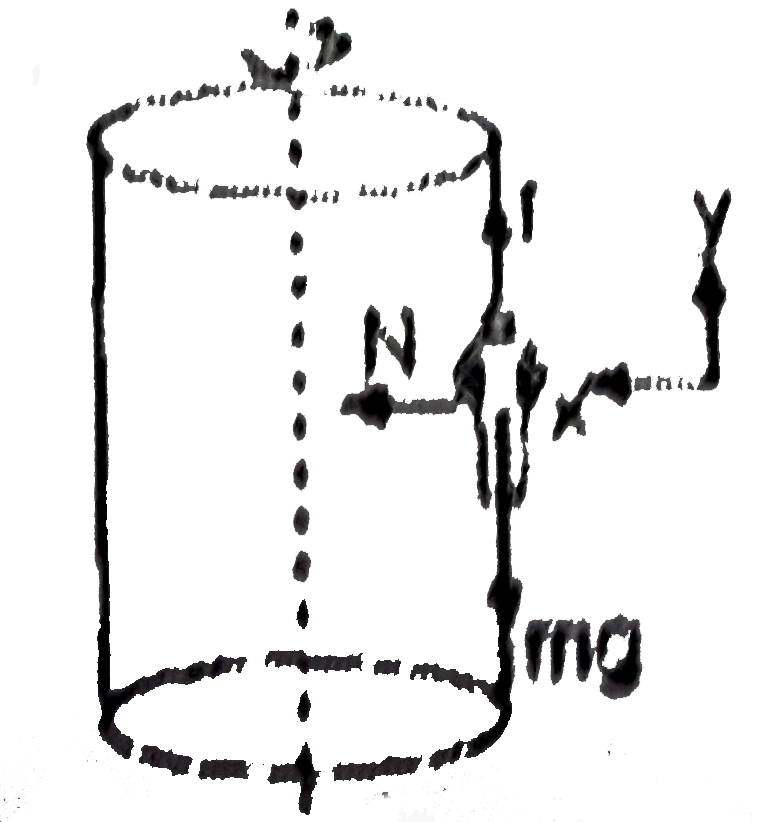
View SolutionIn amusement parks there is a device called rotor where people stand on a platform inside a large cylinder that rotates about a vertical axis. When the rotor reaches a certain angular velocity, the platform drops away. Find the minimum coefficient of friction for the people not to a slide down. Take the radius to be `2m` and the period to be `2s`.
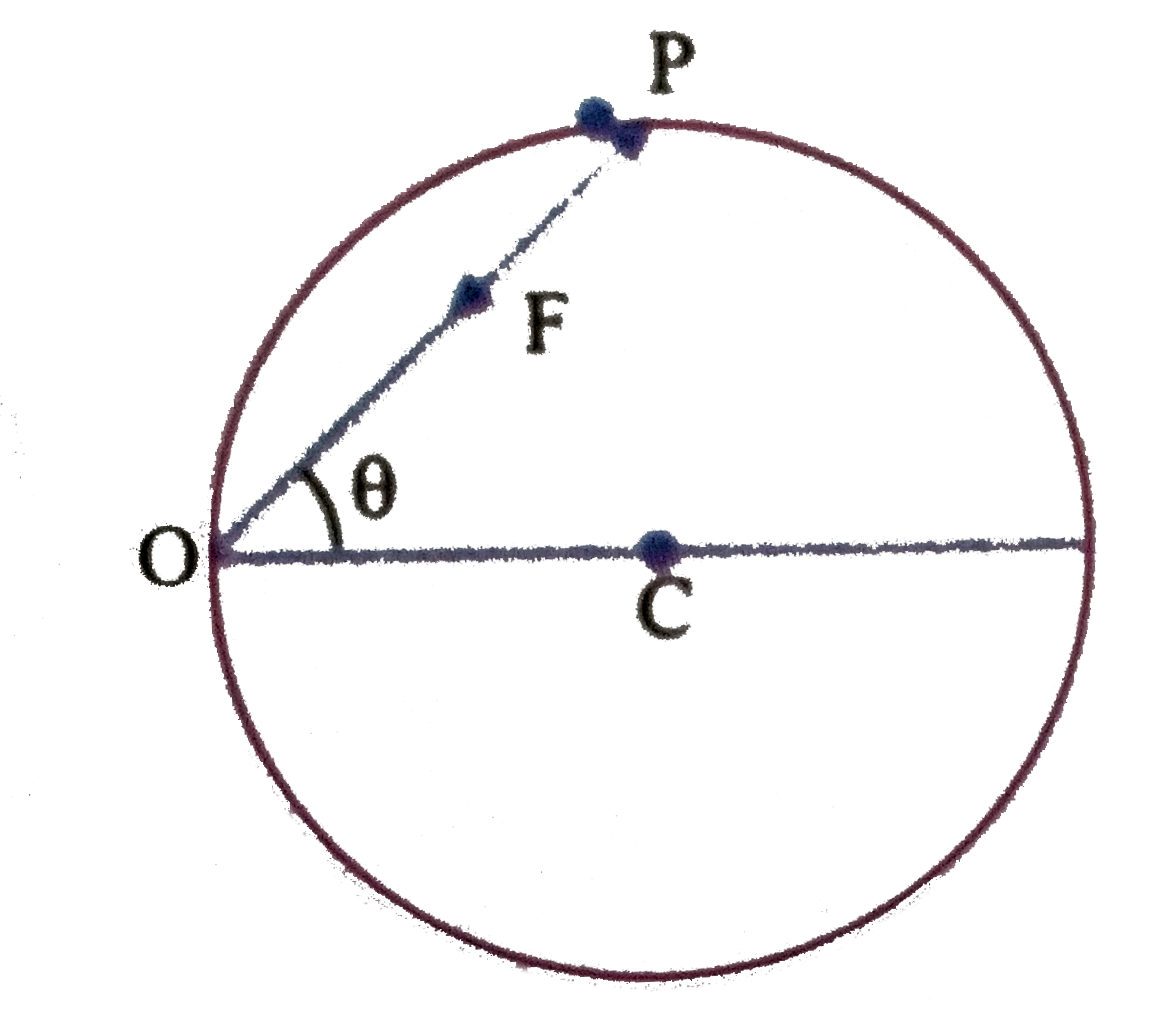
View SolutionA particle `'P'` is moving on a circular path under the action of only one force action always toward the fixed point `'O'` on the circumference. Find the ratio of `(d^(2)theta)/(dt^(2))` & `(("d"theta)/(dt))^(2)`
View SolutionA car is moving in a circular path of radius `50 m`, on a plat rough horizontal ground. The mass of the car is `1000 kg`. At a certain moment the speed of the car is `5m//s`, the driver is increasing speed at the rate of `1m//s^(2)`. Find the value of static friction on tyres at this moment, in Newtons.

View SolutionA block of mass `25 kg` rests on a horizontal floor `(mu = 0.2)`. It is attached by a `5 m` long horizontal rope to a peg fixed on floor. The block is pushed along the ground with an initial velocity of `10m//s` so that it moves in a circle around the peg. Find
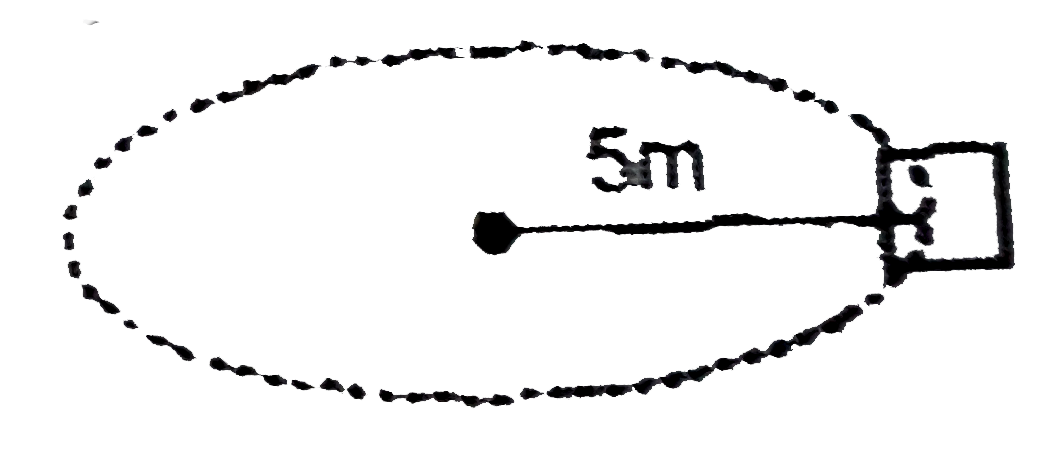
(a) Tangential acceleration of the block.
(b) Speed of the block at time t.
(c) Time when tension in rope becomes zero.
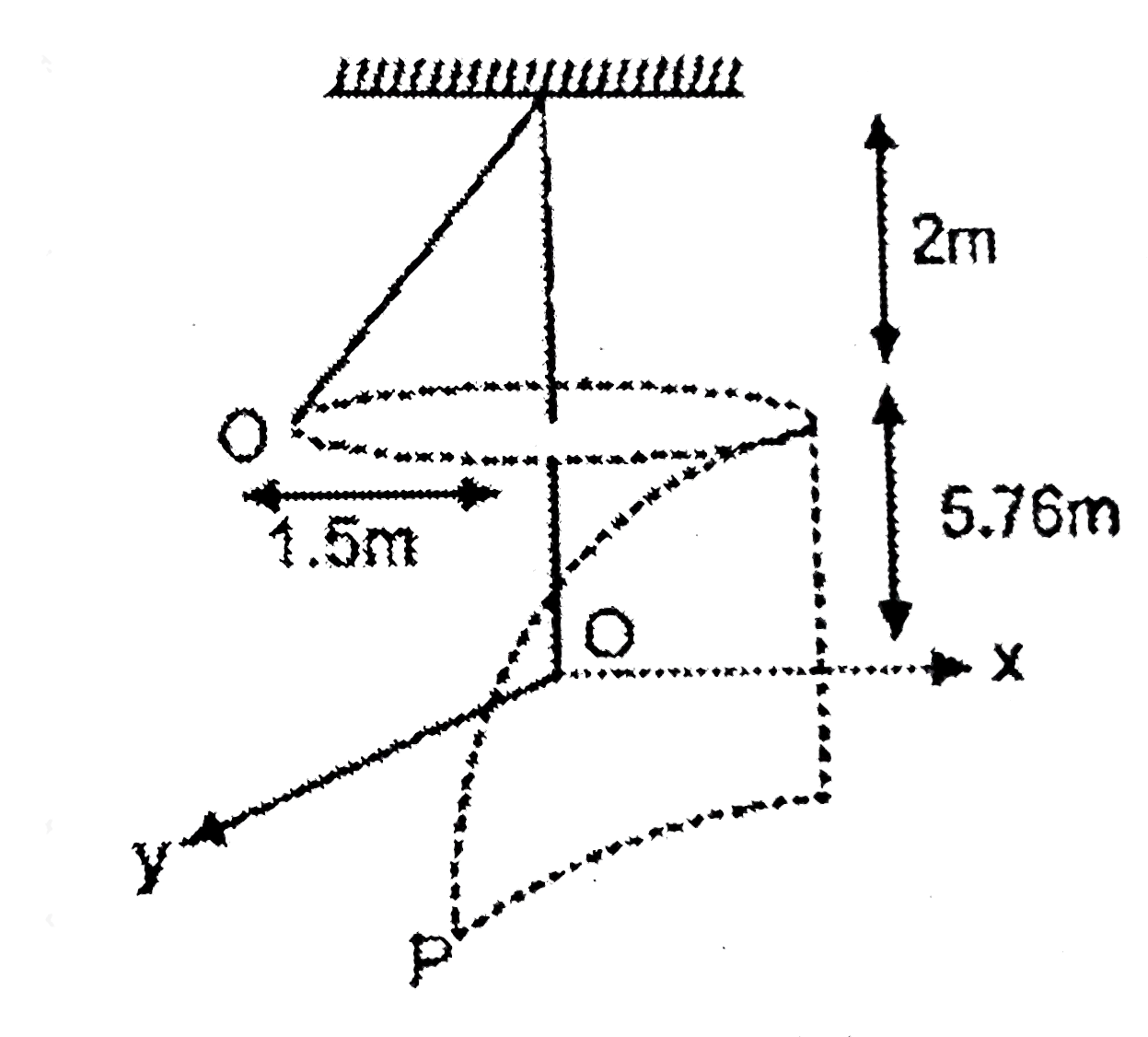
View SolutionA particle suspended from the ceiling by inextensible light string is moving along a horizontal circle of radius 1.5 m as shown. The string traces a cone of height 2 m. The string breaks and the particle finally hits the floor (which is zy plane 5.76 m below the circle) at point P. Find the distance OP.
View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance `r` from the axis the coefficient of fraction between the block and the inclined plane is `mu` The turntable along with incline plane spins about its axis with constant minimum angular velocity `omega`
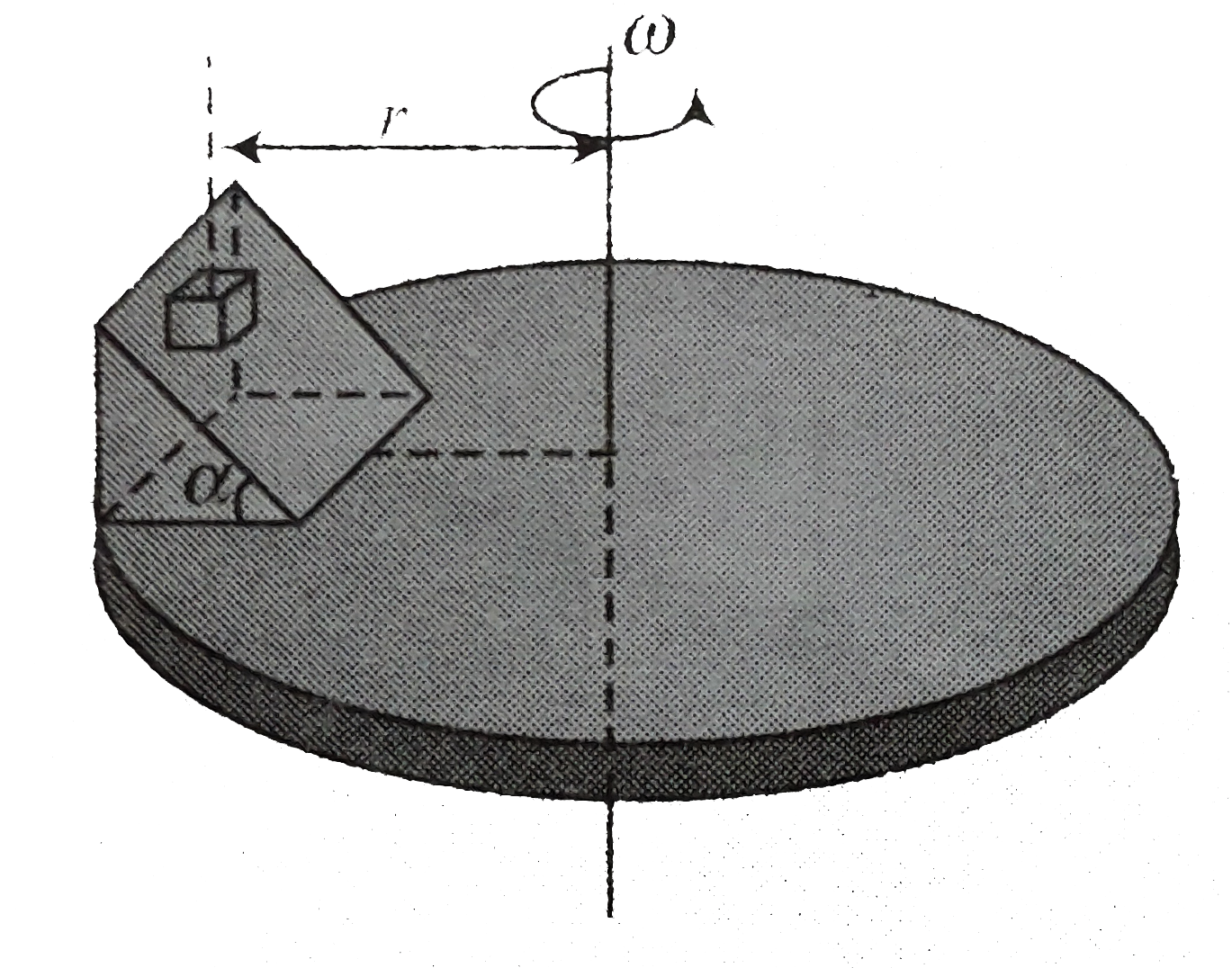
a. Find an capression for the minimum angular velocity `omega` to prevent the block from sliding down the plane in term of `g, r, mu ` and the plane `omega`
b. Now a block of mass but having coefficient friction (with inclined plane)`2mu` is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View SolutionA circular race track is banked at `45^(@)` and has a radius of 40 m. at what speed does a car have no tendency to slip? If the coefficient of friction between the wheels and the track is `1/2`, find the maximum speed at which the car can travel round the track without skidding.
View SolutionA stone is launched upward at `45^(@)` with speed `v_(0)`. A bee follow the trajectory of the stone at a constant speed equal to the initial speed of the stone.
(a) Find the radius of curvature at the top point of the trajectory.
(b) What is the acceleration of the bee at the top point of the trajectory? For the stone, neglect the air resistance.
View SolutionA rock is launched upward at `45^(@)`. A bee moves along the trajectory of the rock at a constant speed equal to the initial speed of the rock. What is the magnitude of acceleration (in `m//s^(2)`) of the bee at the top point of the trajectory? For the rock, neglect the air resistance.
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity `omega`. Inner surface of bowl is rough, coefficient of friction is `mu`. The block is kept at a position where radius makes an angle `theta` with the vertical. What is the range of the angular speed for which the block will stay at the given position?
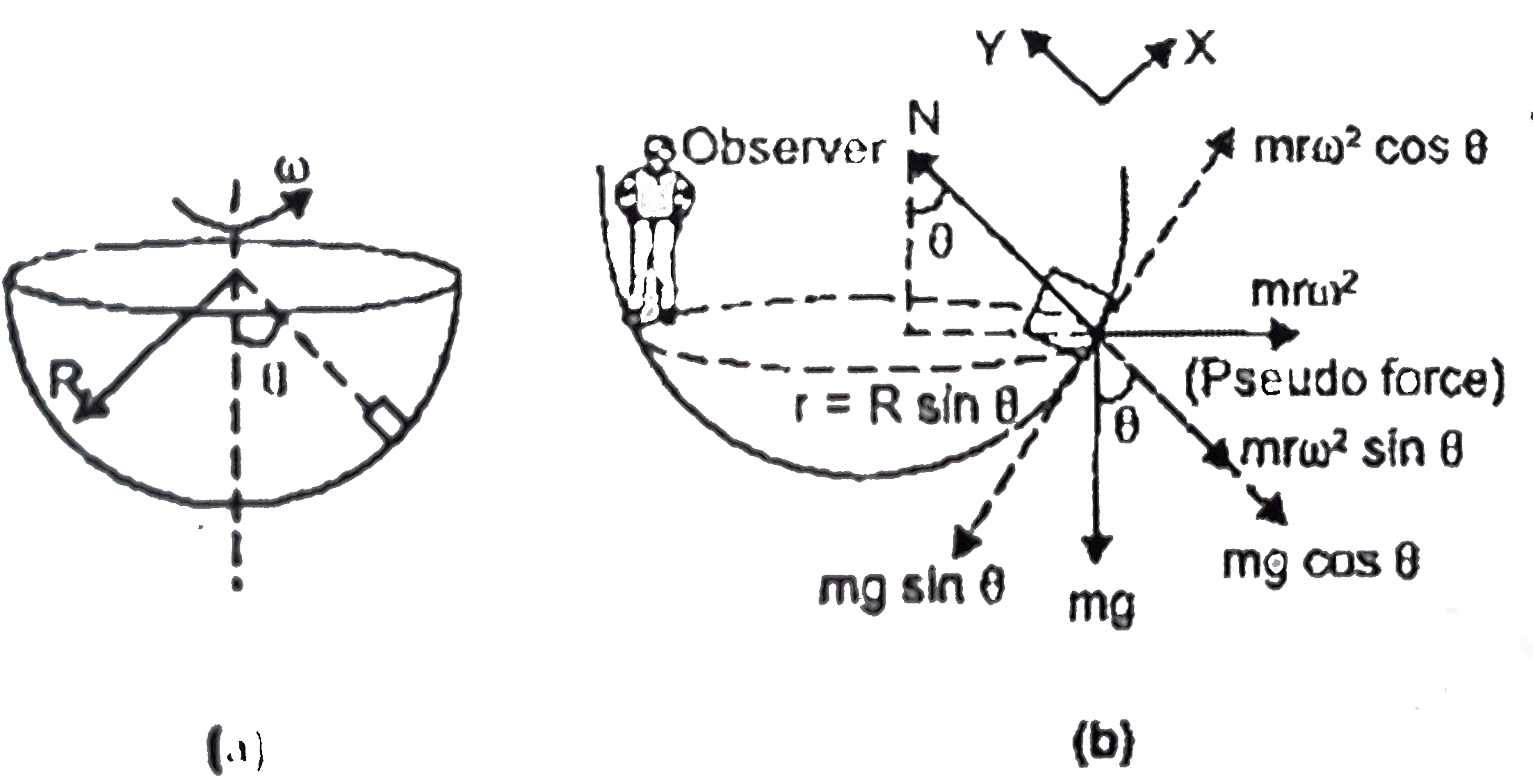
View SolutionA wedge with mass M rests on a frictionless horizontal surface A block with mass m is placed on the wedge. There is no friction between the block and the wedge. A horizontal force f is applied to the wedge. What magnitude F must have if the block is to remain at constant height above the table top?

View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length `3R//4` is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of `60^@` with the vertical. The spring constant `K=mg//R`. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

View SolutionA small bead of mass m is given an initial velocity of magnitude `v_(0)` on a horizontal circular wire. If the coefficient of kinetic friction is `mu_(k)`, determine the distance travelled before the collar comes to rest.
View SolutionIn Fig. shown two blocks are kept on a rough table, where `m_(A)=0.9 kg, m_(B)=1.7 kg, r=13 cm, mu_(s)=0.1`. Consider friction between all the contact surface, pulley is frictionless. Determine the angular speed of the turn-rable for which the blocks just begin to slide
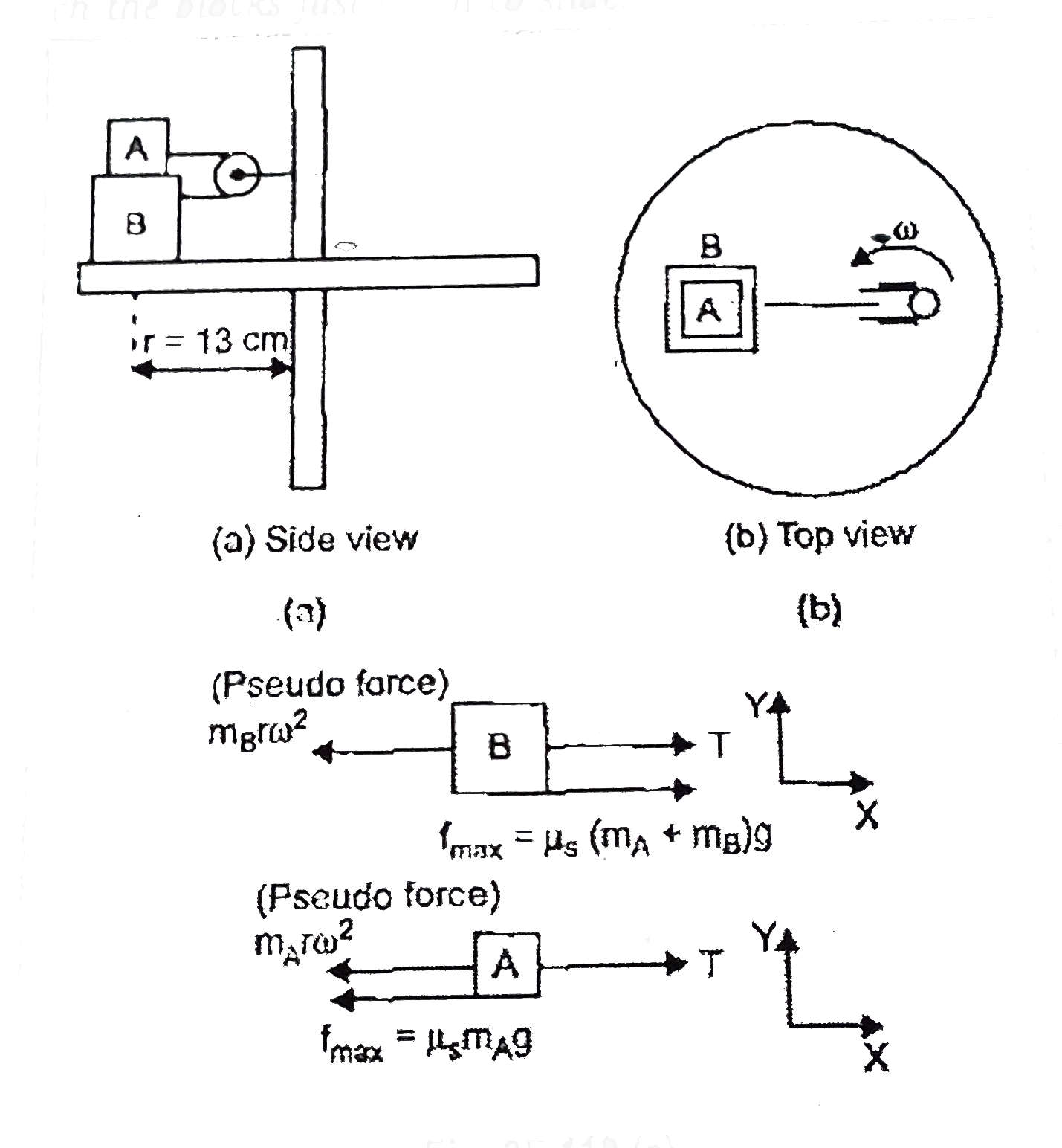
View Solution
Example questions and complete solutions for chapter FORCE ANALYSIS of SHREE BALAJI PHYSICS (HINGLISH) of Class 11