Complete Solutions to level 1 of chapter FORCE ANALYSIS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FORCE ANALYSIS |
| ANURAG MISHRA | level 1 |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A cyclist moves with uniform velocity down a rough inclined plane of inclination `alpha`. Total mass of cycle & cyclist is m. Then the magnitude and direction of force acting on the cycle from inclined plane is :
View SolutionA block of mass 5 kg is dropped from top of a building. Then the mamiitude of force applied by the block on the earth whne falling is :
View SolutionIn a vertical disc two grooves are made as shown in figure. AB is a diameter. Two balls are dropped at A one in each groove, simultaneously. Then:

View SolutionIn the given diagram, with what force must the man pull the rope to hold the plank in position? Weight of the man is 60 kg. Neglect the weight of plank, rope and pulley.
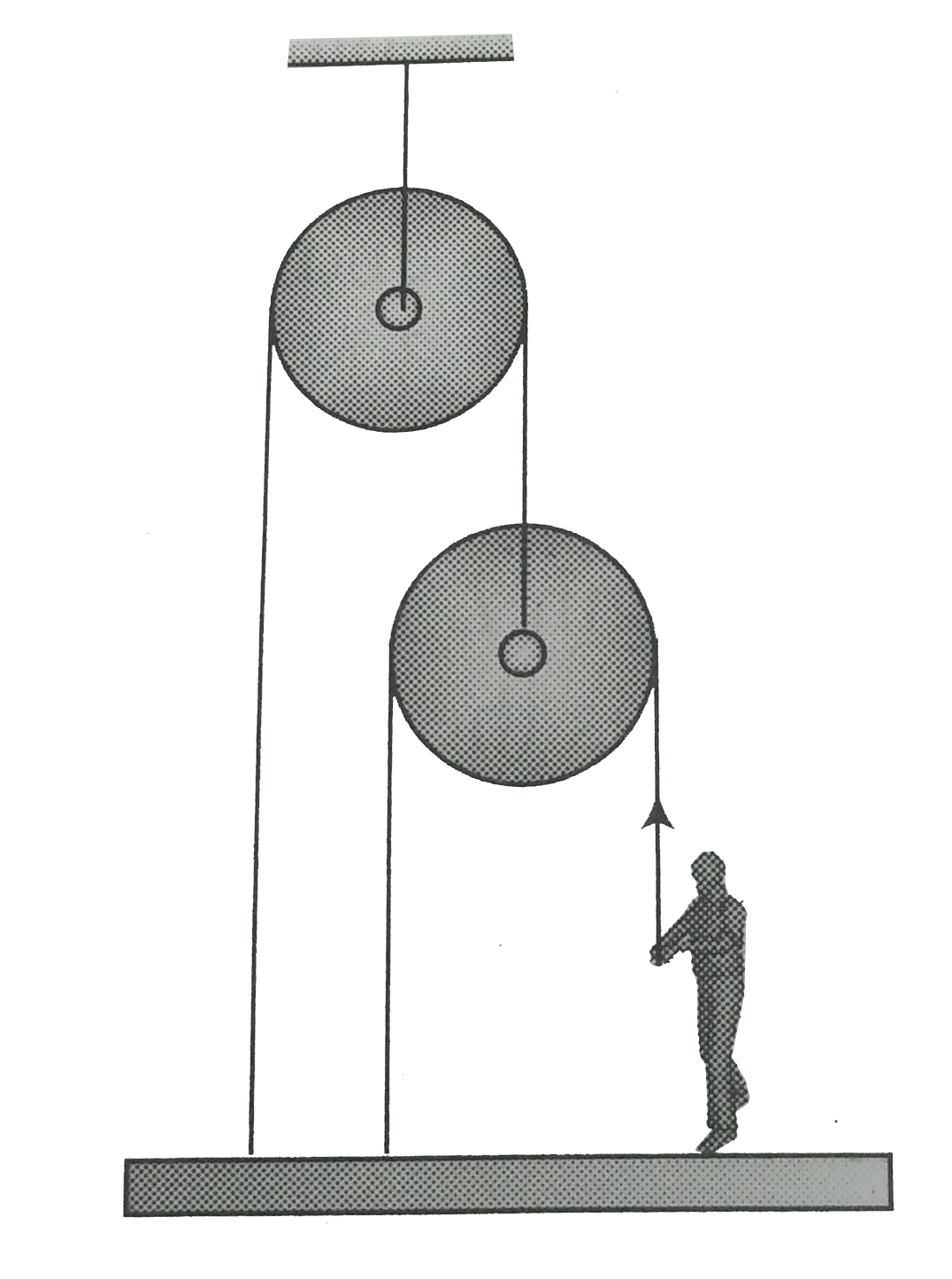
View SolutionIn the situation shown in figure the magnitude of total external force acting on the block a is (all the surfaces are smooth)

View SolutionIn the figure a rope of mass m and length `l` is such that its one end is fixed to rigid wall and the other is applied with a horizontal force F as shown below, then tension at the middle of the string is:

View SolutionThe sum of all electromagnetic force between different particles of a system of charged particles is zero :
View SolutionFigure shows a light spring balance connected to two blocks of mass 20 kg each. The graduations in the balance measure the tension in the spring. (A). What is the reading of the balance? (b).Will the reading change if the balance is heavy, say 2.0 kg? (c). What will happen if the spring is light but the blocks the unequal masses?

View SolutionA block of mass 10 kg is suspended through two light spring balance as shown below:

View SolutionA force `F_1` acts on a particle so as to accelerate it from rest to a velocity v. The force `F_1` is then replaced by `F_2` which decelerates it to rest
View SolutionTwo objects A and B are thrown upward simultaneously with the same speed. The mass of A is greater than the mass of B. Suppose their exerts a constant and equal force of resistance on the two bodies.
View SolutionA smooth wedge A is fitted in a chamber hanging from a fixed ceiling near the earth's surface.A block B placed at the top of the wedge takes a time T to slide down the length of the wedge. If the block is placed at the top of the wedge and the cable supporting the chamber is broken at the same instant, the block will
View SolutionIn an imaginary atmosphere, the air exerts a small force F on any particle in the direction of the particle's motion. A particle of mass m projected upward takes time `t_1` and reaching the maximum height and `t_2` in the return journey to the original point. Then
View SolutionA person standing oin the floor of an elevator drops as coin. The coin reaches the floor of the elevator in a time `t_1` if the elevator is stationary and in the `t_2` if it is moving uniformly. Then
View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View Solution
An ideal spring is compressed and placed horizontally between a vertical fixed wall and a block free to slide over a smooth horizontal table to as shown in the figure. The system is released from rest. The graph which represents the relation between the magnitude of acceleration `a` of the block and the distance `x` travelled by it (as long as the spring is compressed) is
View SolutionA steel ball is placed on the surface of water in a deep tank. Water exerts a resistive force which is proportional to the velocity of the ball. The steel sinks into the water:
View SolutionIn the arrangement shown below pulleys are mass less and frictionless and threads are in responsible block of mass `m_(1)` will remain at rest if :

View SolutionA fireman want to slide down a rope. The breaking load the rope is `3//4^(th)` of the weight of the man. With what minimum acceleration should the fireman slide down ?
View SolutionAn empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
View SolutionA metal sphere is hung by a string fixed to a wall. The forces acting on the sphere are shown in figure. Which of the following statement is/are wrong ?

View SolutionA force `vecF=vecvxxvecA` is exerted on a particle in addition to the force of gravity, where `vecv` is the veocity of the particle and `vecA` is a constant vector in the horizontal direction. With what minimum speed a particle of mass m be projected so that it continues to move undeflected with a constant velocity?
View SolutionA particle of small m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force on the pulley is
View SolutionBlock A and C starts from rest and move to the right with acceleration `a_(A)=12tms^(-2)` and `a_(C )=3ms^(-2)`. Here t is in second. The time when block B again comes to rest is

View SolutionIn order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration `5g//4` relative to the rope. The tension in the rope is (take `g=10 ms^(-2)`)

View SolutionA ball is held at rest in position A by two light cords. The horizontal cord is now cut and the ball swings to the position B. What is the ratio of the tension in the cord in position B to that in position A?
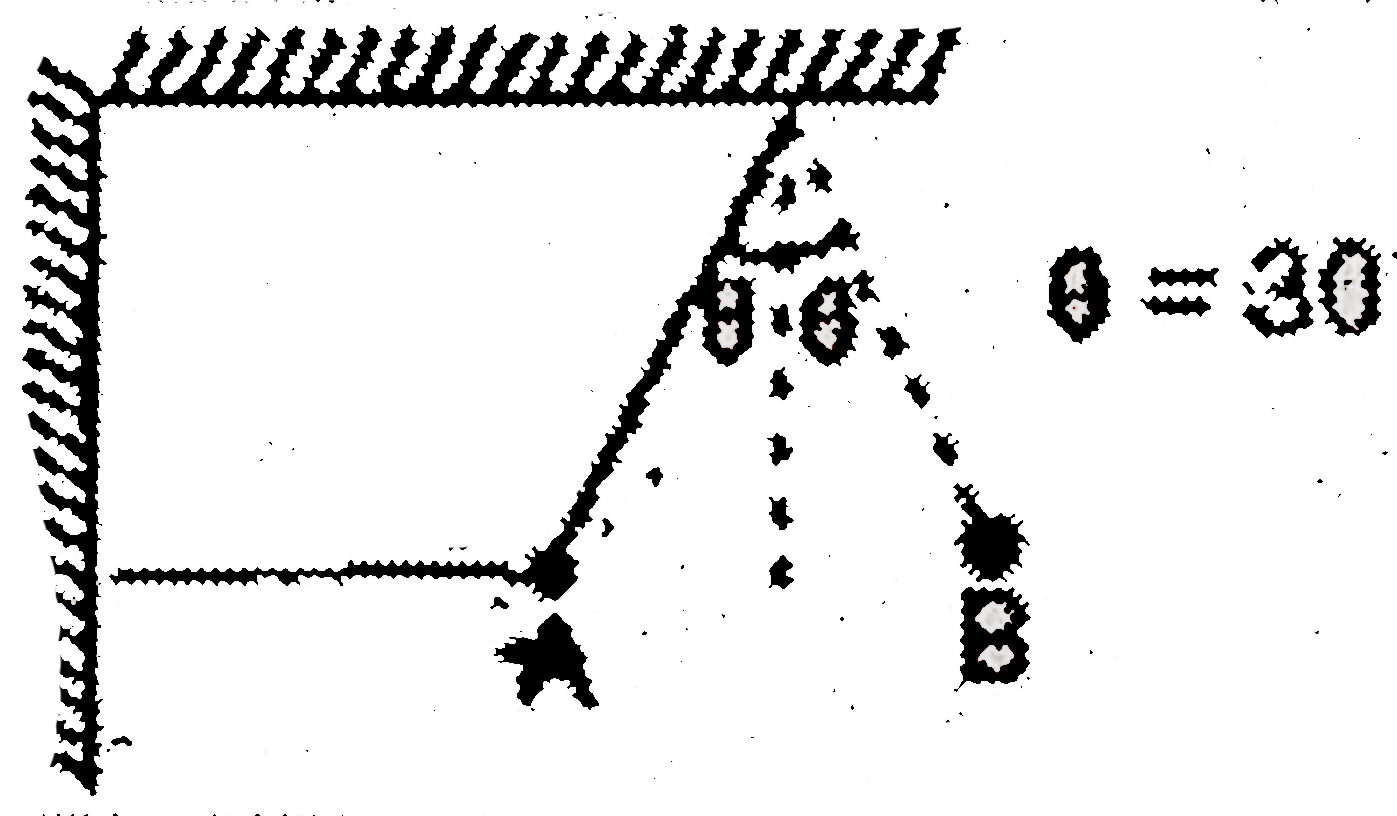
View SolutionIn the shown figure two beads slide along a smooth horizontal rod as shown in figure. The relation between v and `v_(0)` in the shown position will be

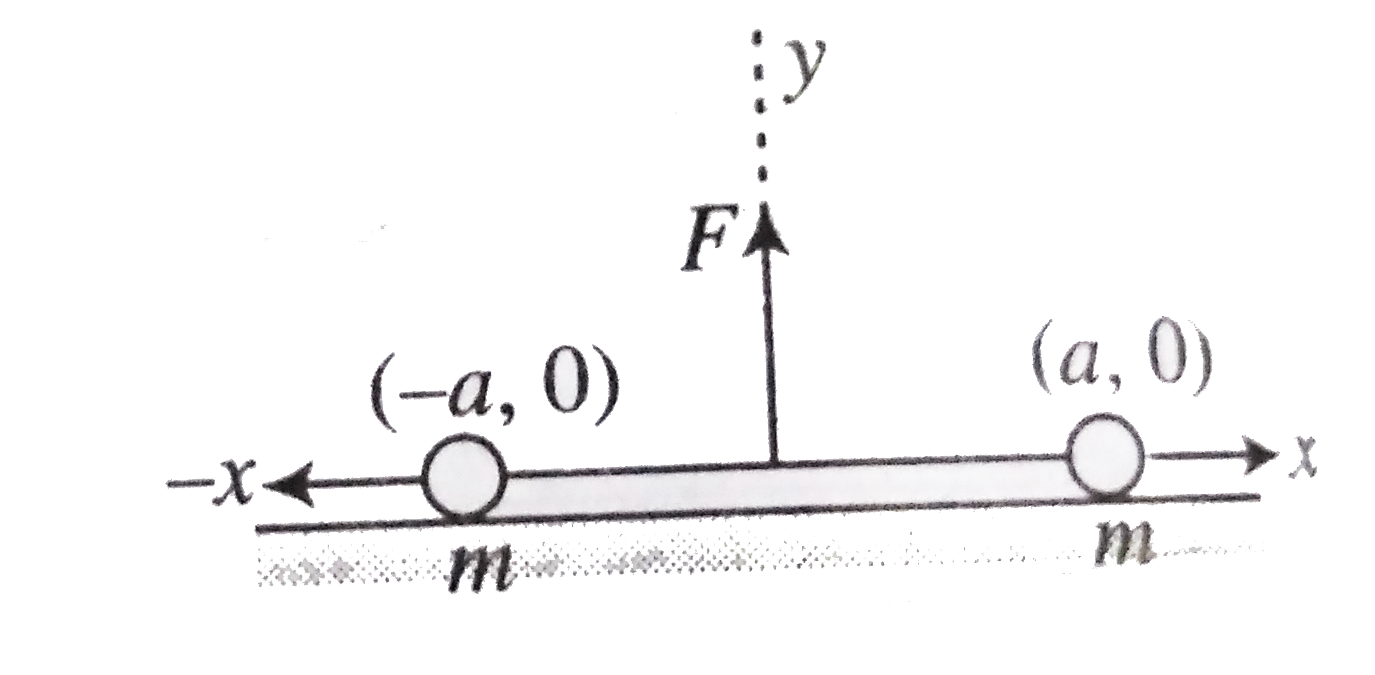
View SolutionTwo masses each equal to m are lying on x-axis at `(-a,0)(+a,0)` respectively as shown in figure They are connected by a light string A force F is applied at the origin along vertical direction As a result the masses move toward each other without loosing contact with ground What is the acceleration of each mass? Assume the instantanceous position of the masses as`(-x,0)`and `(x,0)`
View SolutionAll surfaces shown in figure are smooth. System is released with the spring instretched. In equilibrium, compression in the spring will be

View SolutionFind the maximum compression in the spring, if the lower block is shifted to rightwards with acceleration 'a'. All the surfaces are smooth :

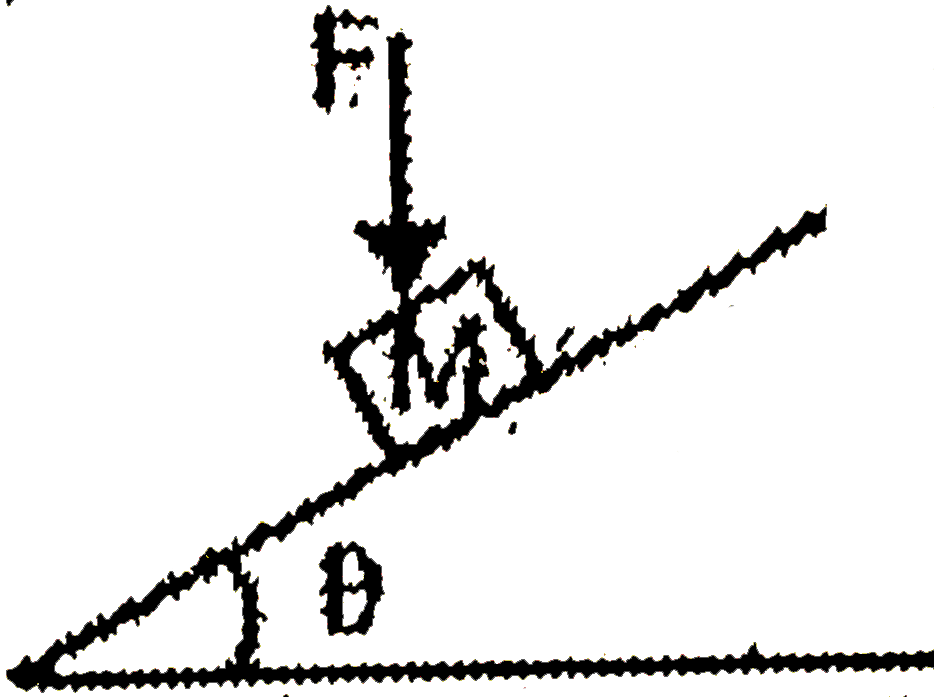
View SolutionA block of mass M is sliding down the plane. Coefficient of static friction is `mu_(s)` and kinetic friction is `mu_(k)`. Then friction force acting on the block is :
View SolutionThe displacement time curve of a particle is shown in the figure. The external force acting on the particle is :
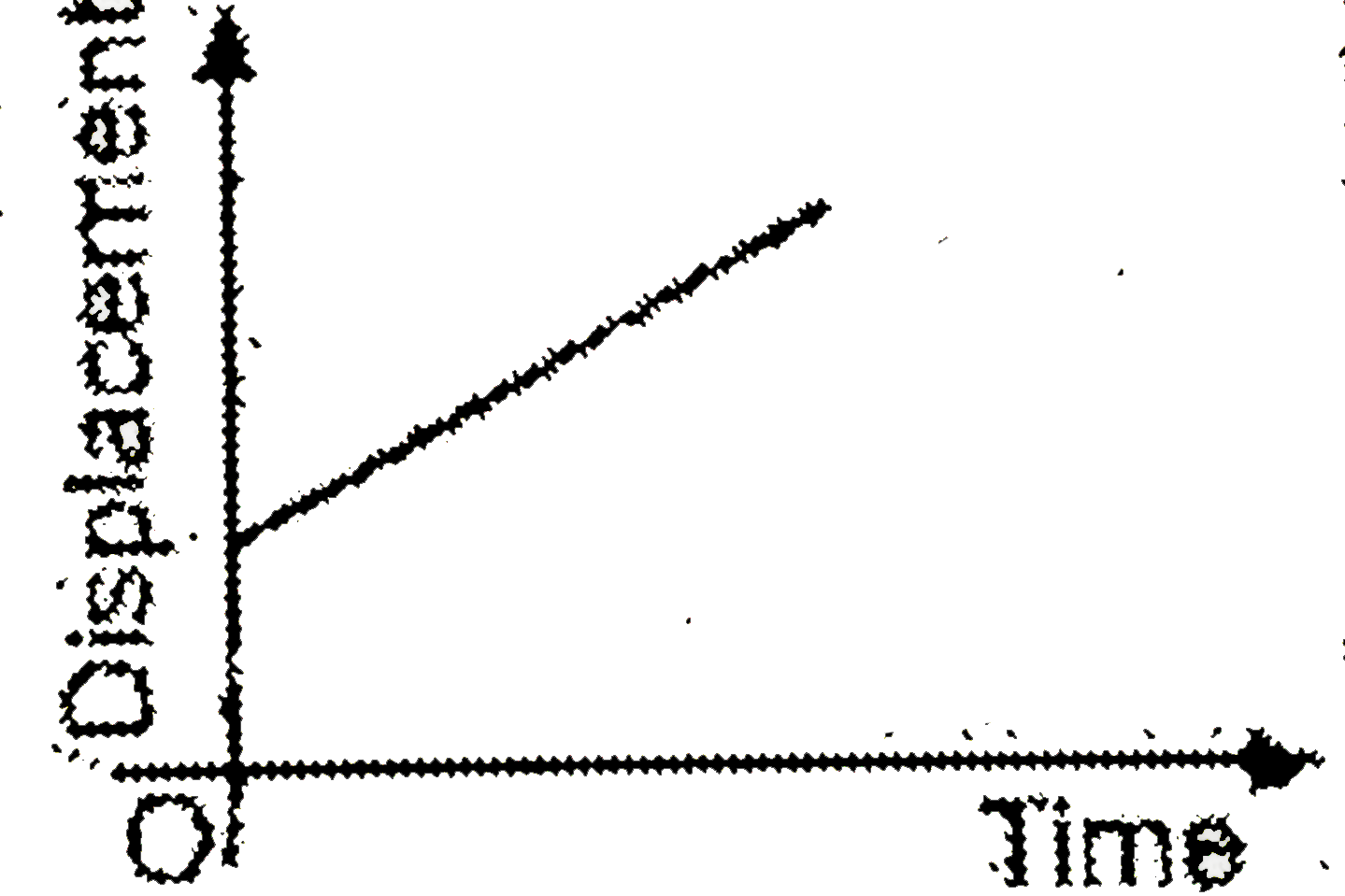
View SolutionA block of mass 'M' is slipping down on a rough inclined of inclination `alpha` with horizontal with a constant velocity. The magnitude and direction of total reaction from the inclined plane on the block is :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA body of mass M is kept n a rough horizontal surfasce (friction coefficient `=mu`). A person is trying to pull he body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
View SolutionA spring of force constant k is cut inot two places such that one piece is double the length of the other. Then the long piece will have a force-constant of :
View SolutionIn the arrangement shown in figure the wall is smooth and friction coefficient between the blocks is `mu = 0.1`. A horizontal force `F = 1000 N` is applied on the `2kg` block. The wrong statement is :

View SolutionTwo blocks are kept on an inclined plane and tied to each other with a mass-less string. Coefficient of friction between `m_(1)` and inclined plane is `mu_(1)` & that betweeb `m_(2)` & the inclined is `mu_(2)`. Then :
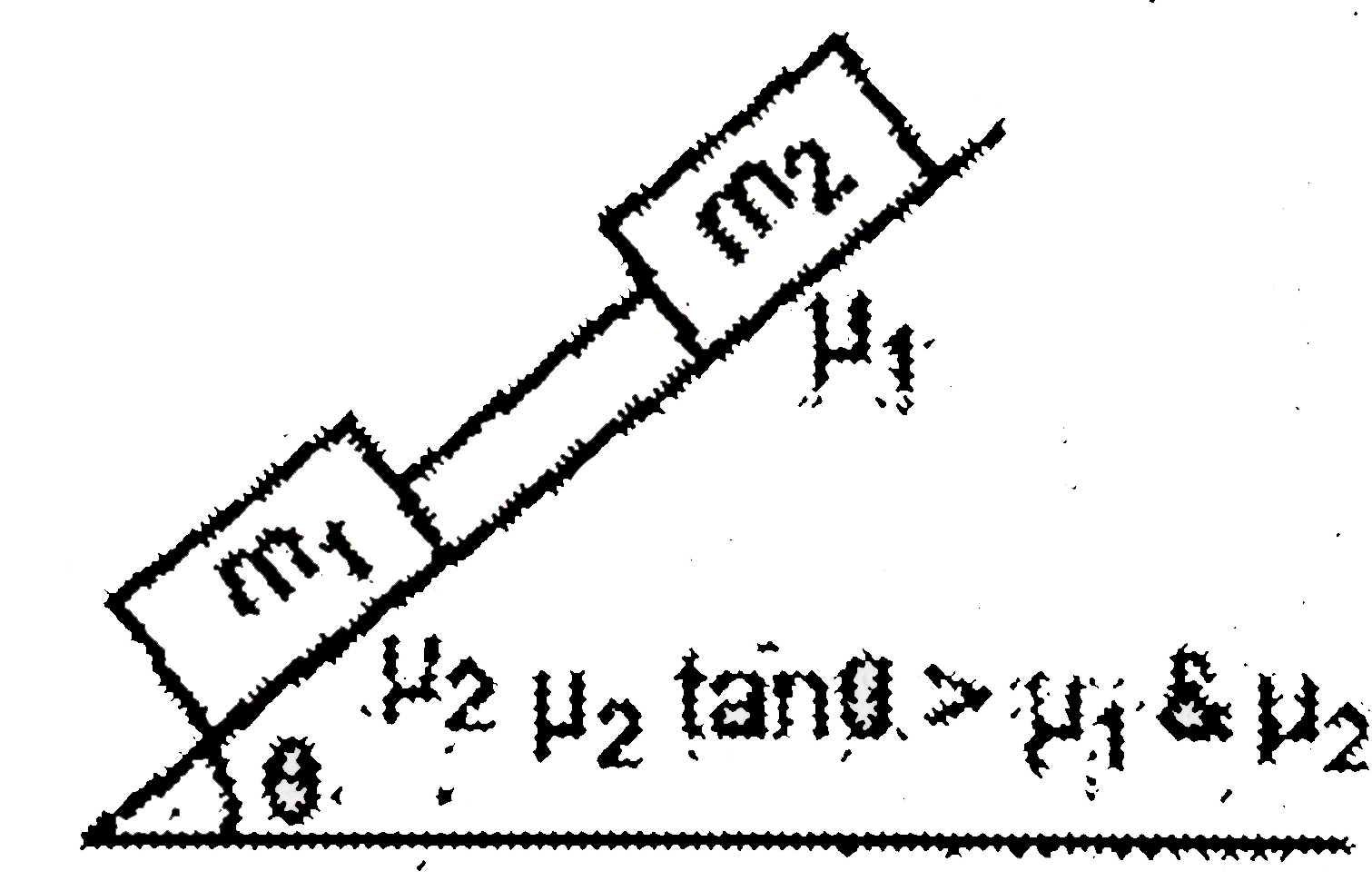
View SolutionA block kept on an inclined surface, just begins to slide if the inclination is `30^(@)`. The block is replaced by another block B and it is just begins to slide if the inclination is `40^(@)`, then :
View SolutionA force of `100 N` is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is `1//4`. The friction force acting on the block is :
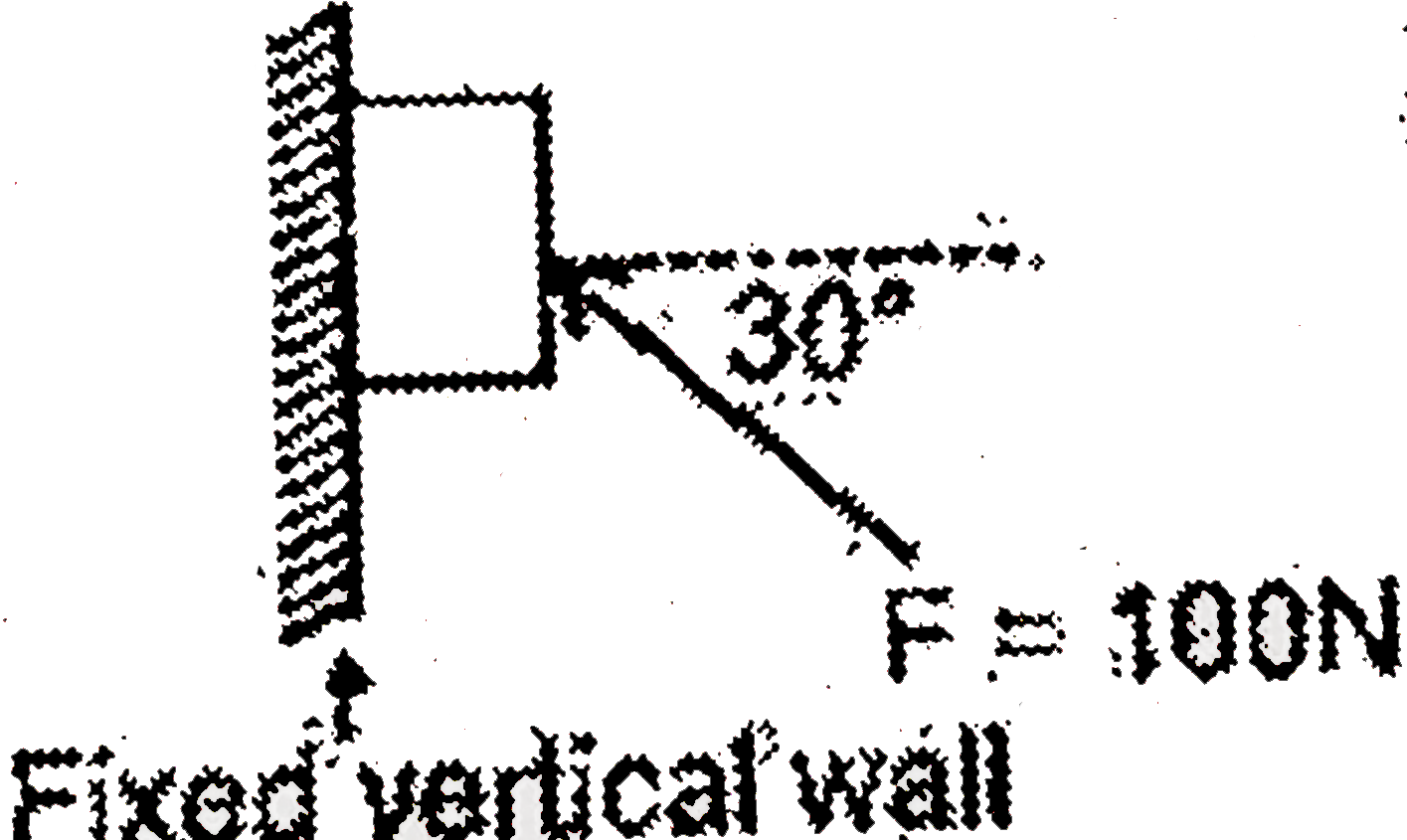
View SolutionAn insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle `alpha` with the vertical, the maximum possible value of `alpha` is given by
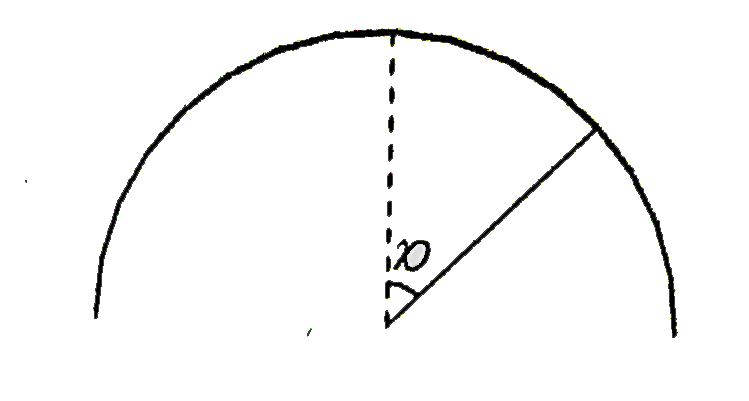
View SolutionA block of mass 2kg is held at rest against a rough vertical wall by passing a horizontal (normal) force of `45 N`. Coefficient of friction between wall and the block is equal to 0.5. Now a horizontal force of `15 N` (tangential to wall) is also applied on the block. Then the block will :
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

View SolutionThe pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle `theta` should be :

View SolutionThe force `F_(1)` required to just moving a body up an inclined plane is double the force `F_(2)` required to just prevent the body from sliding down the plane. The coefficient of friction is `mu`. The inclination `theta` of the plane is :
View SolutionA stationary body of msas m is slowly lowered onto a rough massive platform moving at a constant velocity `v_(0) = 4m//s`. The distance the body will slide with respect to the platform `mu = 0.2 ` is :

View SolutionIn the diagram shown the ground is amooth and `F_(1)` & `F_(2)` are both horizontal forces. The mass of the upper block is 10 kg while that of lower block is `15 kg`. The correct statement is :

View SolutionConsider the system as shown. The wall is smooth, but the surface of block A & B in contact is rough. The friction force on B due to A equilibrium is :

View SolutionGiven `m_(A) = 30 kg, m_(B) = 10 kg, m_(C) = 20 kg`. Between a & B `mu_(1) = 0.3`, between B & C `mu_(2) = 0.2` & between C & ground `mu_(3) = 0.1`. The least horizontal force F to start motion of ant part of the system of three blocks resting upon one another as shown below is :
(Take `g = 10m//s^(2)`)
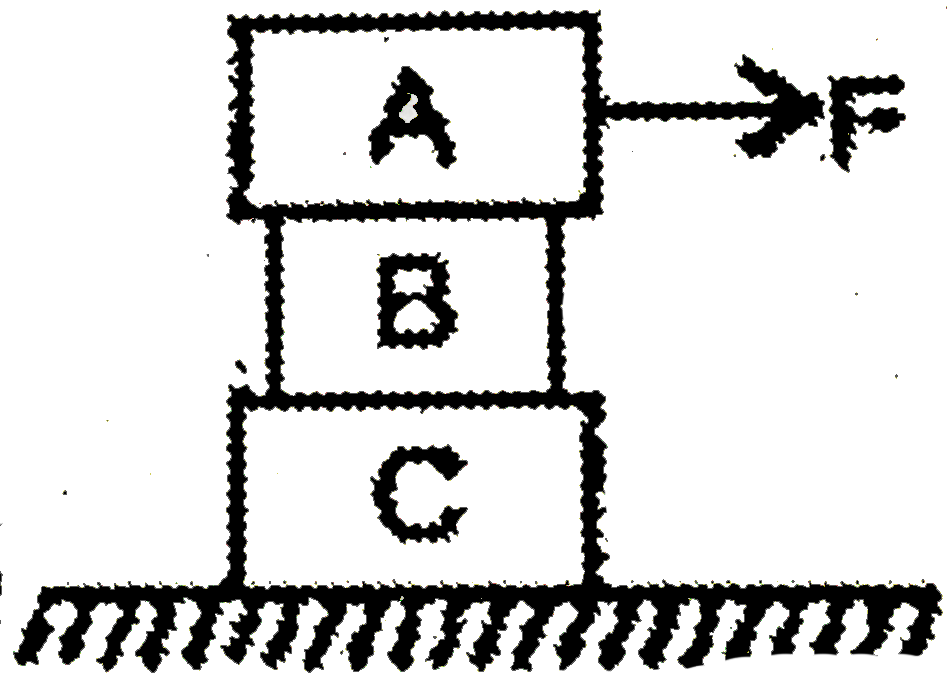
View SolutionThe coefficient of friction between the block A of mass m & block B of mass `2m` is `mu`. There is no friction between block B & the inclined plane. If the system of blocks A & B is released from rest & there is no slipping between A & B then :
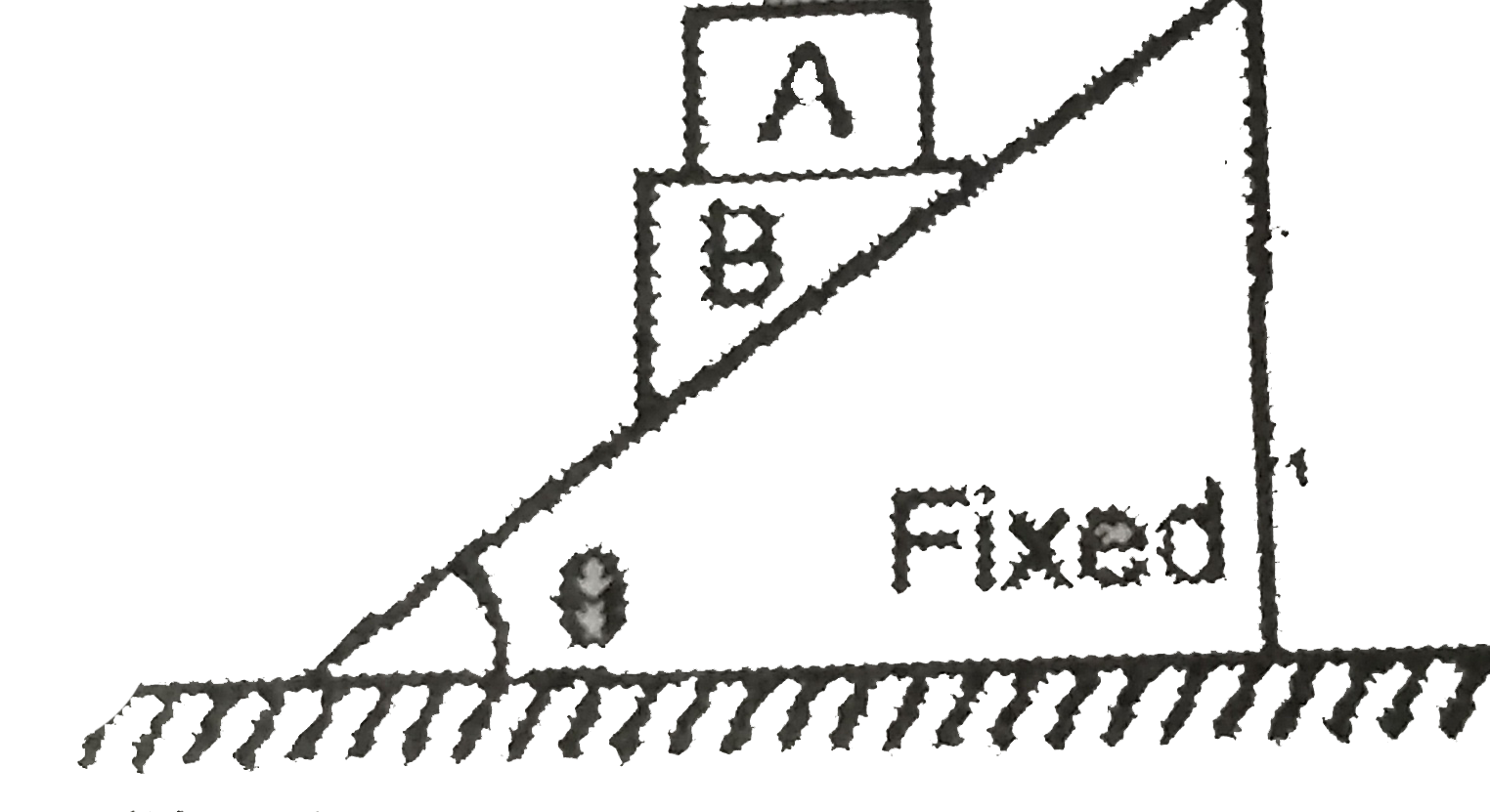
View SolutionA system is pushed by a force `F` as shown in figure All surfaces are smooth except between `B` and `C` is `mu`. Minimum value fo `F` to prevent block `B` from down ward slipping is

View SolutionA block A is placed over a long rough plank B same mass as shown below. The plank is placed over a smooth horizontal surface. At time `t = 0`, block A is given a velocity `v_(0)` in horizontal direction. Let `v_(1)` and `v_(2)` be the velocity of A & B at time 't'. Then choose the correct graph between `v_(1)` or `v_(2)` and t.
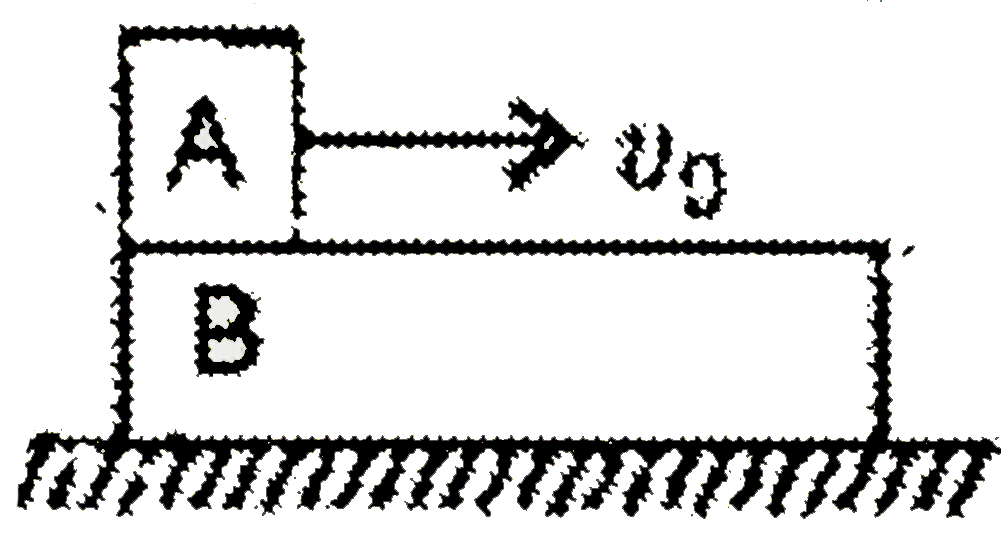
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move question:

View SolutionTwo beads A & B of equal mass m are connected by a light inextensible to move on a connected to move on a frictionless ring in vertical plane. The beads are released from rest as shown. The tension in the cord just after the release is:

View SolutionA bead of mass 'm' is attached to one end of a spring of natural length R & spring constant `k = ((sqrt3 + 1))/(R)`. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is

View SolutionIn the above question 55 tangential acceleration of the bead just after it is released is ?
View SolutionIf you want to pile up sand onto a circular area of radius R. The greatest height of the sand pile that can be created without spilling the sand onto the surrounding. Area, if `mu` is the coefficient of friction between sand particle is:
View SolutionA mass of mass `60 kg` is pulling a mass `M` by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is `mu = 1//2` find the maximum value of `M` that can be pulled on the ground

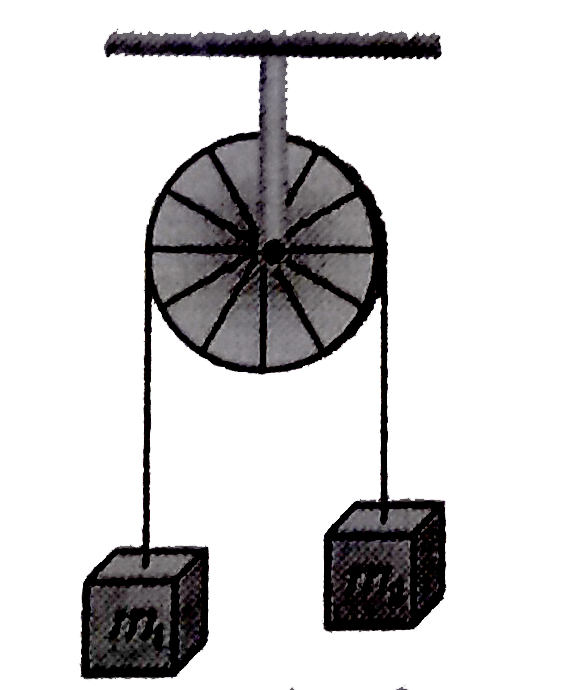
View SolutionTwo masses `m_(1)` and `m_(2)` are attached to a string which passes over a frictionless smooth pulley. When `m_(1)=10kg,m_(2)=6kg`, the acceleration of masses is
View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m walks down the board. If the coefficient of friction between the board and inclined plane is `mu = 0.5`, the minimum acceleration of does not slide is:

View SolutionA small block slides without friction down an iclined plane starting form rest. Let `S_(n)` be the distance traveled from time `t = n - 1` to `t = n`. Then `(S_(n))/(S_(n + 1))` is:
View SolutionA wedge of mass 2m and a cube of mass m are shown in figure. Between cube and wedge, there is no friction. The minimum coefficient of friction between wedge and ground so that wedge does not move is
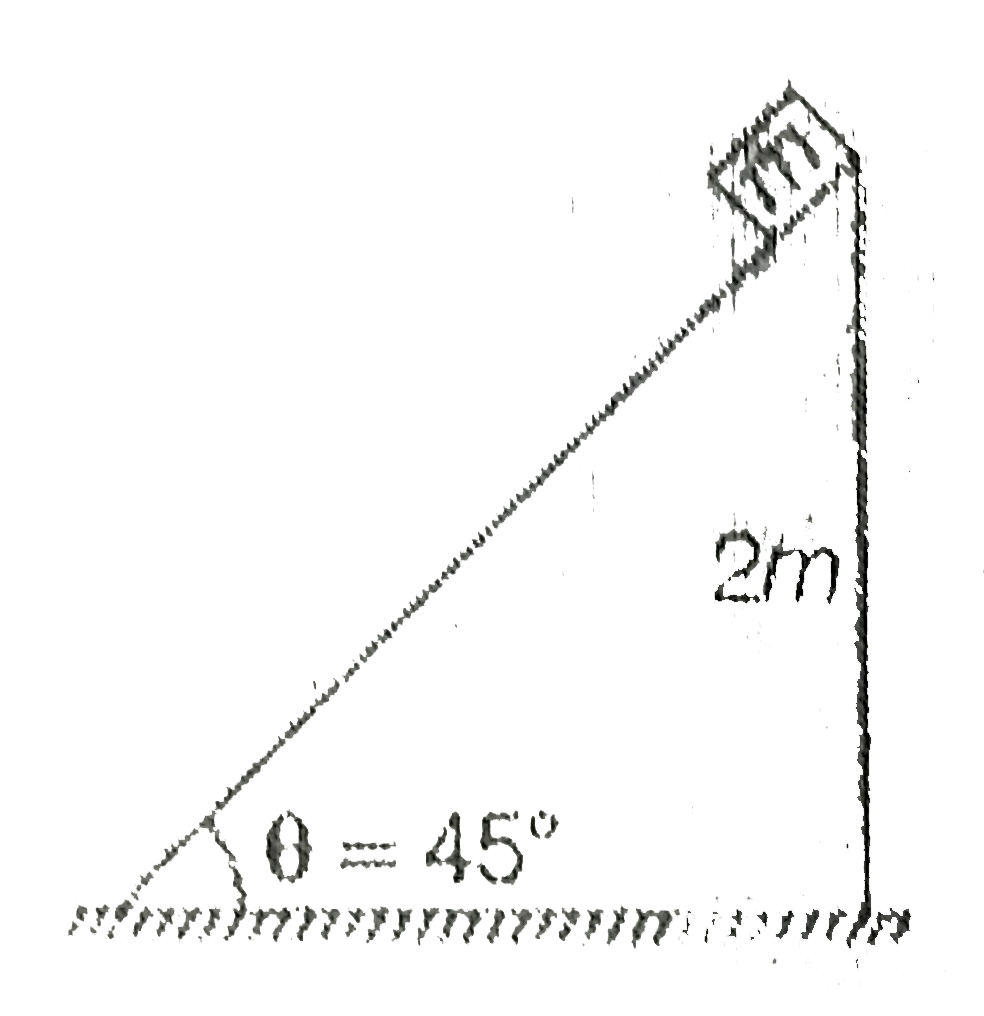
View SolutionThe figure shows a block 'A' resting on a rough horizontal surface with `mu = 0.2`. A man of mass 50 kg standing on the ground surface starts climbing the hanging ideal string. The maximum possible tension in the string is 1000N. The minimum time taken by the man to reach upto the pulley:
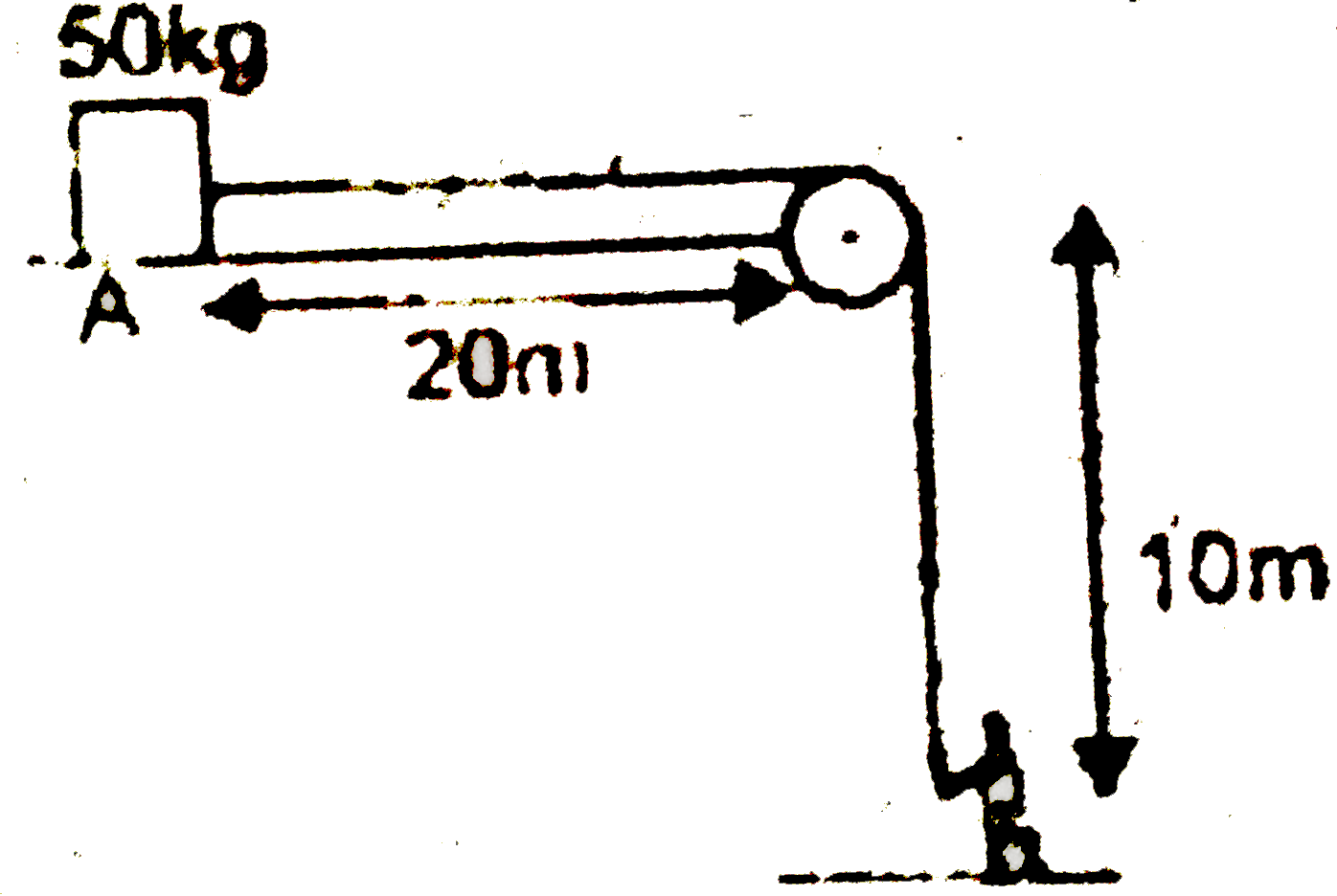
View SolutionIn the above question 63 distance between the man and the block 'A', when man reaches the pulley is:
View SolutionThe force acting on the block is given by `F = 5 - 2t`. The frictional force acting on the block after time `t = 2` seconds will be: `( mu = 0.2)`
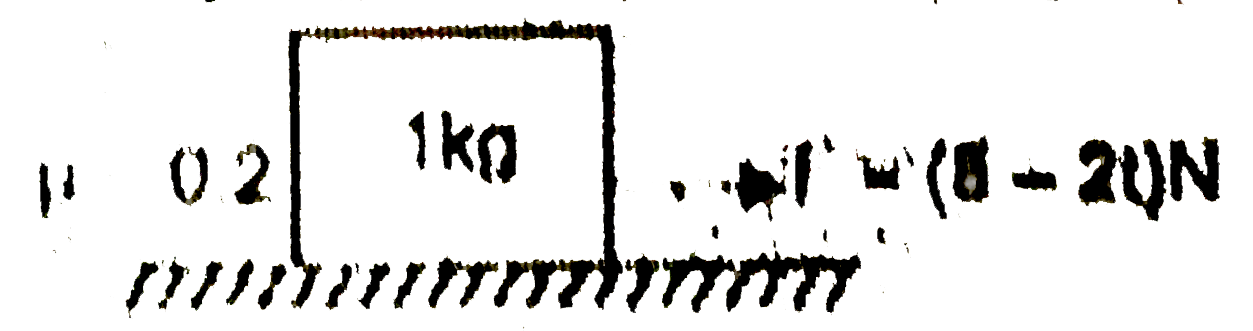
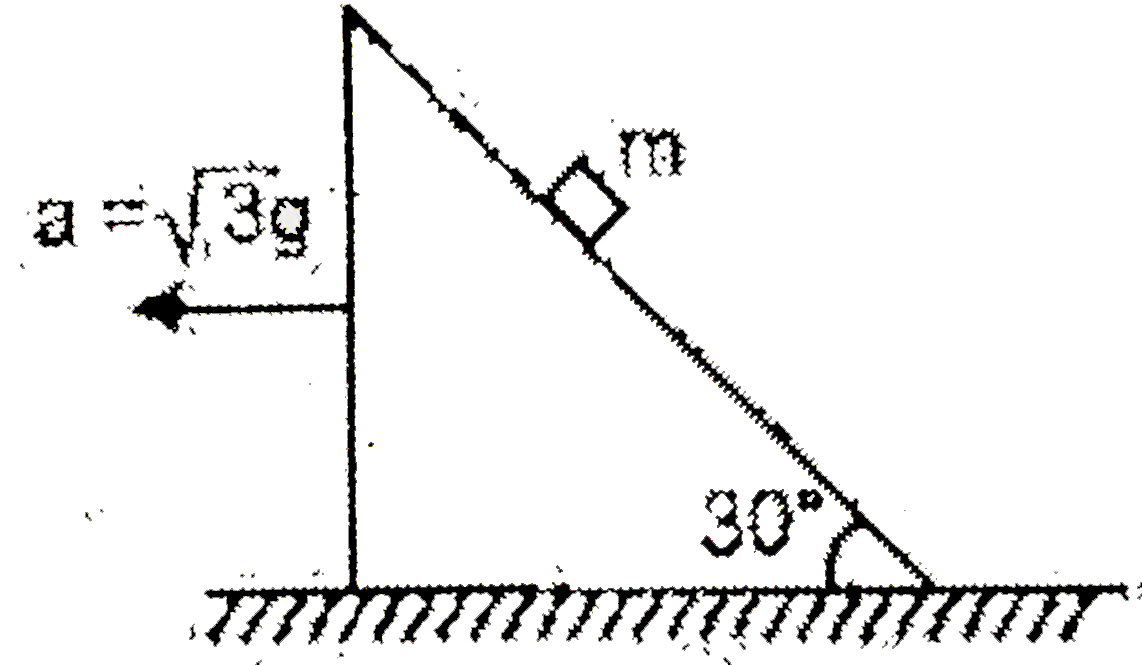
View SolutionThe acceleration of small block m with respect to ground is (all the surface are smooth):
View SolutionIn the above question 66, if the same acceleration is twoards right the frictinal force exerted by wedge on the block will be: (Coefficient of friction between wedge & block `= sqrt3//2`)
View SolutionA block of mass 'm' is held stationary against a rough wall by applying a force F as shown. Which one of the following statement is incorrect ?

View SolutionTwo blocks A and B of masses 2m and m, respectively, are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the fig The magnitudes of acceleration of A and B immediately after the string is cut, are respectively:
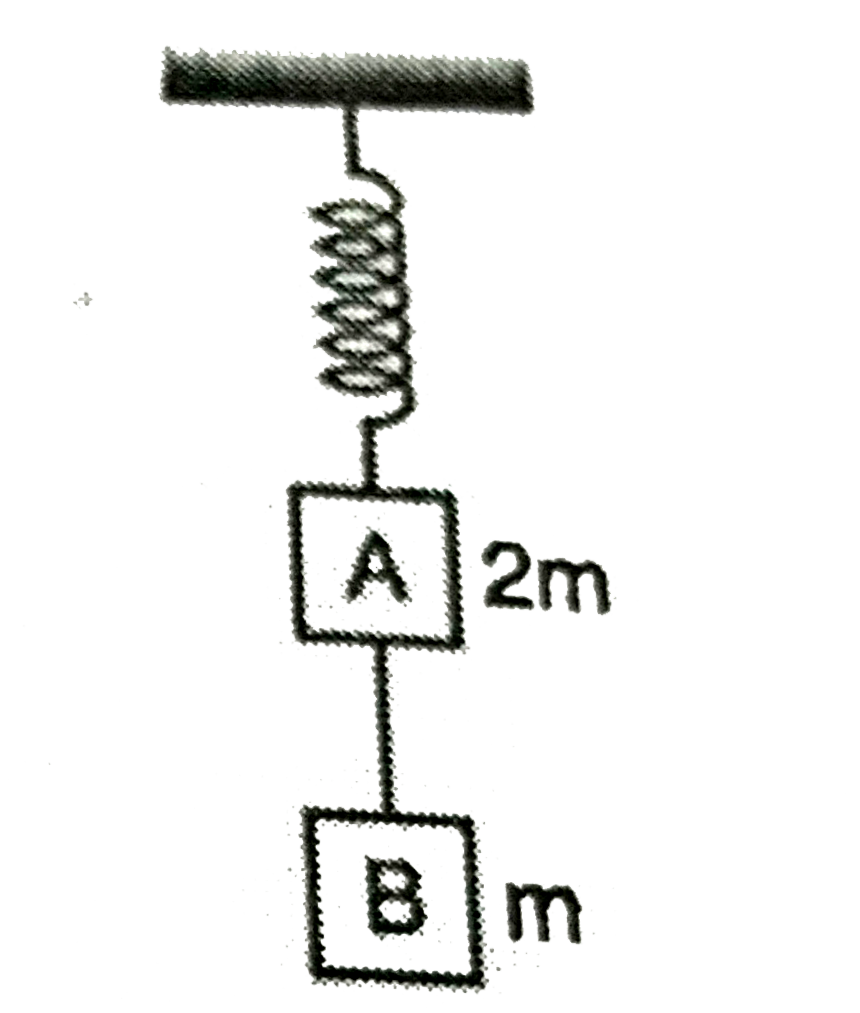
View SolutionTwo particles of mass m each are tied at the ends of a light string of length `2a`. The whole system is kept on a frictionless horizontal surface with the string held tight so that, each mass is at a distance 'a' from the center P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes `2x`, is :

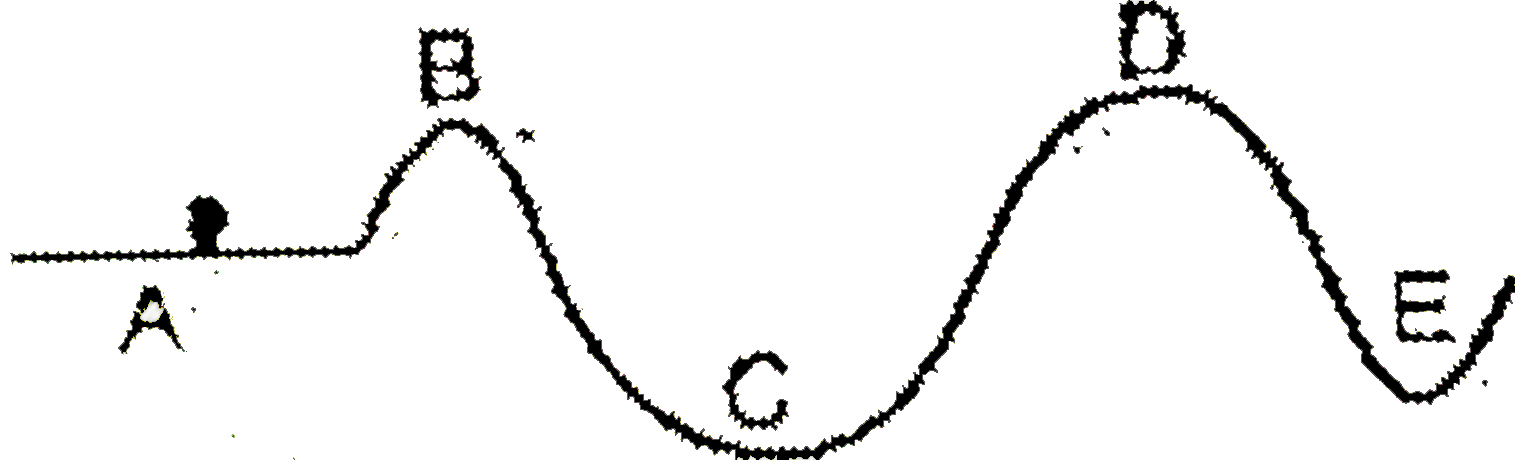
View SolutionA particle moves along on a road with constant speed at all points as shown in figure. The normal reaction of the road on the particle is :
View SolutionA particle of mass m rotates with a uniform angular speed `omega`. It is viewed from a frame rotating about the Z-axis with a uniform angular speed `omega_0`. The centrifugal force on the particler is
View SolutionA particle of mass `m_(1)` is fastened to one end of a massless string and another particle of mass `m_(2)` is fastened to the middle point of the same string. The other end of the string being fastened to a fixed point on a smooth horizontal table. The particles are then projected, so that the two particles and the string are always in the same straight line and describe horizontal circles. Then, the ratio of rotations in the two parts of the string is :
View SolutionA small block of mass `m` is released from rest from point `A` inside a smooth hemisphere bowl of radius `R`, which is fixed on group such that `OA` is horizontal. The ratio `(x)` of magnitude of centripetal force and normal reaction on the block at any point `B` varies with `theta` as :

View SolutionA partical of mass `m` oscillates along the horizontal diameter `AB` inside a smooth spherical `AB` inside a smooth sperical shell of radius `R`. At any instate `K.E.` of the partical is `K`. Then force applied by partical on the on the shell at this instant is:

View SolutionA particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration `a_(c)` is varying with time t as `a_(c) = k^(2)rt^(2)`, where k is a constant. The power delivered to the particle by the forces acting on it is :
View SolutionA long horizontal rod has a bead which can slide along its length and is initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with a constant angular acceleration, `alpha`. If the coefficient of friction between the rod and bead is `mu`, and gravity is neglected, then the time after which the bead starts slipping is :
View SolutionIn gravity free space, a particle is in constant with the inner surface of a hallow cylinder and moves in a circular path along the surface. There is some friction between the particles and the surface. The retardation of the particle is :
View SolutionA curved section of a road is banked for a speed `v`. If there is no friction between the road and the tyres then.
View SolutionIn a circular motion of a particle the tangential acceleration of the particle is given by `a_(t) = 2t m//s^(2)`. The radius of the circle described is `4m`. The particle is initially at rest. Time after which total acceleration of the particle makes `45^(@)` with radial acceleration is :
View SolutionA particle travels along the arc of a circle of radius `r`. Its speed depends on the distance travelled `l` as `v=asqrtl` where 'a' is a constant. The angle `alpha` between the vectors of net acceleration and the velocity of the particle is
View SolutionA particle of mass m is attached to one end of string of length l while the other end is fixed to point `h(h lt l)` above a horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p, if the particle is to be in contact with the table, is : `(l gt h)`
View SolutionA stone is thrown horizontally with a velocity of `10 m//s` at `h = 0`. The radius of curvature of the stone's trajectory at `t = 3s` is : [Take `g = 10 m//s^(2)`]
View SolutionThe narrow tube AC forms a quarter circles in a vertical plane. A ball B has an area of cross-section slighly smaller than that of the tube and can move without friction through it. B is placed at A and displaced slightly. During the motion from A to C it will :

View Solutiona particle is moving in a circle of radius R in such a way that at any instant the normal and the tangential component of its acceleration are equal. If its speed at `t=0` is `v_(0)` then time it takes to complete the first revolution is `R/(alphav_(0))(1-e^(-betapi))`. Find the value of `(alpha+beta)`.
View SolutionA particle P is moving in a circle of radius r with a uniform speed u. C is the centre of the circle and AB is diameter. The angular velocity of P about A and V are in the ratio :
View SolutionA small body of mass m can slide without friction along a through bent which is in the form of a semi-circular arc of radius R. At what height h will the body be at rest with respect to the trough, if the trough rotates with uniform angular velocity `omega` about a vertical axis:

View SolutionA car moves along a horizontal circular road of radius r with constant speed v. The coefficient of friction between the wheels and the road is `mu`. Which of the following statement is not true ?
View SolutionA smooth hollow cone whose vertical angle is `2alpha` with its axis vertical and vertex downwards revolves about its axis `eta` time per seconds. A particle is placed on the inner surface of cone so that it rotates with same speed. The radius of rotation for the particle is :
View SolutionA particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is `20 cm//s` & acceleration is `20 cm//s^(2)`. The particle is now shifted to a new position to make the radius half of the original value. The new values of the speed & acceleration will be:
View SolutionA particle of mass m is suspended from a fixed O by a string of length L. At `t = 0`, it is displaced from its equilibrium position and released. The graph which shows the variation of the tension T in the string with time t is :

View SolutionA rod of length L is pivoted at one end and is rotated with as uniform angular velocity in a horizontal plane. Let `T_1 and T_2` be the tensions at the points L//4 and 3L//4 away from the pivoted ends.
View SolutionThe driver of a car-travelling at speed V suddenly sees a wall at a distance r directly infront of him. To avoid collision. He should :
View SolutionA body is undergoing uniform circular motion then which of the following quantity is constant
View SolutionA particle is resting on an inverted cone as shown. It is attached to cone by a thread of length 20 cm. String remains parallel to slope of cone. The cone is givenangular acceleration of `0.5 rad//sec^(2)` then at what time does mass leave contact with surface (assuming sufficient friction) :
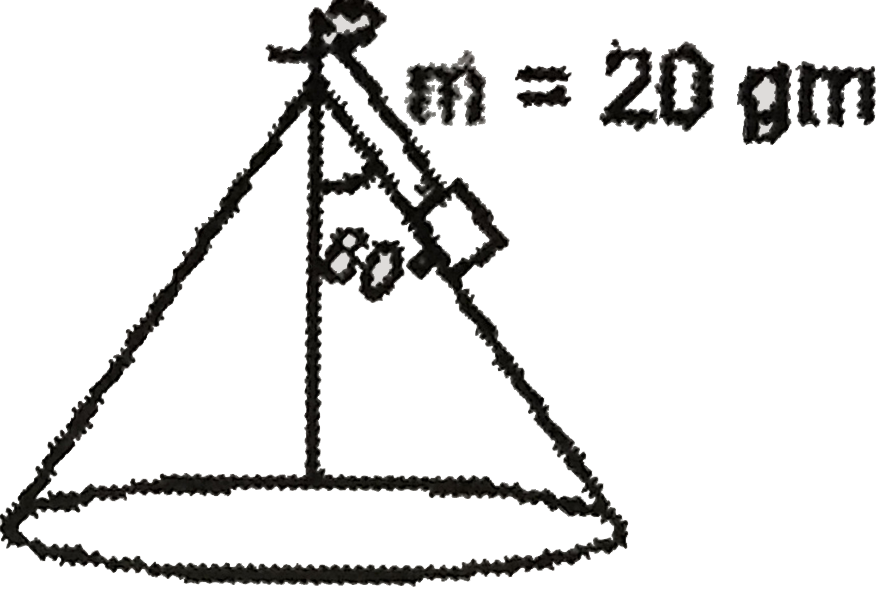
View SolutionA particle initially at rest is released from A as shown in figures. The approximate variation of direction of resultant acceleration as particle moves from A to B is :

View SolutionRepeat above Question 3, if the charge is negative and the angle made by the boundary with the velocity is `theta = pi/6.`
View SolutionTwo similar trains are moving along the equational line with same speed but in opposite direction. Then :
View SolutionTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
View SolutionIndicate the direction of frictional force on a car which is moving along the curved path with non zero tangential acceleration, in anti-clock direction:
View Solution
level 1 questions and complete solutions for chapter FORCE ANALYSIS of SHREE BALAJI PHYSICS (HINGLISH) of Class 11