Complete Solutions to Level-3 of chapter FORCE ANALYSIS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FORCE ANALYSIS |
| ANURAG MISHRA | Level-3 |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
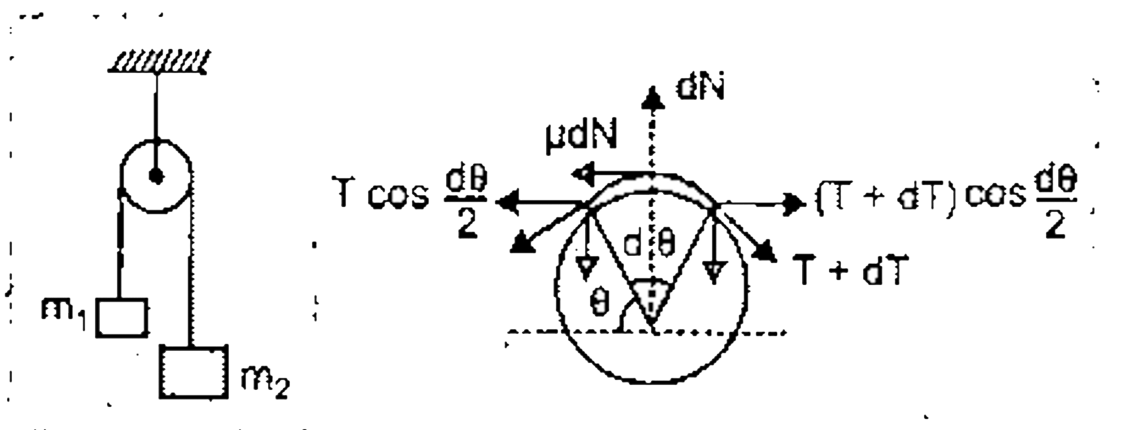
Effect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient `mu`. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
`dN=(T+dT) "sin" (d theta)/2+T "sin"(d theta)/2`

`(T+dT)"cos"(d theta)/2 -T"cos"(d theta)/2-mu dN=dr a=0` (massless strings)
`dT"cos"(d theta)/2=mu dN`
`dT"cos"(d theta)/2=mu [(T+dt) "sin" (d theta)/2+T "sin" (d theta)/2]`
`dt."cos" (d theta)/2=mu[T "sin" (d theta)/2+dT. "sin" (d theta)/2+T "sin" (d theta)/2]`
`dT=mu[T. (d theta)/2+0+T(d theta)/2]=mu T cos theta`
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)`
Suppose cofficient of friction between the string and pulley is `mu =1/pi`
What should be the ratio of heavier mass to lighter mass for no motion ?
View SolutionEffect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient `mu`. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
`dN=(T+dT) "sin" (d theta)/2+T "sin"(d theta)/2`
`(T+dT)"cos"(d theta)/2 -T"cos"(d theta)/2-mu dN=dr a=0` (massless strings)
`dT"cos"(d theta)/2=mu dN`
`dT"cos"(d theta)/2=mu [(T+dt) "sin" (d theta)/2+T "sin" (d theta)/2]`
`dt."cos" (d theta)/2=mu[T "sin" (d theta)/2+dT. "sin" (d theta)/2+T "sin" (d theta)/2]`
`dT=mu[T. (d theta)/2+0+T(d theta)/2]=mu T cos theta`
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)`
Suppose cofficient of friction between the string and pulley is `mu =1/pi`
If `m_(2)=2em` then acceleration of each mass is :
View SolutionEffect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient `mu`. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
`dN=(T+dT) "sin" (d theta)/2+T "sin"(d theta)/2`

`(T+dT)"cos"(d theta)/2 -T"cos"(d theta)/2-mu dN=dr a=0` (massless strings)
`dT"cos"(d theta)/2=mu dN`
`dT"cos"(d theta)/2=mu [(T+dt) "sin" (d theta)/2+T "sin" (d theta)/2]`
`dt."cos" (d theta)/2=mu[T "sin" (d theta)/2+dT. "sin" (d theta)/2+T "sin" (d theta)/2]`
`dT=mu[T. (d theta)/2+0+T(d theta)/2]=mu T cos theta`
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)`
Suppose cofficient of friction between the string and pulley is `mu =1/pi`
The tension on side ofheavier\nass will be:
View SolutionEffect of friction between pulley and thread :
In ideal cases i.e., when pulley and strings are massless and no friction exists at any contact surface, then tension in the string is constant throughout its length. But consider a, massless pulley and massless string but friction exists between pulley and string With coefficient `mu`. Then tension at the two ends of the pulley will be different. As shown in figure, consider an element of string :
`dN=(T+dT) "sin" (d theta)/2+T "sin"(d theta)/2`
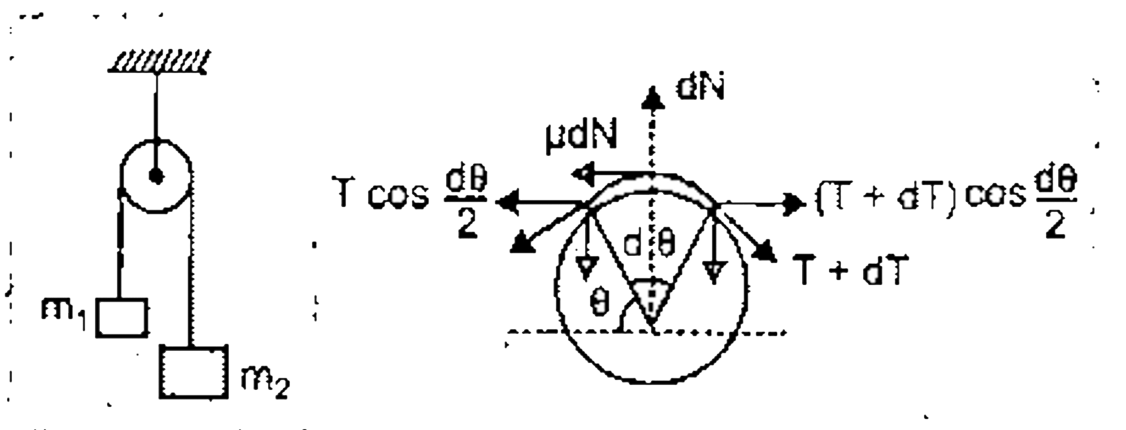
`(T+dT)"cos"(d theta)/2 -T"cos"(d theta)/2-mu dN=dr a=0` (massless strings)
`dT"cos"(d theta)/2=mu dN`
`dT"cos"(d theta)/2=mu [(T+dt) "sin" (d theta)/2+T "sin" (d theta)/2]`
`dt."cos" (d theta)/2=mu[T "sin" (d theta)/2+dT. "sin" (d theta)/2+T "sin" (d theta)/2]`
`dT=mu[T. (d theta)/2+0+T(d theta)/2]=mu T cos theta`
int_(T_(1))^(T_(2)) (d T)/T=int _(0)^(pi)mu d theta rArr ln(T_(2)/T_(1))=mu pi rArrT_(2)/T_(1)=e^(mu pi)`
Suppose cofficient of friction between the string and pulley is `mu =1/pi`
The tension on side of lighter mass will be:
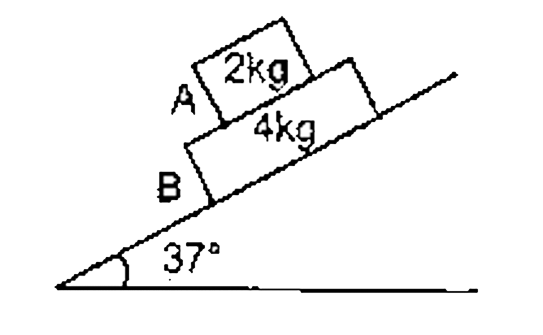
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`
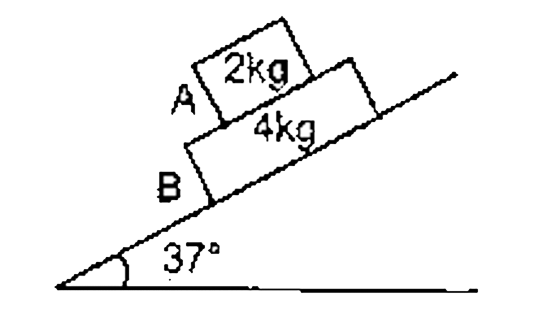
If `mu_(1)=0.8, mu_(2)=0.8` then :
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`
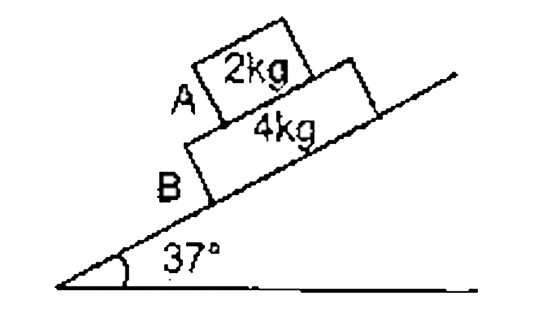
In the previous question the frictional force between block B and plane is :
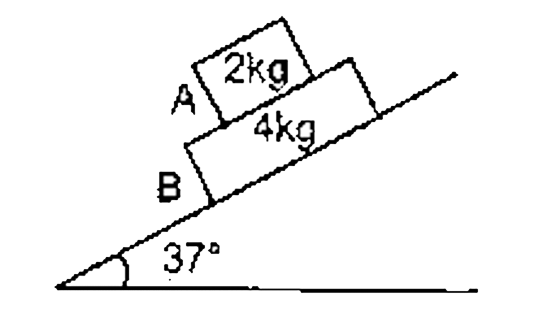
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`
If `mu_(1)=0.5, mu_(2)=0.5` then :
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`

The frictional force acting between the two blocks in the previous question is :
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`
If `mu_(1)=0.4, mu_(2)=0.5` then:
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`

The frictional force acting between the blocks in the previous case will be:
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`

If `mu_(1)=0.5, mu_(2)=0.4` then:
View Solutionconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination `37^(@)` with horizontal. The coefficient of friction between block B and inclined plane is `mu_(2)` and in between the two, blocks is `mu_(1)`. The system is released from rest.
`("Take "g=10m//sec^(2))`

The frictional force acting between the blocks in the previous case :
View SolutionIn the given figure, the blocks of mass `2 kg` and `3 kg` are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t`( where `'t' "in" sec`) is applied on upper block in the direction shown. Based on above data answer the following questions.
`( g= 10m//sec^(2))`
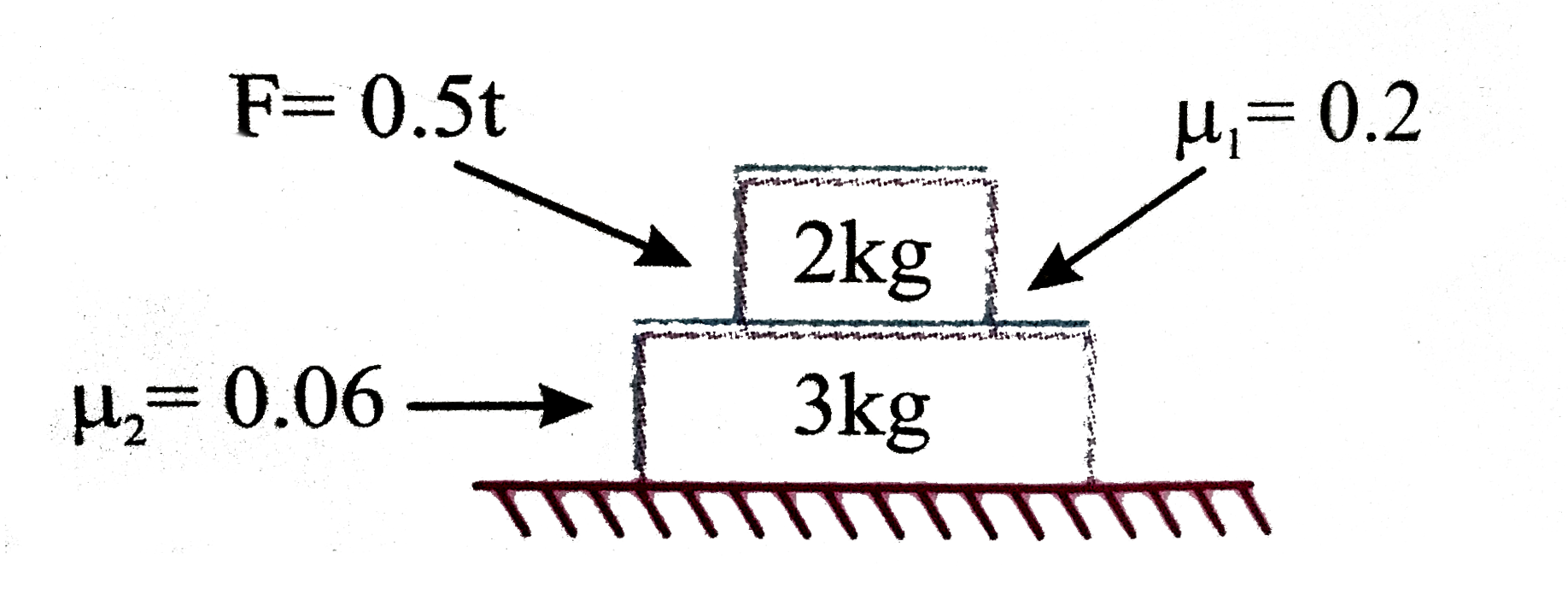
The motion of blocks `2 kg` and `3 kg` will begin at time `t = -, -` respectively
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`
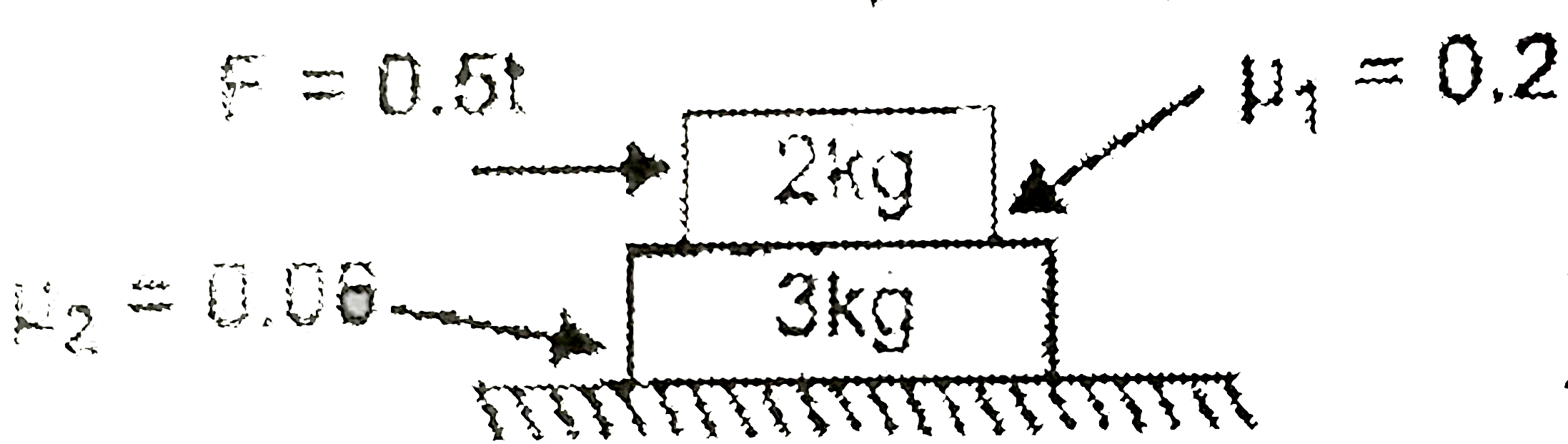
The realtive slipping between the blocks occurs at `t=`
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`
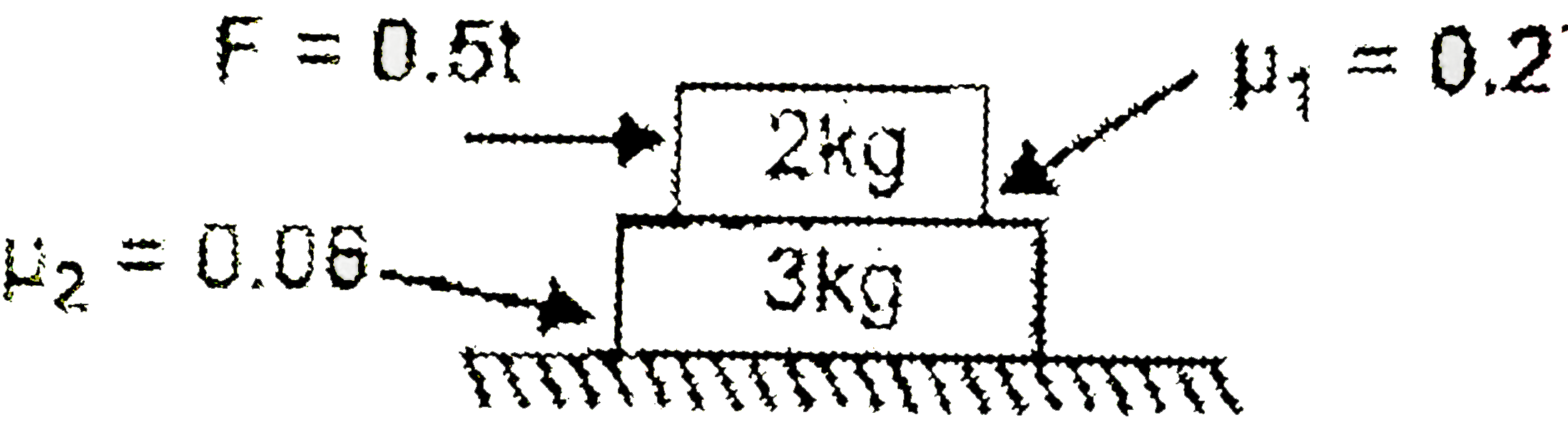
The frictional force acting between the two blocks at `t=9` sec
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`
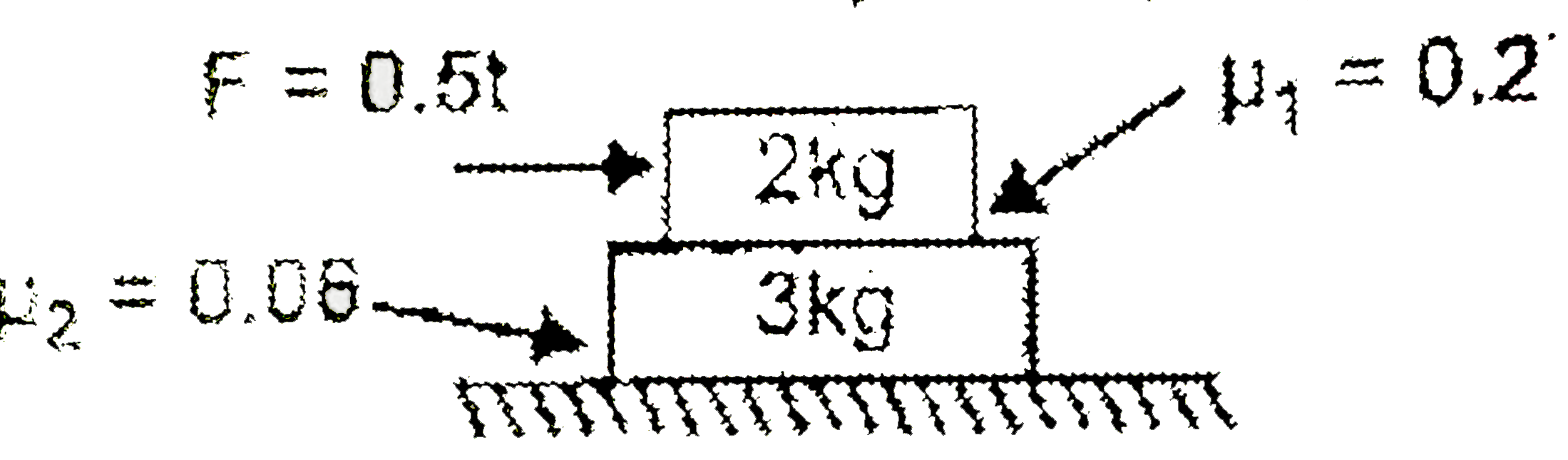
The frictional force acting between the blocks at `t=10 sec` is
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`
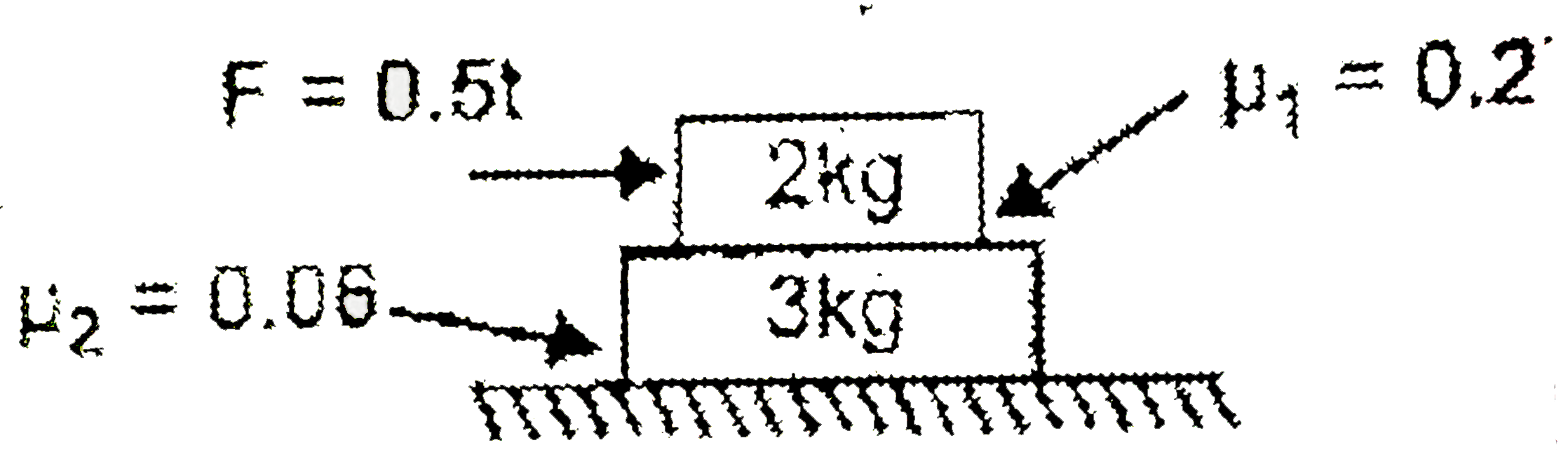
The acceleration time graph for 2kg blok is :
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`
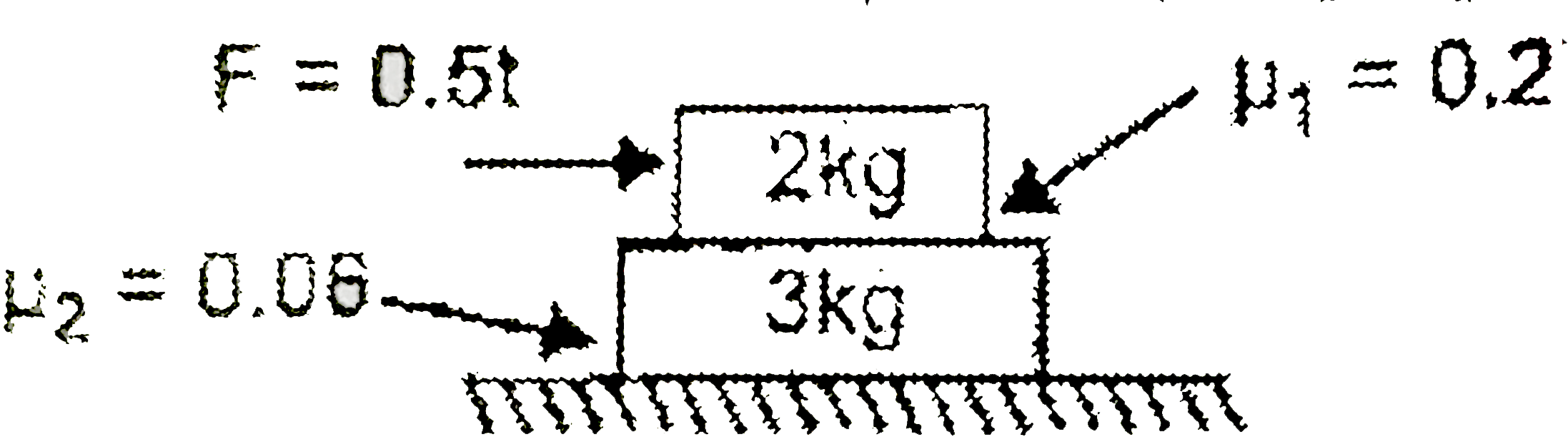
The acceleration time graph for 4 kg block is :
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`
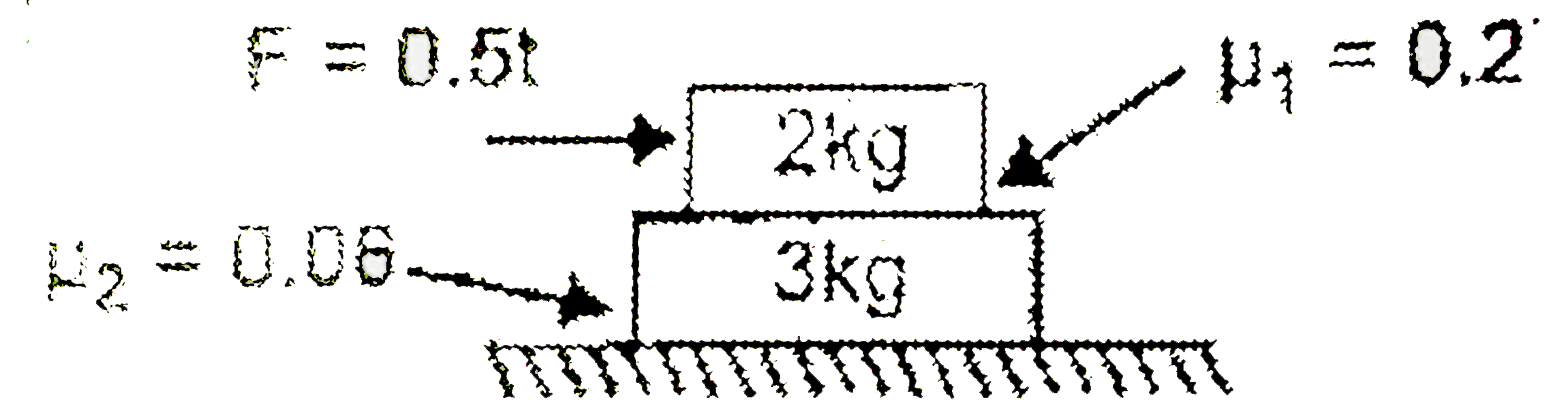
The frictional force acting between 3 kg block and ground w.r.t. time will vary as :
View SolutionIn the given figure, the blocks of mass 2kg and 3kg are placed one over the other as shown. The surface are rough with coefficient of friction `mu_(1)=0.2, mu_(2)=0.06`. A force `F=0.5t` (where 't' in sec) is applied on upper block in the direction shown. Based on above data answers the following questions. `(g = 10 m//sec^(2))`

The friction force between the blocks and time graph is :
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with `x` as `mu = kx`, where `k = tan theta`. A block is released at O
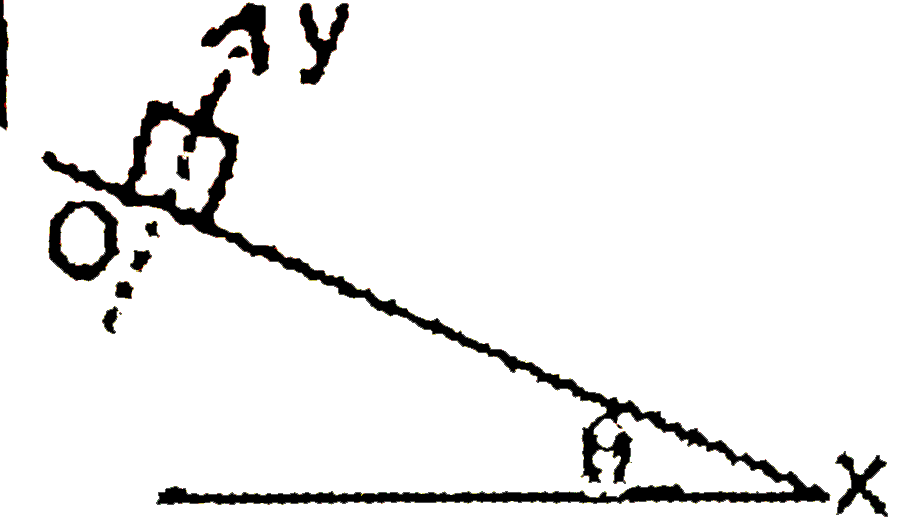
The maximum velocity of block will be :
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with `x` as `mu = kx`, where `k = tan theta`. A block is released at O
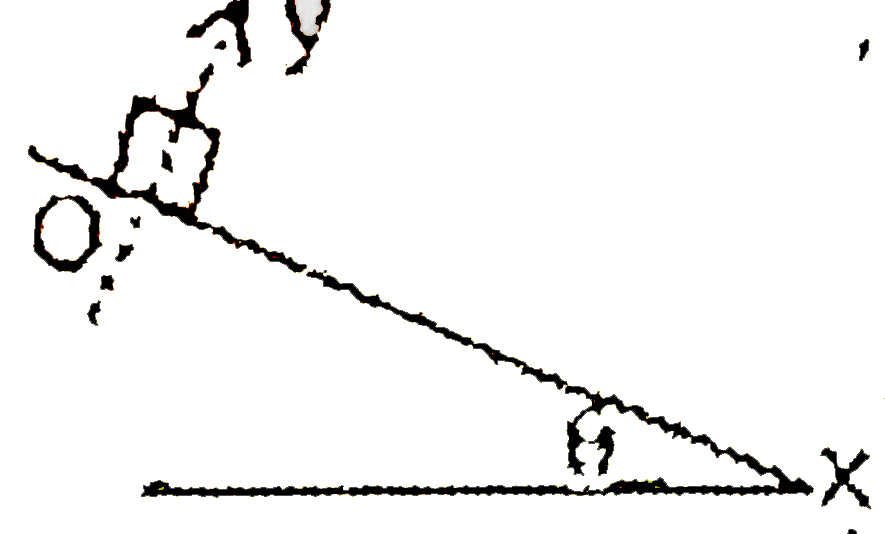
Maximum distance traveled by the block :
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with `x` as `mu = kx`, where `k = tan theta`. A block is released at O
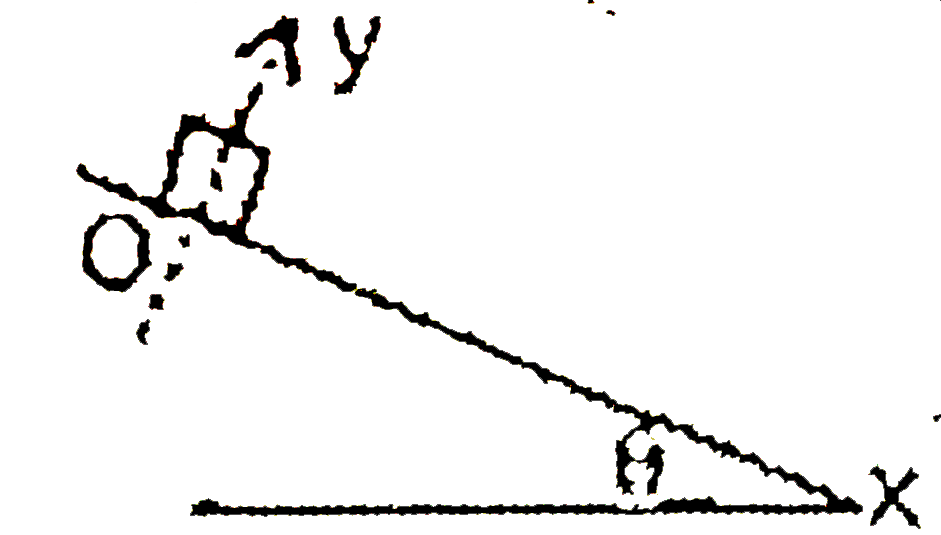
Frictional force acting on the block after it comes to rest :
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with `x` as `mu = kx`, where `k = tan theta`. A block is released at O
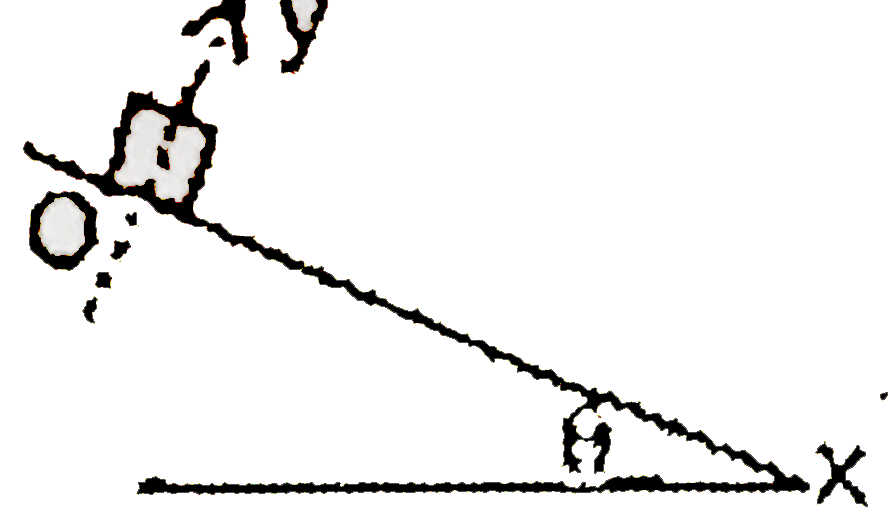
Frictional acting on the block just before it comes to rest :
View SolutionThe figure shows a rod which startsm rotating with angular acceleration `alpha` about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass `m` just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient `mu`. As the angular velocity of rod increases the bead starts sliding over the rod (say after time `t_(0)`)
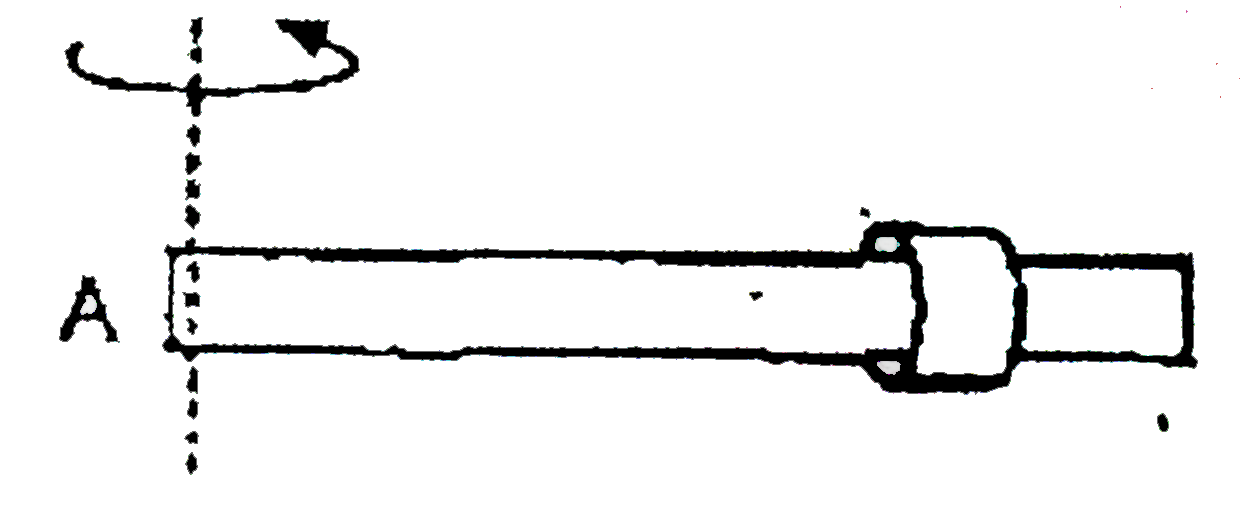
Based on above information answer the following question :
The normal force acting on bead at time `t (lt t_(0))` is :
View SolutionThe figure shows a rod which startsm rotating with angular acceleration `alpha` about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass `m` just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient `mu`. As the angular velocity of rod increases the bead starts sliding over the rod (say after time `t_(0)`)

Based on above information answer the following question :
Friction force acting on bead at time `t( lt t_(0))` is given by :
View SolutionThe figure shows a rod which startsm rotating with angular acceleration `alpha` about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass `m` just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient `mu`. As the angular velocity of rod increases the bead starts sliding over the rod (say after time `t_(0)`)
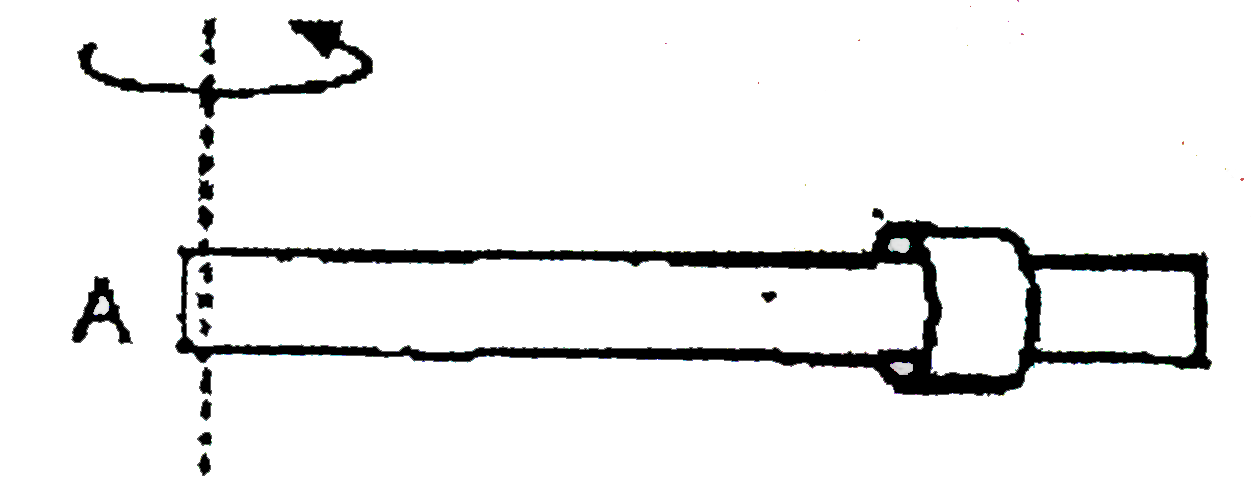
Based on above information answer the following question :
If the bead start sliding at `t=t_(0)` then value of `t_(0)` is given by :
View SolutionA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity `omega`. The wall of funnel makes an angle `37^(@)` with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is `mu` (Take `g = 10 m//s^(2)`)

The friction force acting between the block and surface (if `mu = 0.3`) of funnel at `omega = 5 rad//s` is :
View SolutionA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity `omega`. The wall of funnel makes an angle `37^(@)` with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is `mu` (Take `g = 10 m//s^(2)`)

For what value of `omega`, there would be no frictional force acting between the surfaces :
View SolutionA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity `omega`. The wall of funnel makes an angle `37^(@)` with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is `mu` (Take `g = 10 m//s^(2)`)

The maximum value of angular velocity for which no relative slipping occur and also direction of frictional force is : (take `mu = 2//3`)
View SolutionA very small cube of mass 2kg is placed on the surface of a funnel as shown in figure. The funnel is rotating about its vertical axis of symmetry with angular velocity `omega`. The wall of funnel makes an angle `37^(@)` with horizontal. The distance of cube from the axis of rotation is 20 cm and friction coefficient is `mu` (Take `g = 10 m//s^(2)`)
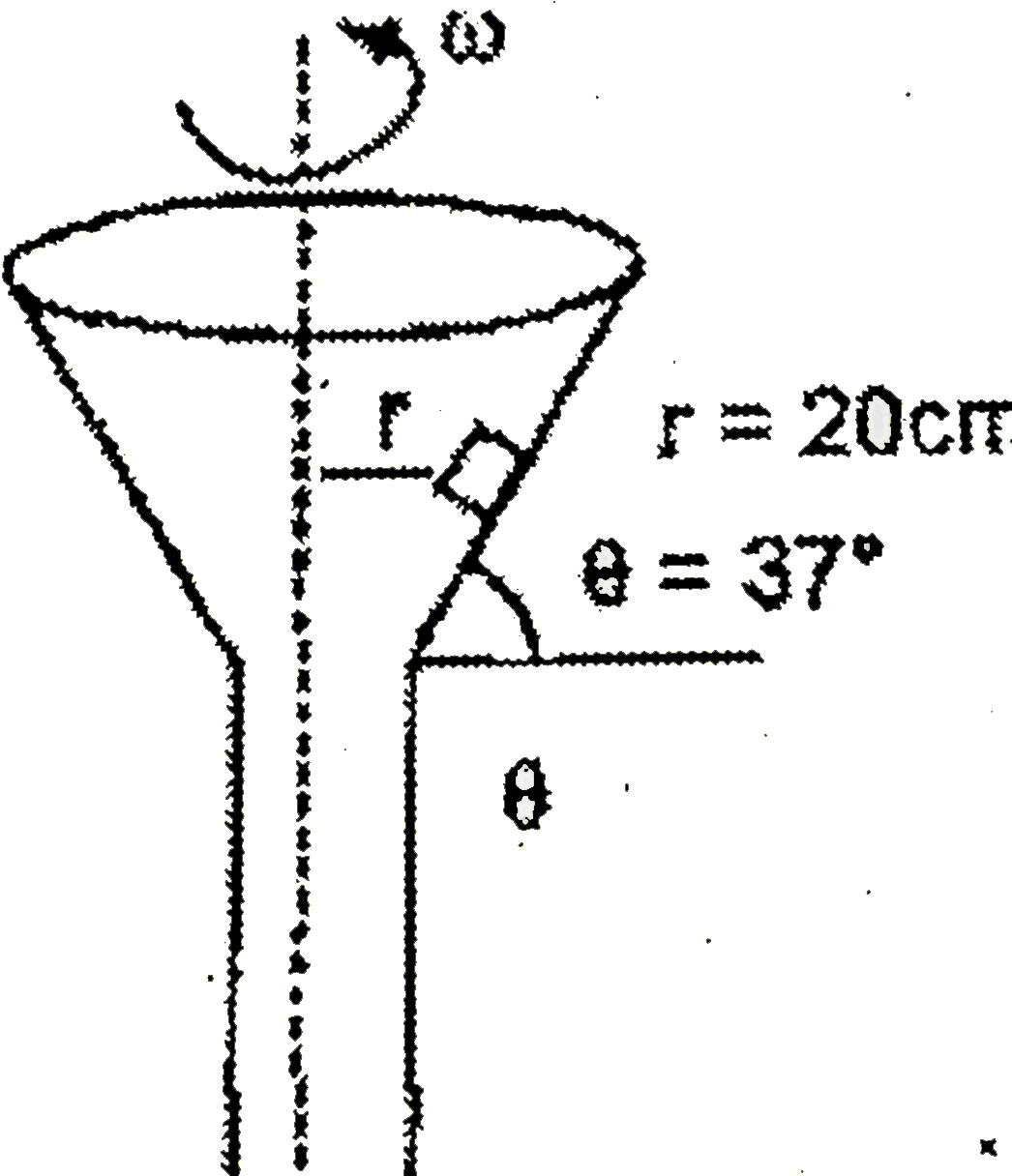
The mimimum value of angular velocity for which relative slipping occurs and also the direction of frictional force acting `mu = 2//3` :
View SolutionA car is moving with speed `v` and is taking a turn on a circular road of radius 10 m. The angle of banking is `37^(@)`. The driver wants that car does not slip on the road. The coefficient of friction is `0.4 (g = 10 m//sec^(2))`
The speed of car for which no frictional force is produced is :
View SolutionA car is moving with speed `v` and is taking a turn on a circular road of radius 10 m. The angle of banking is `37^(@)`. The driver wants that car does not slip on the road. The coefficient of friction is `0.4 (g = 10 m//sec^(2))`
The friction force acting when `v=10 m//sec` and mass of car is 50 kg is :
View SolutionA car is moving with speed `v` and is taking a turn on a circular road of radius 10 m. The angle of banking is `37^(@)`. The driver wants that car does not slip on the road. The coefficient of friction is `0.4 (g = 10 m//sec^(2))`
If the car were moving on a flat road and distance between the front tyres is 2 m and the height of the centre of the mass of the car is 1m from the ground, then, the minimum velocity for which car topples is :
View SolutionA body of mass `m=1.8 kg` is placed on an inclined plane, the angle of inclination is `alpha = 37^(@)`, and is attached to the top end of the slope with a thread which is parallel to the slop. Then the slope is moved with a horizontal acceleration of a. Fraction is negligible.
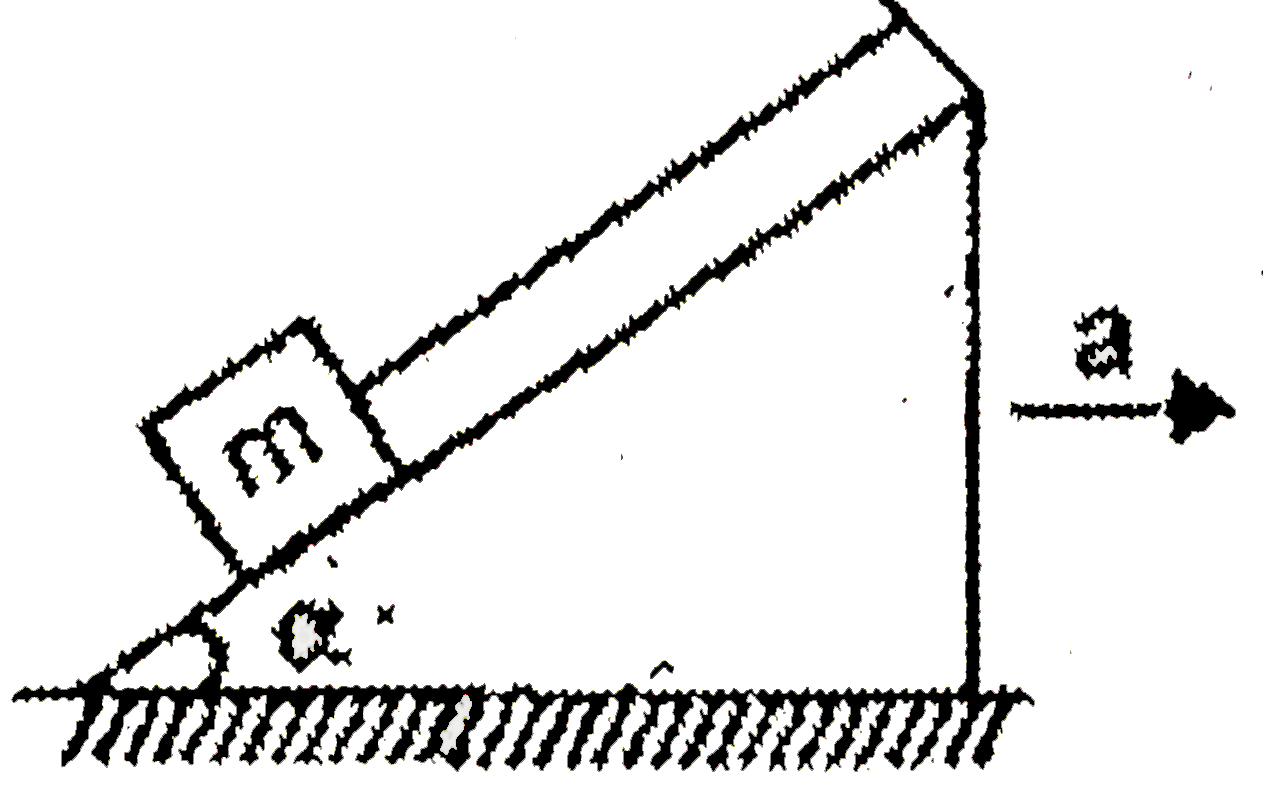
The acceleration, if the body pushes the slope with a force of `(3)/(4) mg` is :
View SolutionA body of mass `m=1.8 kg` is placed on an inclined plane, the angle of inclination is `alpha = 37^(@)`, and is attached to the top end of the slope with a thread which is parallel to the slop. Then the slope is moved with a horizontal acceleration of a. Fraction is negligible.

The tension in thread is :
View SolutionA body of mass `m=1.8 kg` is placed on an inclined plane, the angle of inclination is `alpha = 37^(@)`, and is attached to the top end of the slope with a thread which is parallel to the slop. Then the slope is moved with a horizontal acceleration of a. Fraction is negligible.

At what acceleration will the body lose contact with plane :
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string `T_(1)`. Two masses of `m_(1) and m_(2)` are connected with inextensible light string and tension in this string `T_(2)` as shown in figure. Read the questionbs carefully and answer
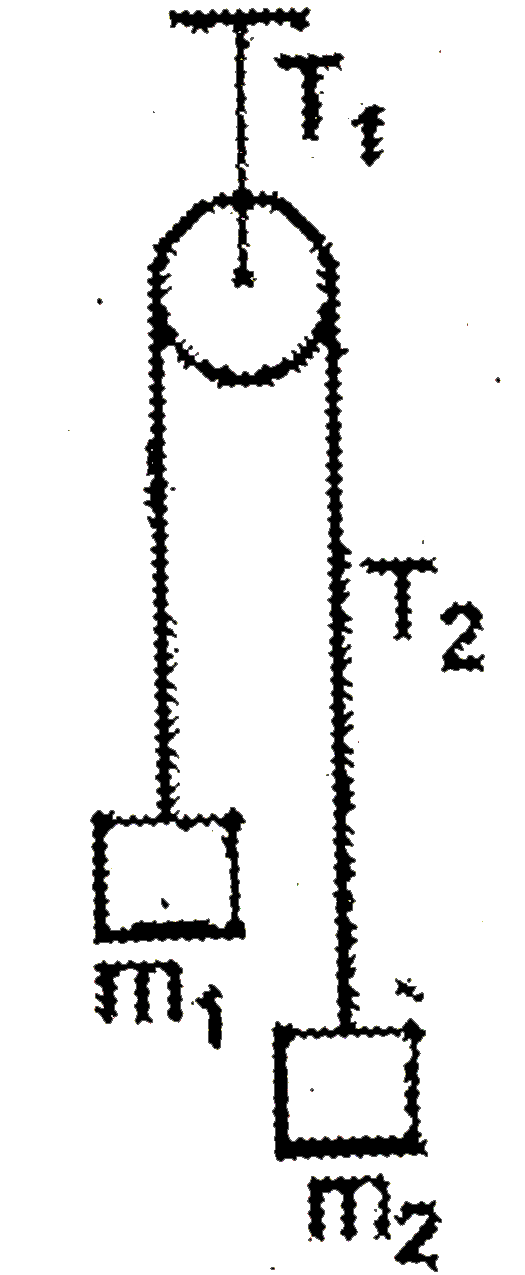
If `m_(1)+m_(2)=m` and lift is moving with constant velocity then value of `T_(1)` :
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string `T_(1)`. Two masses of `m_(1) and m_(2)` are connected with inextensible light string and tension in this string `T_(2)` as shown in figure. Read the questionbs carefully and answer

If `m_(1)` is very small as compared to `m_(2)` and lift is moving with constant velocity then value of `T_(2)` is nearly :
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string `T_(1)`. Two masses of `m_(1) and m_(2)` are connected with inextensible light string and tension in this string `T_(2)` as shown in figure. Read the questionbs carefully and answer
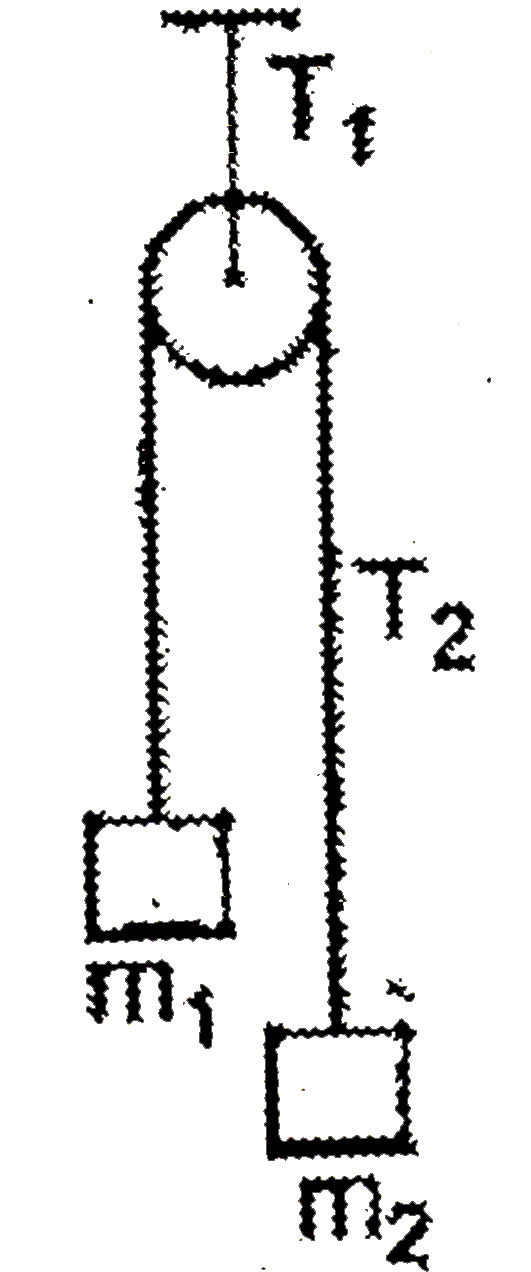
If `m_(1)=m_(2) and m_(1)` is moving at a certain instant with velocity `v` upward with respect to lift and the lift is moving in upward direction with constant acceleration `(a lt g)` then speed of `m_(1)` with respect to lift :
View SolutionA shot putter with a mass of 80 kg pushes the iron ball of mass of 6 kg from a standing position accelerating it uniformly from rest at an angle of `45^(@)` with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it is 2m high above the level, ground and hits the ground 2 seconds later.
The acceleration of the ball in shot putter's hand :
View SolutionA shot putter with a mass of 80 kg pushes the iron ball of mass of 6 kg from a standing position accelerating it uniformly from rest at an angle of `45^(@)` with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it is 2m high above the level, ground and hits the ground 2 seconds later.
The horizontal distance between the point of release and the point where the ball hits the ground :
View SolutionA shot putter with a mass of 80 kg pushes the iron ball of mass of 6 kg from a standing position accelerating it uniformly from rest at an angle of `45^(@)` with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it is 2m high above the level, ground and hits the ground 2 seconds later.
The minimum value of the static coefficient of frictin if the shot putter does not slip during the shot is closet to :
View SolutionIn the figure shown, the mass of the trolley is 100 kg and it can move without friction on the horizontal floor. It length is 12 cm. The mass of the girl is 50 kg. Friction exists between is 12 m. The mass of the girl is 50 kg. Friction exists between the shoes of the girl and the trolley's upper surface, with `mu = 1//3`, The girl can run with a maximum speed `= 9 m//s` on the surface of the trolley, with respect to the surface `= 9 m//s` on the surface of thr trolley, with respect to the surface. At `t=0` the girlm starts running from left to the right. The trolley was initially stationary. `(g = 10 m//s^(2))`
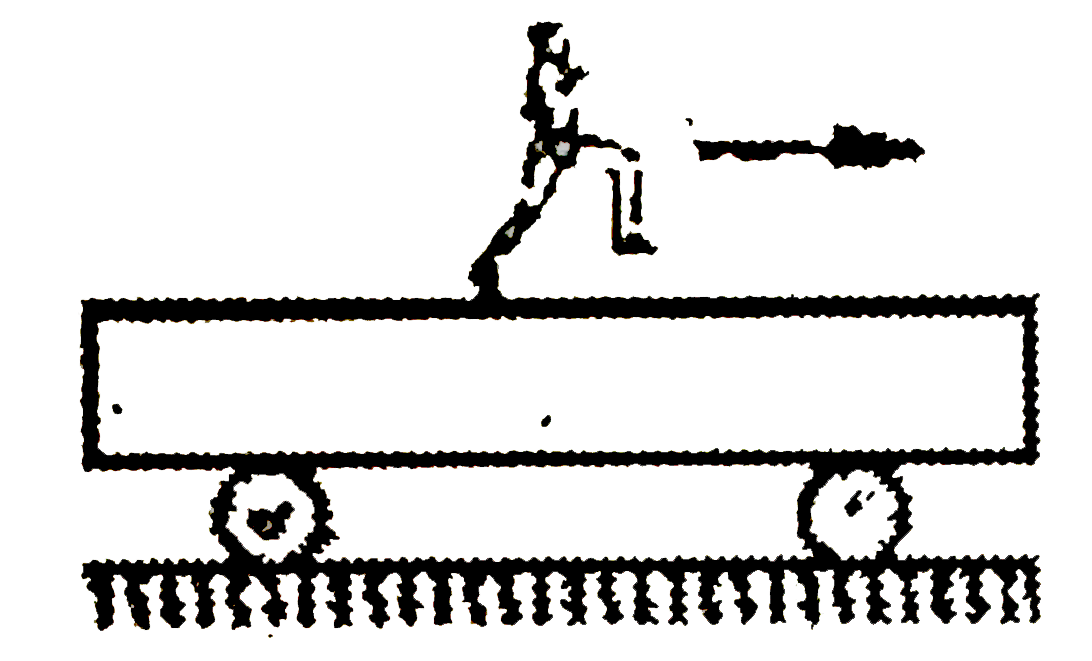
The minimum time in which the girl can acquire her maximum speed, for no slipping is :
View SolutionIn the figure shown, the mass of the trolley is 100 kg and it can move without friction on the horizontal floor. It length is 12 cm. The mass of the girl is 50 kg. Friction exists between is 12 m. The mass of the girl is 50 kg. Friction exists between the shoes of the girl and the trolley's upper surface, with `mu = 1//3`, The girl can run with a maximum speed `= 9 m//s` on the surface of the trolley, with respect to the surface `= 9 m//s` on the surface of thr trolley, with respect to the surface. At `t=0` the girlm starts running from left to the right. The trolley was initially stationary. `(g = 10 m//s^(2))`
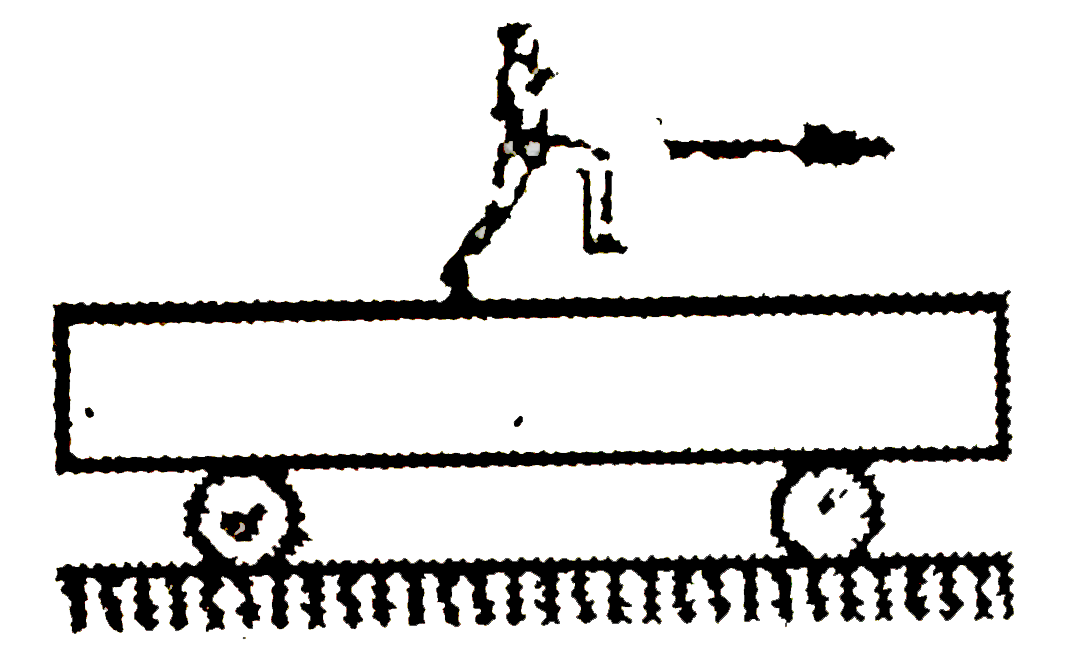
The total kinetic energy of system (trolley + girl) at the instant the girl acquires her maximum relative speed with respect to trolley, is :
View SolutionIn the figure shown, the mass of the trolley is 100 kg and it can move without friction on the horizontal floor. It length is 12 cm. The mass of the girl is 50 kg. Friction exists between is 12 m. The mass of the girl is 50 kg. Friction exists between the shoes of the girl and the trolley's upper surface, with `mu = 1//3`, The girl can run with a maximum speed `= 9 m//s` on the surface of the trolley, with respect to the surface `= 9 m//s` on the surface of thr trolley, with respect to the surface. At `t=0` the girlm starts running from left to the right. The trolley was initially stationary. `(g = 10 m//s^(2))`
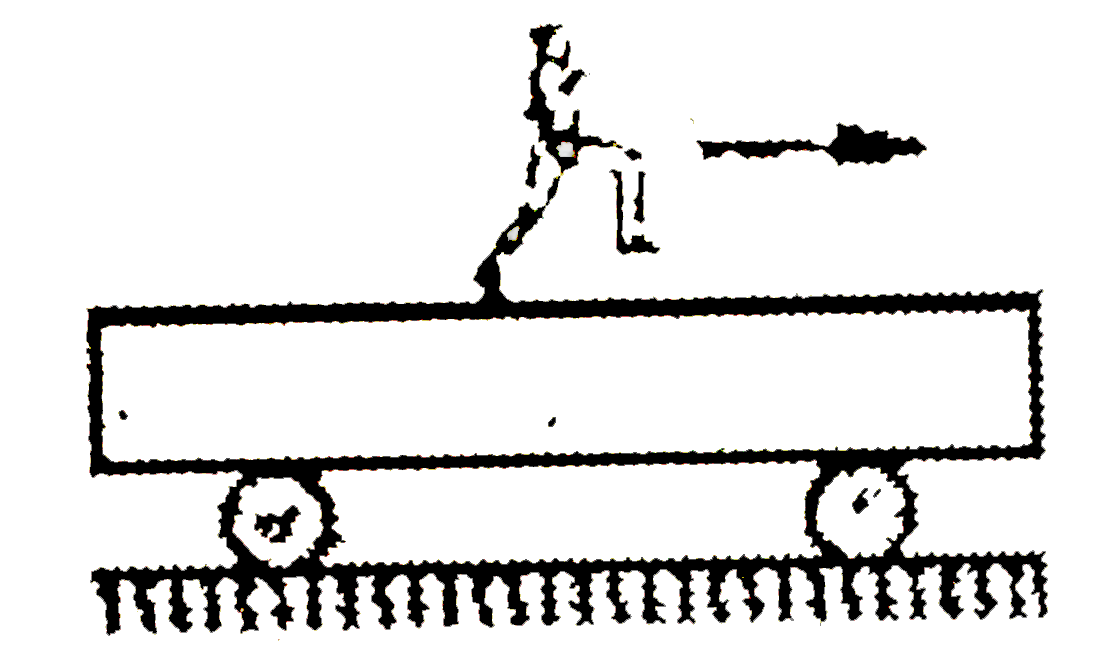
The displacement of the trolley by the time the girl reaches the right end of the trolley is :
View SolutionIn the figure shown, the mass of the trolley is 100 kg and it can move without friction on the horizontal floor. It length is 12 cm. The mass of the girl is 50 kg. Friction exists between is 12 m. The mass of the girl is 50 kg. Friction exists between the shoes of the girl and the trolley's upper surface, with `mu = 1//3`, The girl can run with a maximum speed `= 9 m//s` on the surface of the trolley, with respect to the surface `= 9 m//s` on the surface of thr trolley, with respect to the surface. At `t=0` the girlm starts running from left to the right. The trolley was initially stationary. `(g = 10 m//s^(2))`

The minimum time in which the girl can stop from 9 m/s relative speed, to zero relative speed, without causing her shoes to slip is :
View SolutionIn the figure shown, the mass of the trolley is 100 kg and it can move without friction on the horizontal floor. It length is 12 cm. The mass of the girl is 50 kg. Friction exists between is 12 m. The mass of the girl is 50 kg. Friction exists between the shoes of the girl and the trolley's upper surface, with `mu = 1//3`, The girl can run with a maximum speed `= 9 m//s` on the surface of the trolley, with respect to the surface `= 9 m//s` on the surface of thr trolley, with respect to the surface. At `t=0` the girlm starts running from left to the right. The trolley was initially stationary. `(g = 10 m//s^(2))`
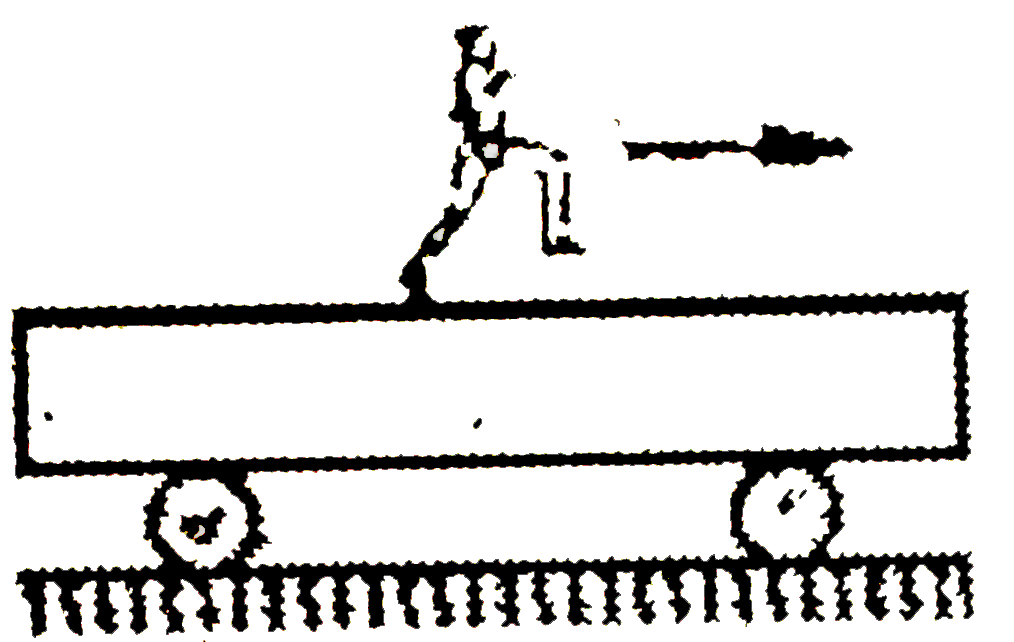
At a certain moment when the girl was accelerating, the earth frame accelerating of the trolley is found to be `1m//s^(2)`. At this moment, the friction force between the girl's shoes and the trolley's surface is :
View SolutionIn the figure shown, the mass of the trolley is 100 kg and it can move without friction on the horizontal floor. It length is 12 cm. The mass of the girl is 50 kg. Friction exists between is 12 m. The mass of the girl is 50 kg. Friction exists between the shoes of the girl and the trolley's upper surface, with `mu = 1//3`, The girl can run with a maximum speed `= 9 m//s` on the surface of the trolley, with respect to the surface `= 9 m//s` on the surface of thr trolley, with respect to the surface. At `t=0` the girlm starts running from left to the right. The trolley was initially stationary. `(g = 10 m//s^(2))`

Suppose the girl accelerates slowly, at a constant rate, and acquires the relative speed of `9 m//s` only when it reaches the right end of the trolley, then what must be the earth frame acceleration of the girl ?
View Solution
Level-3 questions and complete solutions for chapter FORCE ANALYSIS of SHREE BALAJI PHYSICS (HINGLISH) of Class 11