Complete Solutions to Level-2 of chapter FORCE ANALYSIS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FORCE ANALYSIS |
| ANURAG MISHRA | Level-2 |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
A particle stays at rest as seen in a frame. We can concude that :
View SolutionA particle is found to be at rest when seen from a frame `S_(1)` and moving with a constant velocity when seen from another frame `S_(2)`. Select the possible options :
View SolutionFigure shows a heavy block kept on a frictionless surface and being pulled on the left rope is withdrawn but the force on the right end continues to act. Let `F_1` and `F_2` be the magnitude of the forces by the right rope and the left rope on the block respectively.
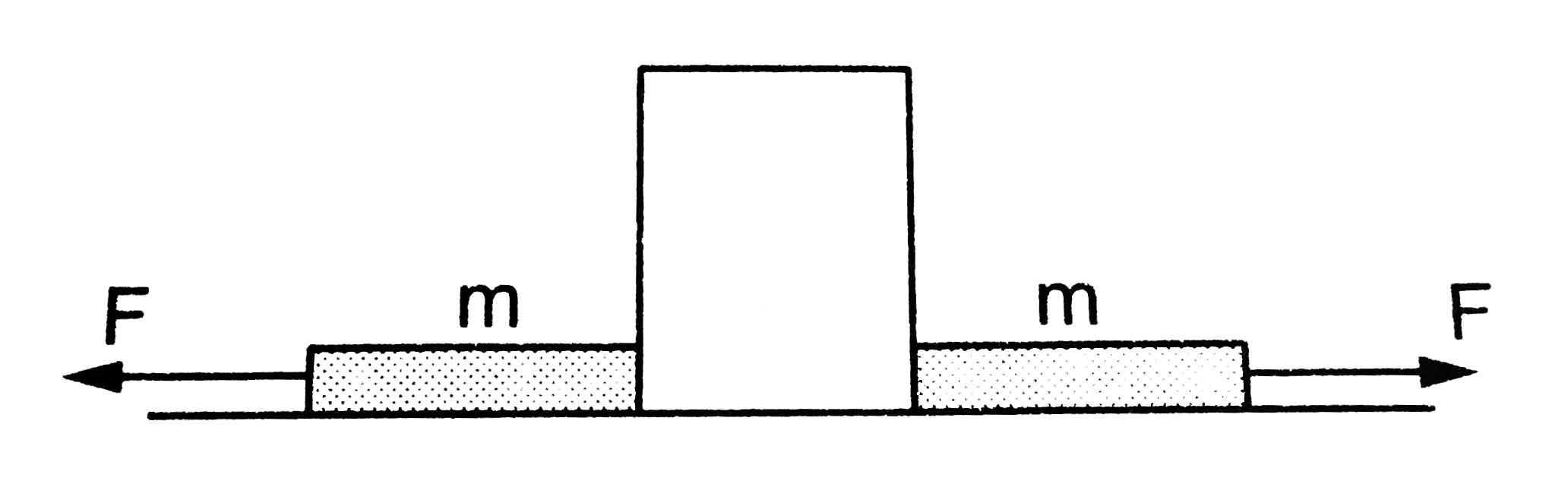
View SolutionThe force exerted by the floor of an elevator on the foot of a person standing there is more than the weight of the person if the elevator is :
View SolutionIf the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be :
View SolutionA particle is observed from two frames `S_(1) and S_(2)`. The frame `S_(2)` moves with respect to `S_(1)` with an acceleration a. Let `F_(1) and F_(2)` be the pseudo forces on the particle when seen from `S_(1) and S_(2)` respectively. Which of the following are not possible ?
View SolutionIn the arrangement shown pulley and thread are mass less. Mass of plate is 20 kg and that of boy is 30 kg.
Then :

View SolutionA smooth ring of mass `m` can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding

View SolutionA block of mass `m` is kept on an inclined plane of mass `2m` and inclination `alpha` to horizontal. If the whole system is accelerated such that the block does not slip on the wedge then :
View SolutionThe car in the given figure moves with constant velocity `v`. When `x=0` end A and B were coincident at C. Then which of the following sentences is/are correct :

View SolutionTwo men of unequal hold to the two sections of a light rope passing over a smooth light pulley. Which of the following are possible ?

View SolutionIn the situation shown in figure `F=500` newton applied on the pulley `m_(1)=50 kg and m_(2) = 10 kg` and pulley and strings are massless and frictionless. Then the acceleration of the pulley is : `[g = 10 m//s^(2)]`
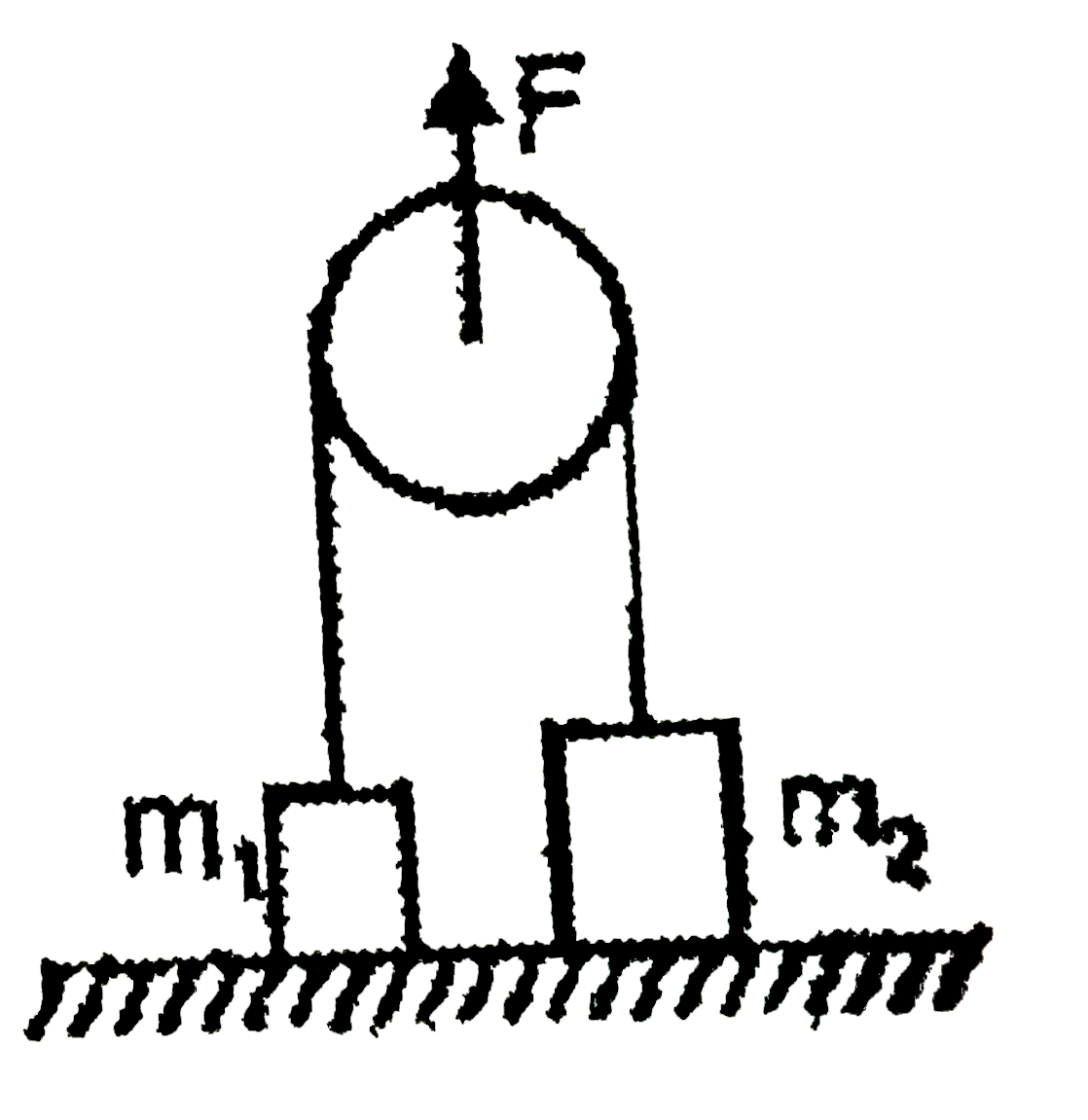
View SolutionIn the figure, the pulley P moves to the right with a constant speed `u`. The downward speed of A is `v_(A)`, and the speed of B to the right is `v_(B)` :

View SolutionA man pushes against a rigid fixed vertical wall. Which of the following is (are) the most accurate statement(s) related to the situation ?
View SolutionA block of mass `m` is placed on a smooth wedge of inclination `theta` & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
View SolutionA block of mass m is placed on a smooth wedge of inclination. The whole system is accelerated horizontally so that block does not slip on the wedge Find the i) Acceleration of the wedge.ii) Force to be applied on the wedge.iii) Force exerted by the wedge on the block .
View SolutionIn arrangement shown below, the thread pulley and spring are all massless and there is no friction anywhere. The system is in equilibrium. If thread connecting `m_(4)` is cut then just after thread is cut :
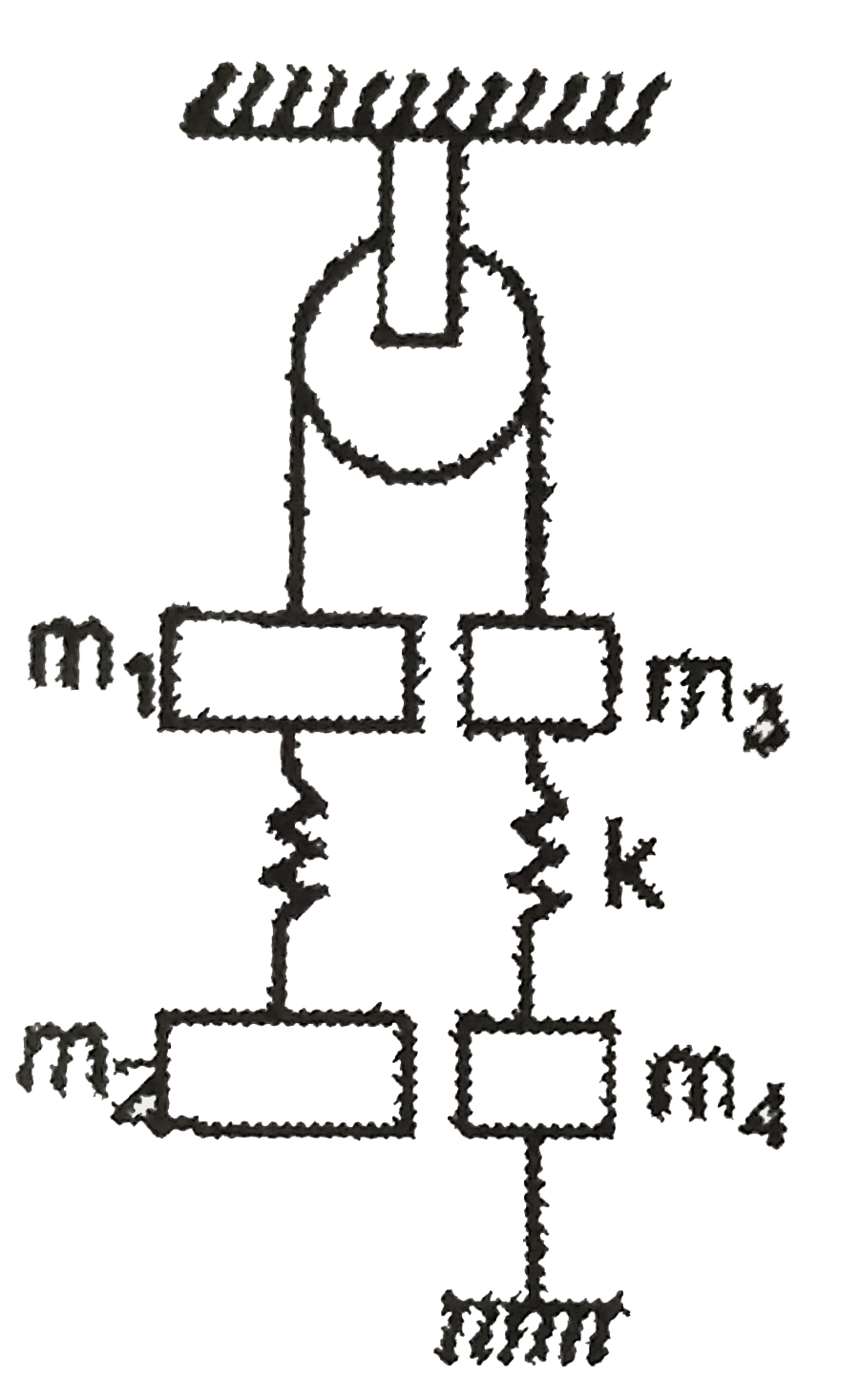
View SolutionA trolley C can run on a smooth horizontal table. Two, much smaller but equal masses A and B are hung by string which pass over smooth pulleys : The string are long enough that when C is in equilibrium. A and B both are just on the ground. The trolley is pulled slow to one side and released as shown below. The graph of its velocity `v` against 't' will be as :

View SolutionIn the system shown in figure `m_(1) gt m_(2)`. System is held at rest by thread BP. Just after the thread BP is burnt :
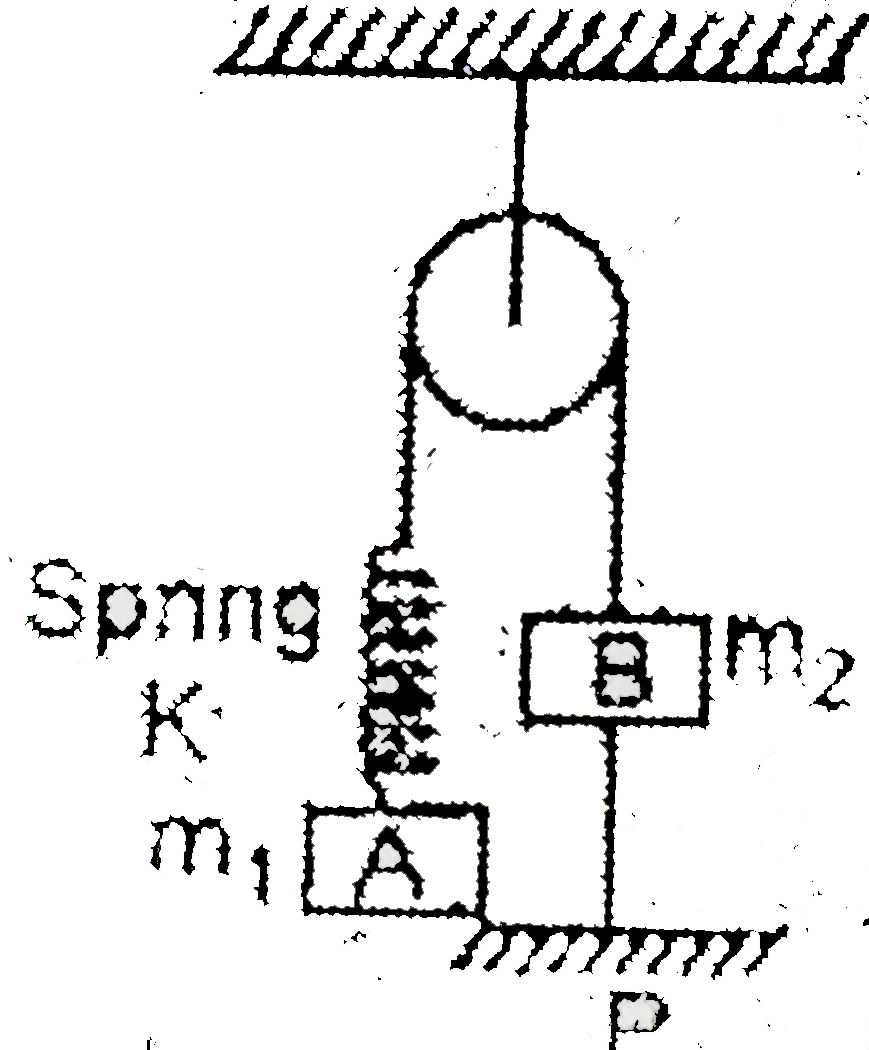
View SolutionA particle is resting over a smooth horizontal floor. At `t=0`, a horizontal force starts acting on it. Magnitude of the force increases with the time according to law `F=at`, where 'a' is a constant. For figure which of the following statement is/are correct ?

View SolutionTwo particle A & B each of mass `m` are in equilibrium in a vertical plane under action of a horizontal force `F=mg` on particle B, as shown in figure Then :

View SolutionThe magnitude of difference in accelerations of block of mass `m` in both the cases shown below is
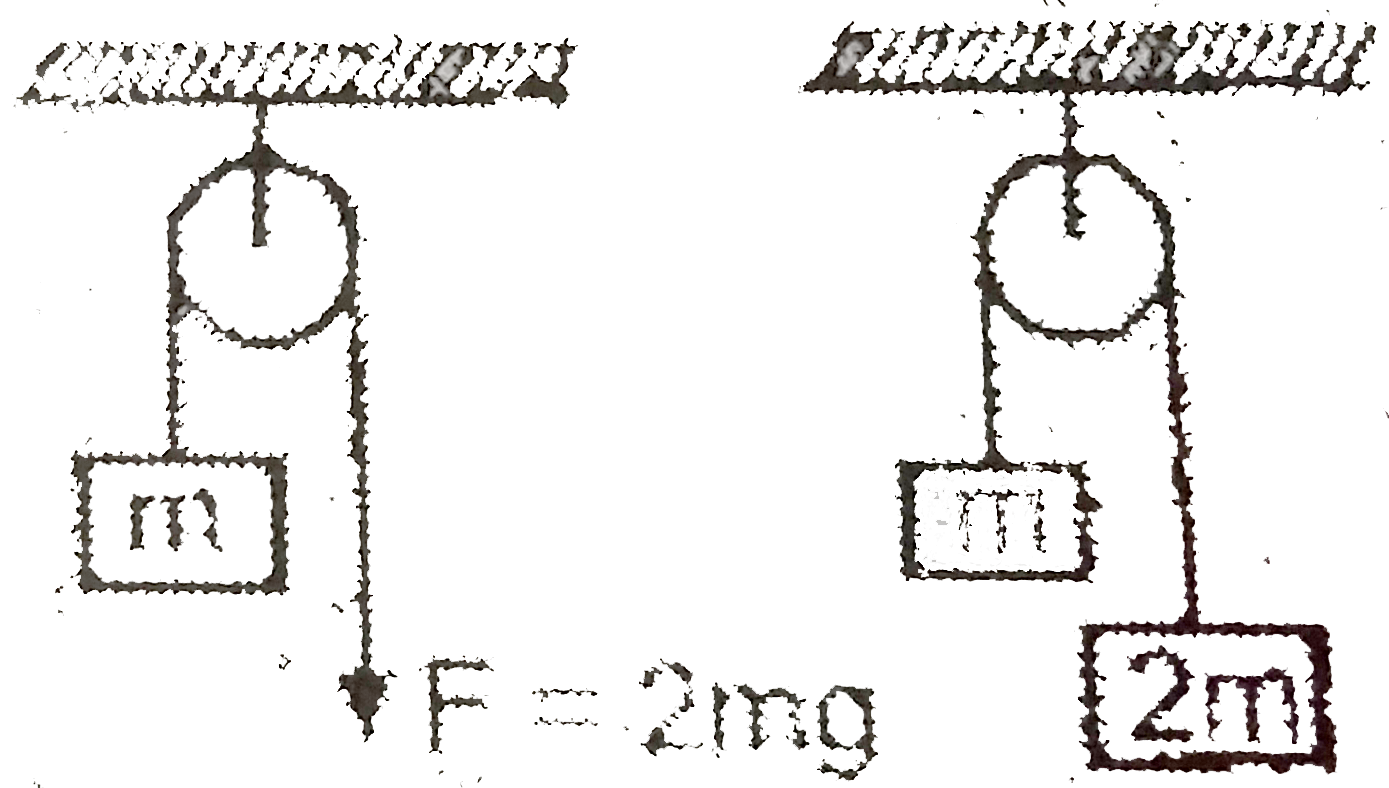
View SolutionIn the figure the block A,B and C of mass `m` each, have acceleration `a_(1),a_(2) & a_(3)` respectively. `F_(1) & F_(2)` are external forces of magnitude 2 mg and mg respectively :
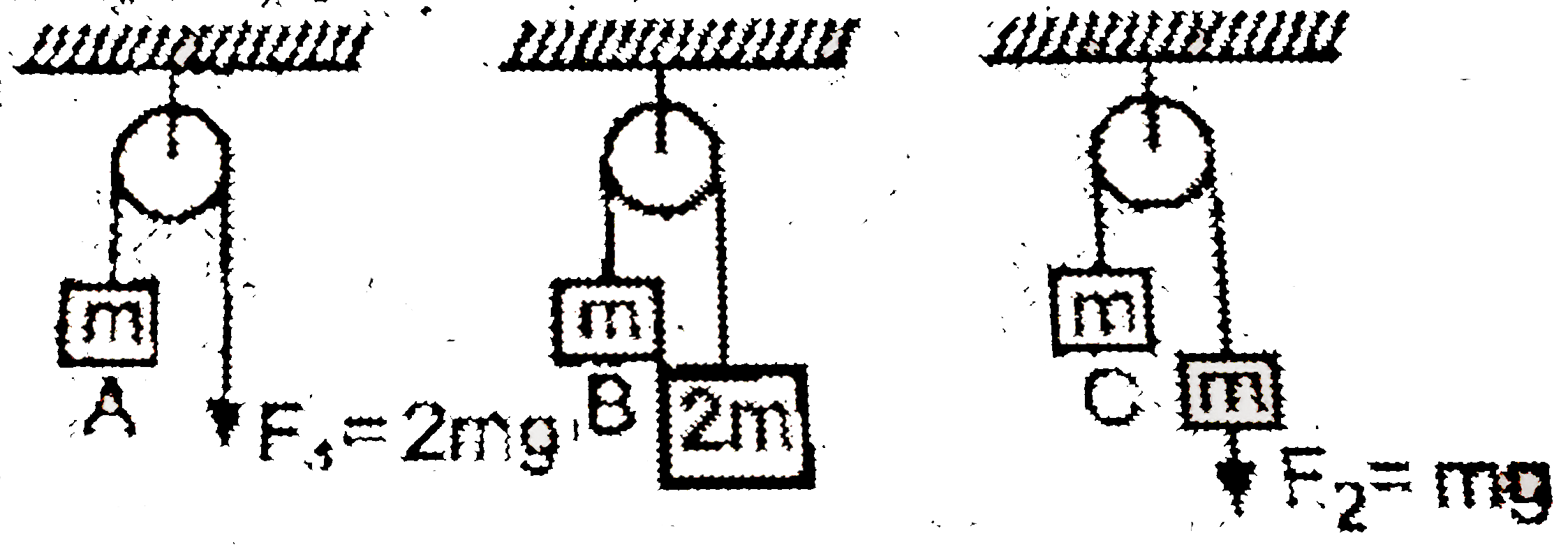
View SolutionA man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in figure. Indicate the correct statements : (assume both the friends apply equal forces of equal magnitude)
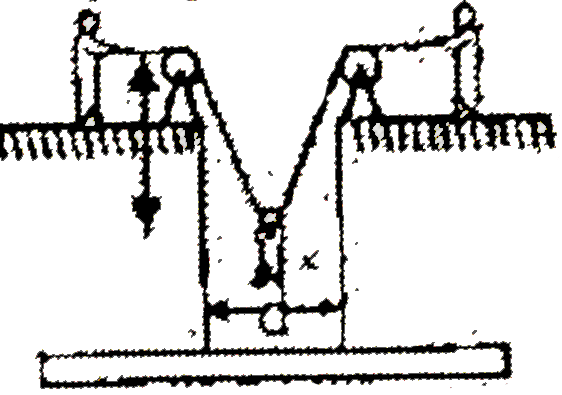
View SolutionIn the figure shown `m_(1)=1 kg,m_(2)=2kg`, pulley is ideal. At `t=0`, both masses touches the ground and string is taut. A force `F=2t` is applied to pulley (t is in second) then `(g = 10 m//s^(2))` :
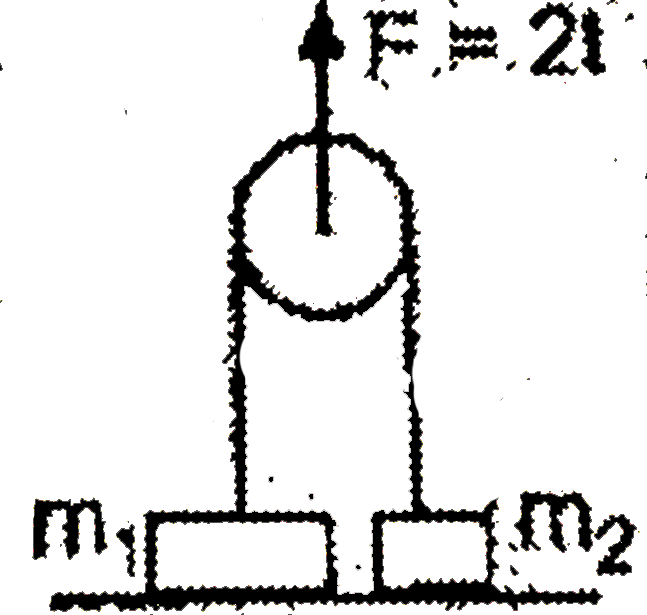
View SolutionIn the following figure all surfaces are smooth. The system is released from rest , then :
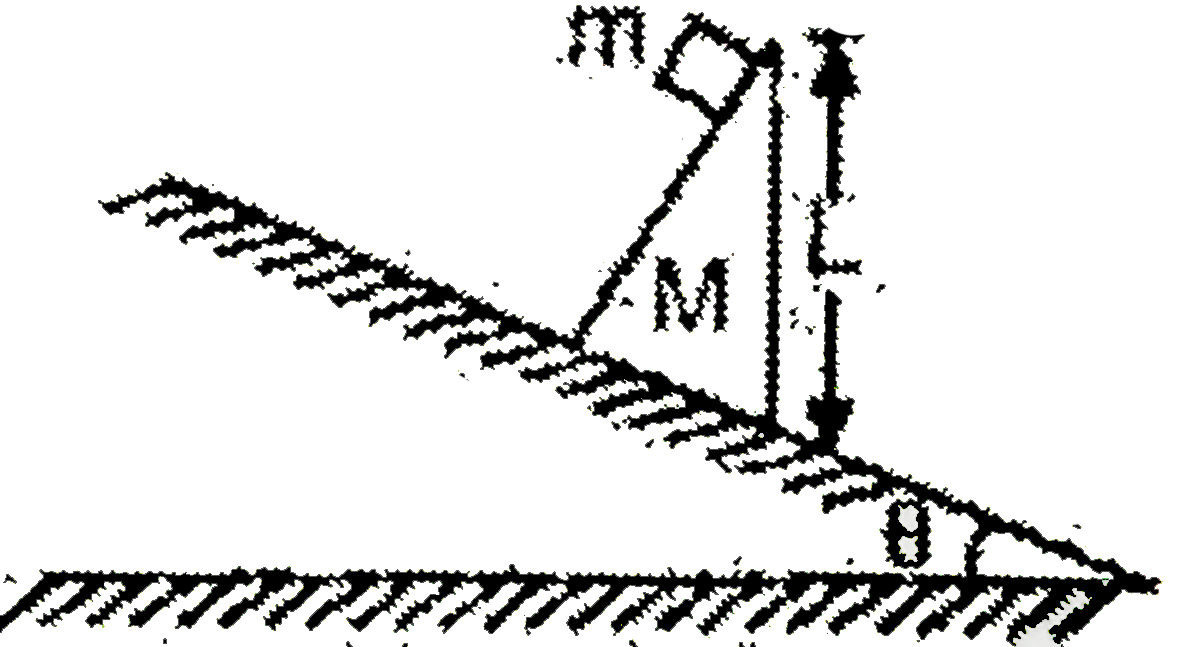
View SolutionThe above question 26, the normal force acting, betweent :
View SolutionIn the figure shown `m_(1)=5 kg,m_(2) = 10 kg` & friction coefficient between `m_(1) & m_(2)` is `mu=0.1` and ground is frictionless then :
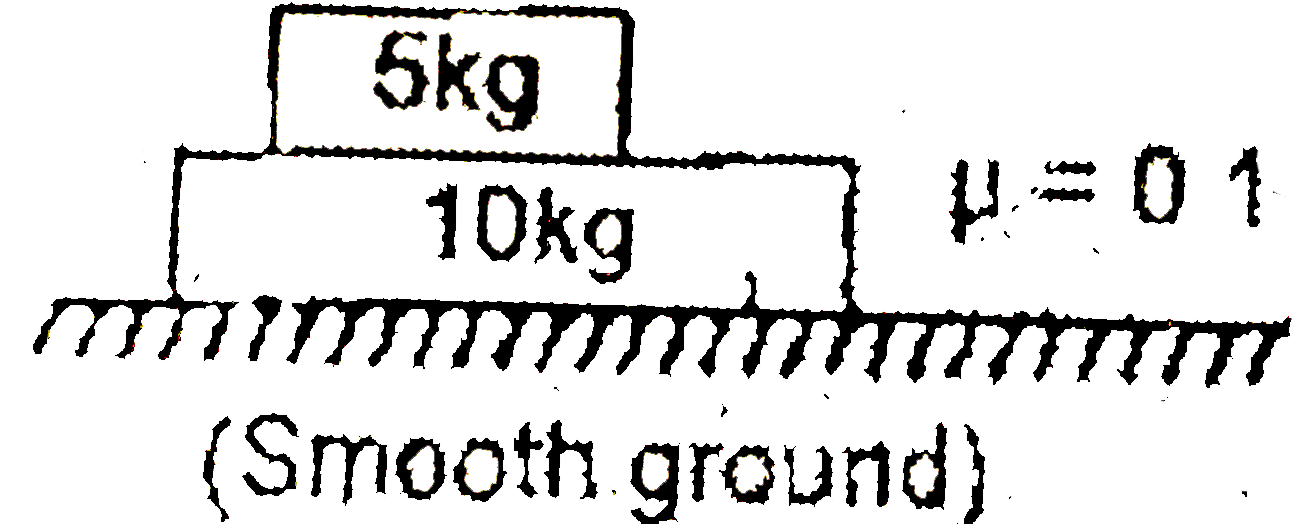
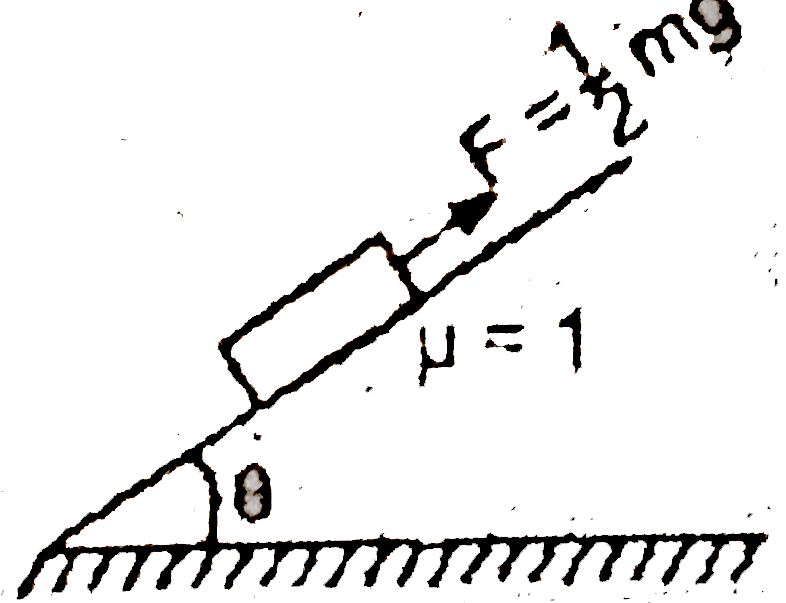
View SolutionA block of mass 0.1 kg is kept on an inclined plane whose angle of inclination can be varied from `theta = 30^(@)` to `theta = 90^(@)`. The coefficient of friction between the block & the inclined plane is `mu =1`. A force of constant magnitude `(1)/(2)mg` newton always acts on the block directed up the inclined plane and parallel to it. Then :
View SolutionIn the situatiobn shown in the figure the friction coefficient between M and the horizontal surface is `mu`. The force F is applied at an angle `theta` with vertical. The correct statements are :

View SolutionIn the arrangement shown, coefficient of friciton for all the surfaces is `mu` and blocks are moving with constant speeds, then :
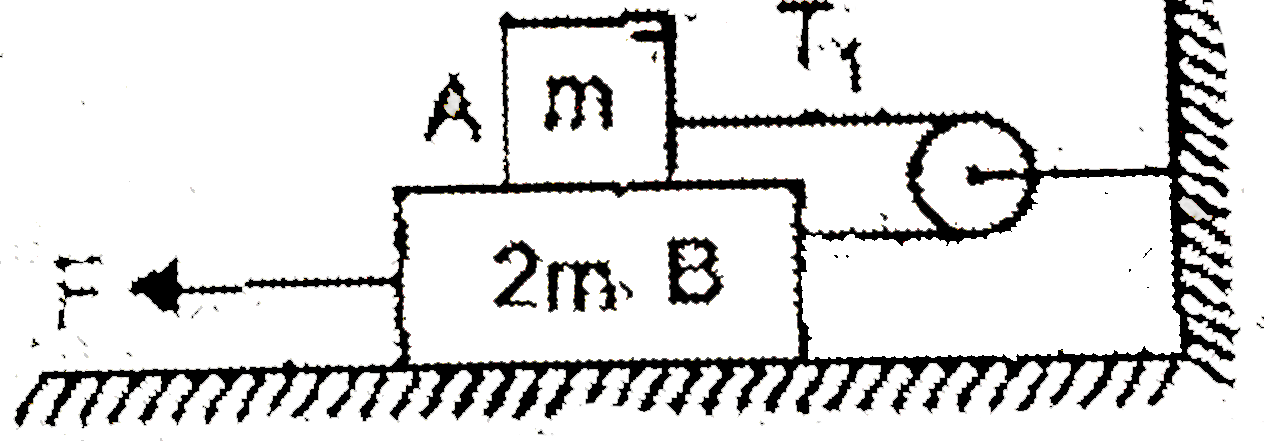
View SolutionA triangular block mass m rests on a fixed rough inclined plane having friction coefficient `mu` with the block. A horizontal force F is applied to it as shown in figure below, then the correct statement is :
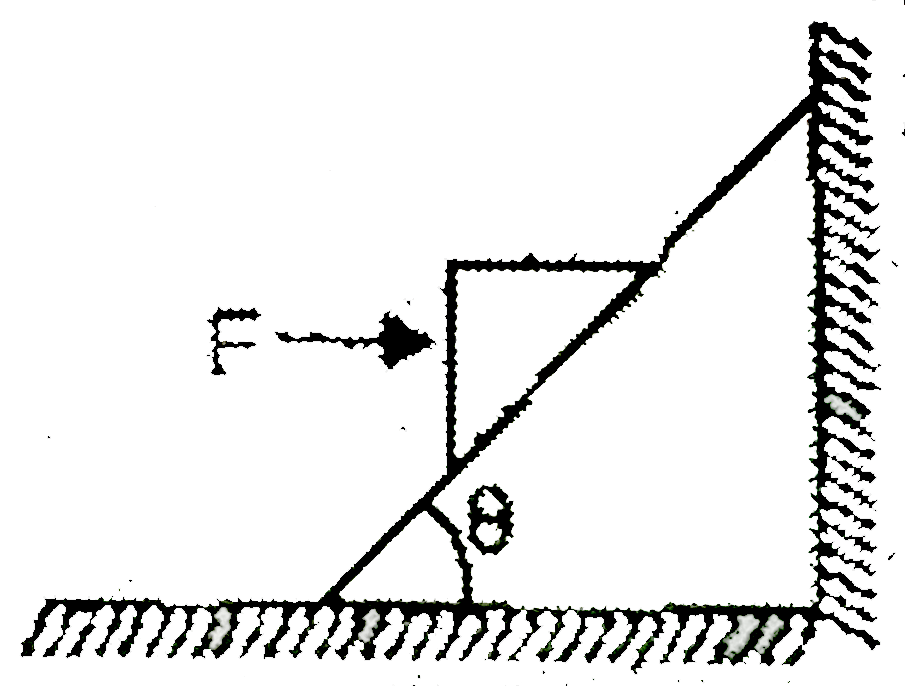
View SolutionA body is moving down a long inclined plane of inclination `45^(@)` with horizontal. The coefficient of friciton between the body and the plane varies as `mu = x//2`, where `x` is the distance moved down the plane. Initially `x=0 & v=0`
View SolutionSuppose `F,F_(N) & f` are the magnitudes of the contact force, normal force and the frictional force exerted by one surface on the other, kept in contact, if none of these is zero :
View SolutionBlock A is placed on block B. There is friction between the blocks, while the ground is smooth. A horizontal force P, increasing linearly with time, begins to act on A. The accelerations `a_(1) & a_(2)` of A and B respectively. Are plotted against time (t). Time correct graph is :

View SolutionIn the shown diagram `m_(1)=m_(2)=4kg` and `m_(3)=2 kg`. Coefficient of friction between `m_(1) and m_(2)` is 0.5. The mass `m_(1)` is given a velocity `v` and it just stops at the other end of the mass `m_(1)` in 1 sec. Let `a_(1) and a_(2) and a_(3)` be the acceleration `m_(1),m_(2)and m_(3)` respectively, then :
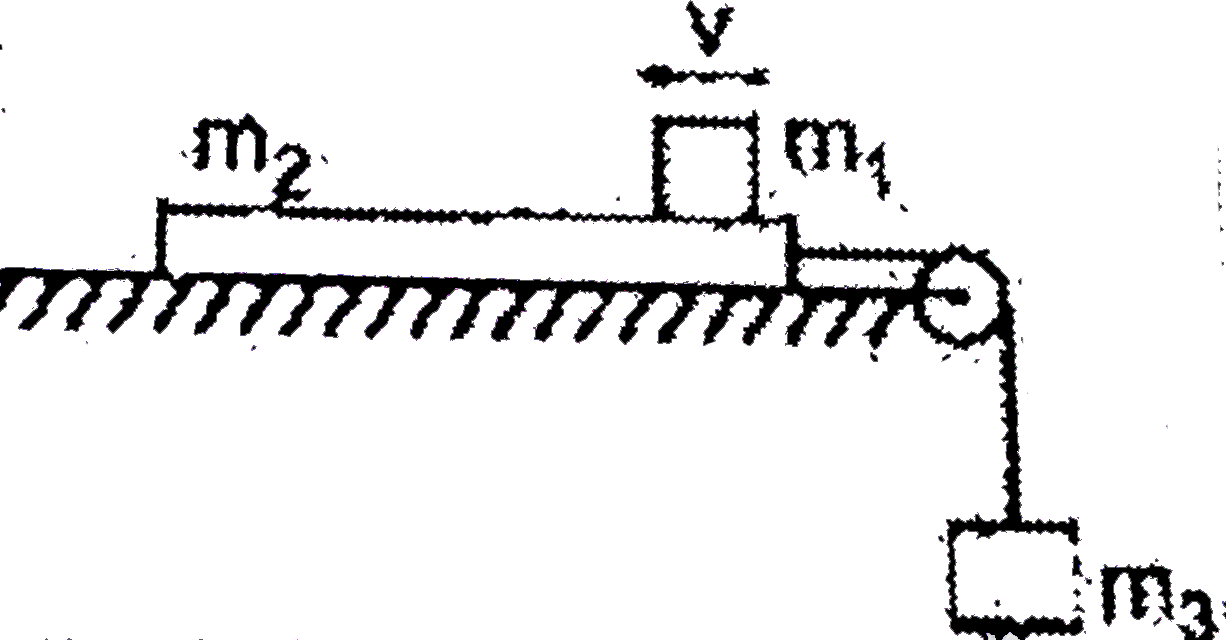
View SolutionO is a point at the bottom of a rough plane inclined at an angle `alpha` to horizontal Coefficient of friciton between AB is `(tan alpha)/(2)` and between BO is `(3 tan alpha)/(2)B` is the middle point of AO, A block if released from rest at A, then which of the following graphs are correct :
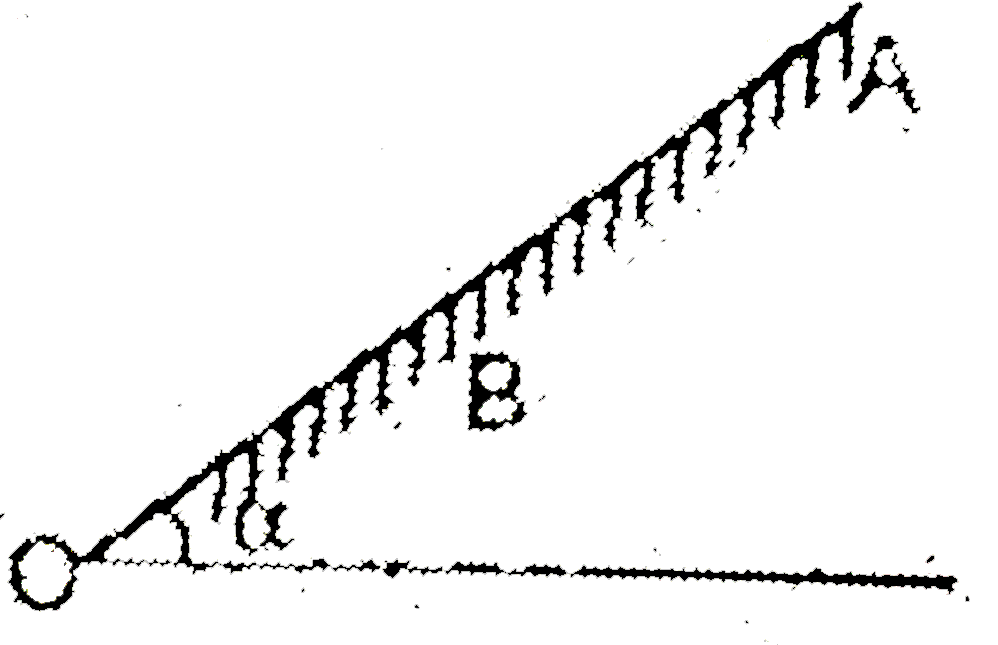
View SolutionIn above question 37 :
View SolutionThe friction coefficient between the plank and floor is `mu`. The man applies, the maximum possible force on the string and the system remains at rest. Then :
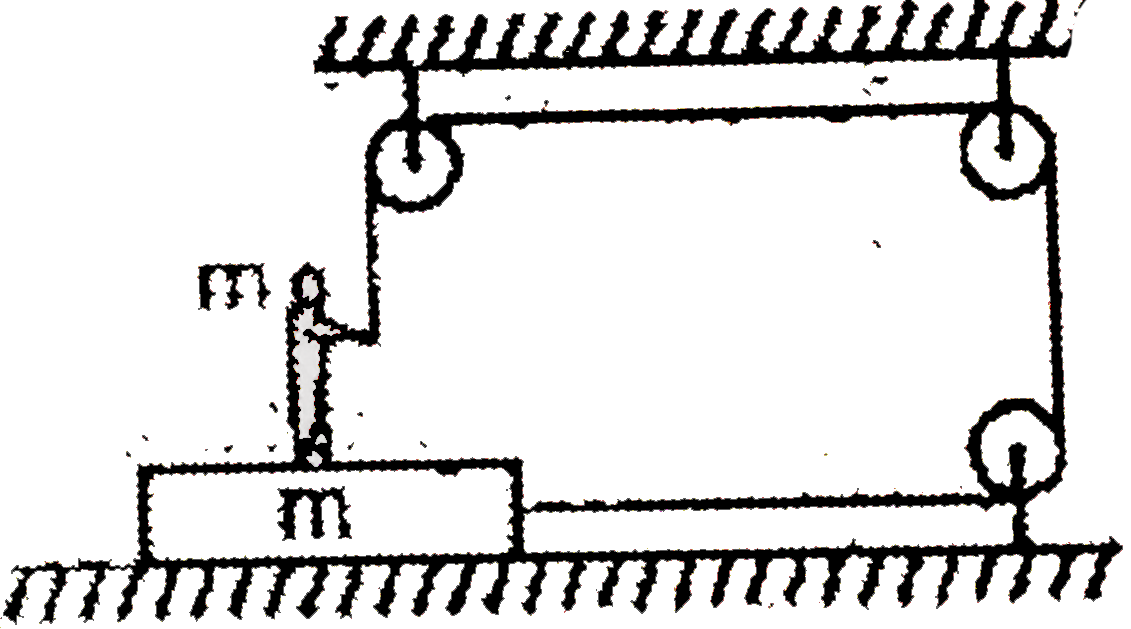
View SolutionIn the figure shown, friction exists between wedge and block and also between wedge and floor. The system is in equilibrium in the shown position.
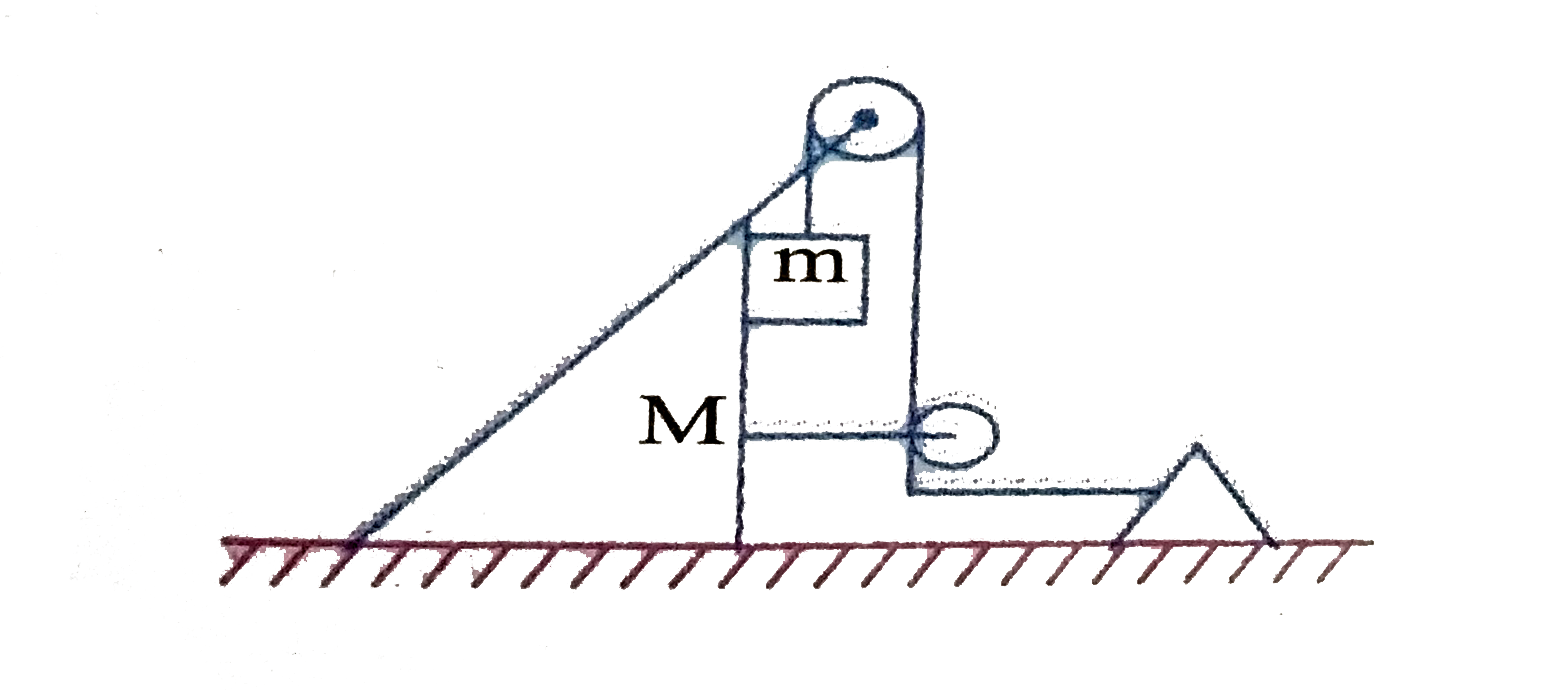
View SolutionA block is projected with velocity `v_(0)` up the inclined plane from its bottom at `t=0`. The plane makes an angle `theta` with the horizontal. If the coefficient of friction between the block and the incline is `mu = tan alpha(alpha gt theta)` then fricitonal force applied by the plane on the block for `t gt (v_(0))/(g[sin theta+tan alpha cos theta])` will be :
View SolutionIn the shown diagram friction exits at each contact surface with coefficient `mu` and the blocks are at rest. Then :
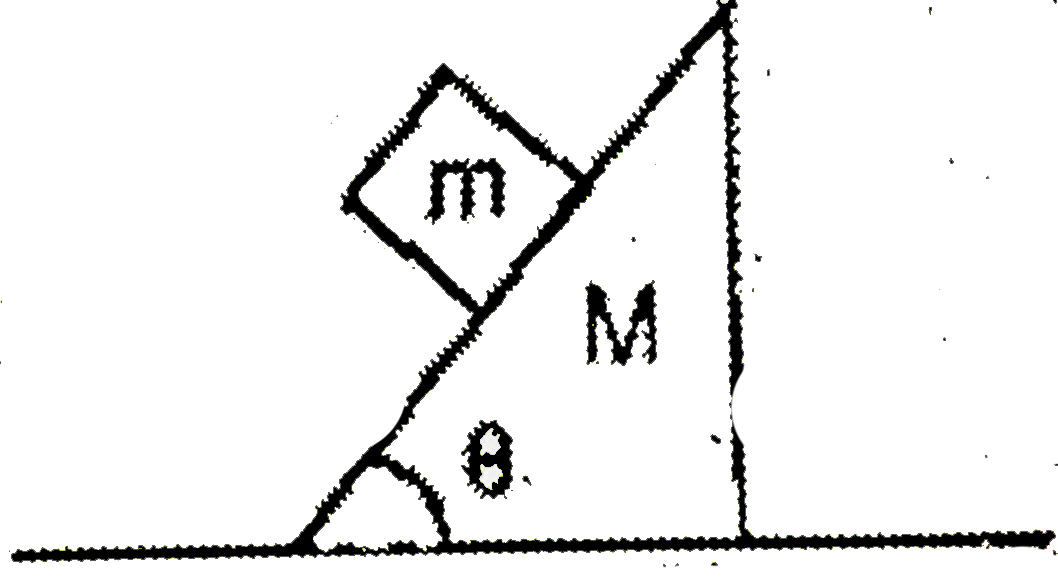
View SolutionA sphere of weight `W = 100 N` is kept stationary on a rough inclined plane by a horizontal string AB as shown in figure. Then :

View SolutionThe position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
View Solution`ABCDE` is a smooth iron track in the vertical plane. The sections `ABC` and `CDE` are quarter circles. Points `B` and `D` are very close to `C.M` is a small magnet of mass `m`. The force of attraction between `M` and the track is `F`, which is constant and always normal to the track. `M` starts from rest at `A`, then:
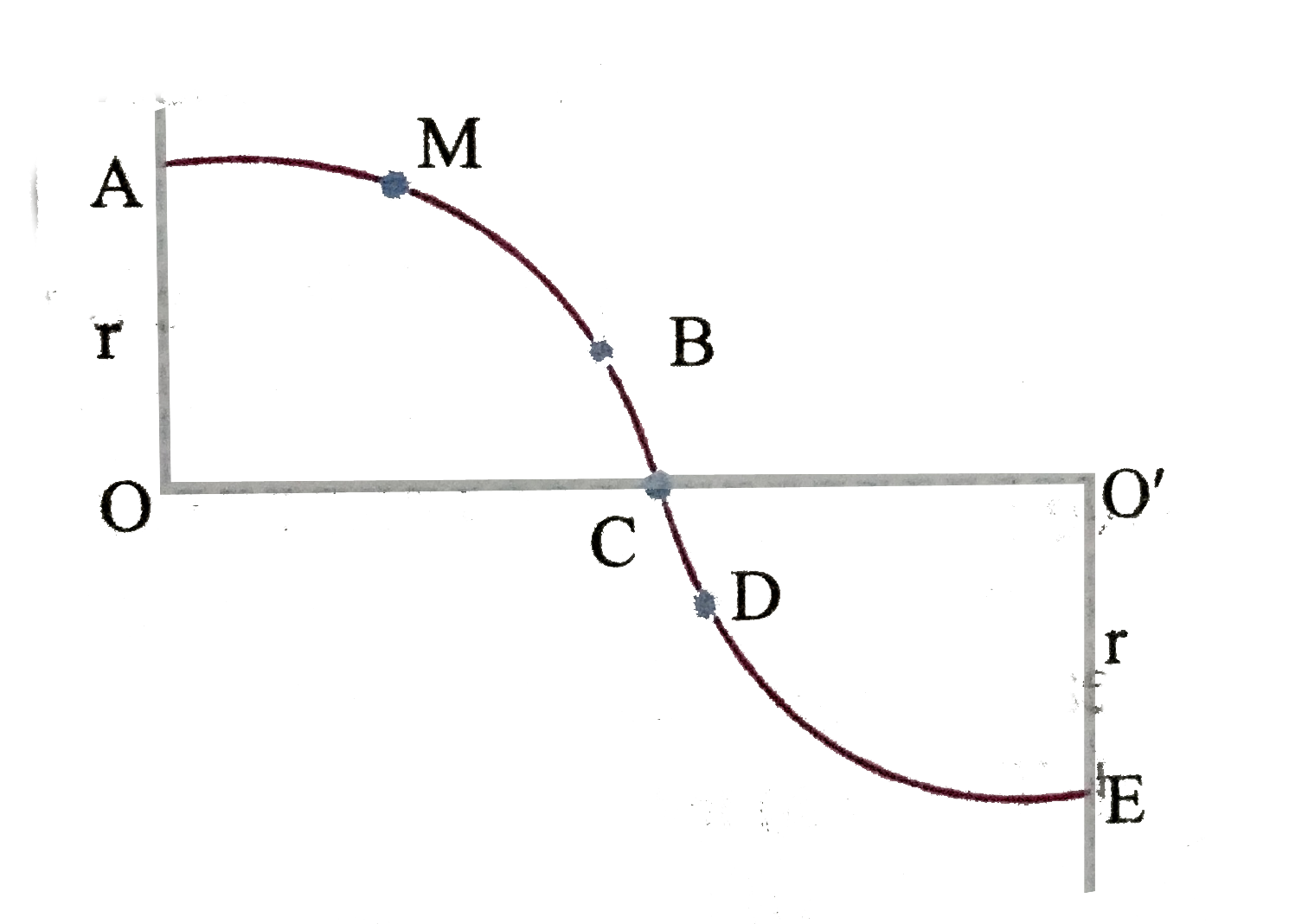
View SolutionA particle is moving along a circular path. The angular velocity, linear velocity, angular acceleration and centripetal acceleration of the particle at any instant are `vec(omega),vec(v),vec(a),vec(a)_(c)` respectively. Which of the following relations are correct ?
View SolutionSuppose a machine consists of a cage at the end of one arm The arm is hinged at O as shown in figure such that the cage revolves along a vertical circle of radius r at constant linear speed `v = sqrt(gr)`. The cage is so attached that the man of weight W, standing on a weighing machine inside the cage, remains always vertical. Then :

View SolutionA smooth circular rod of radius r is banked for a speed `v=40 km//hr`. A car of mass `m` attempts to go on the circular road. The friction coefficient between the type and the road is negligible, The correct statements are :
View SolutionA body moves on a horizontal circular road of radius `r`, with a tangential acceleration `a_(t)`. The coefficient of friction between the body and the road surface Is `mu`. It begins to slip when its speed is `v`.
(i) `v^(2)=murg`
(ii) `mug=(v^(4)/(r^92))+a_(t))`
(iii) `mu^(2)g^(2)=(v^(4)/(r^(2)+a_(t)^(2))`
(iv) The force of friction makes an angle `tan^(-1)(v^(2)//a_(t)r)` with the direction of motion at the point of slipping.
View SolutionA particle `P` of mass `m` is attached to a vertical axis by two strings `AP` and `BP` of legth `l` each. The separation `AB=l`, rotates around the axis with an angular velocity `omega`. The tension in the two string are `T_(1)` and `T_(2)`. Then
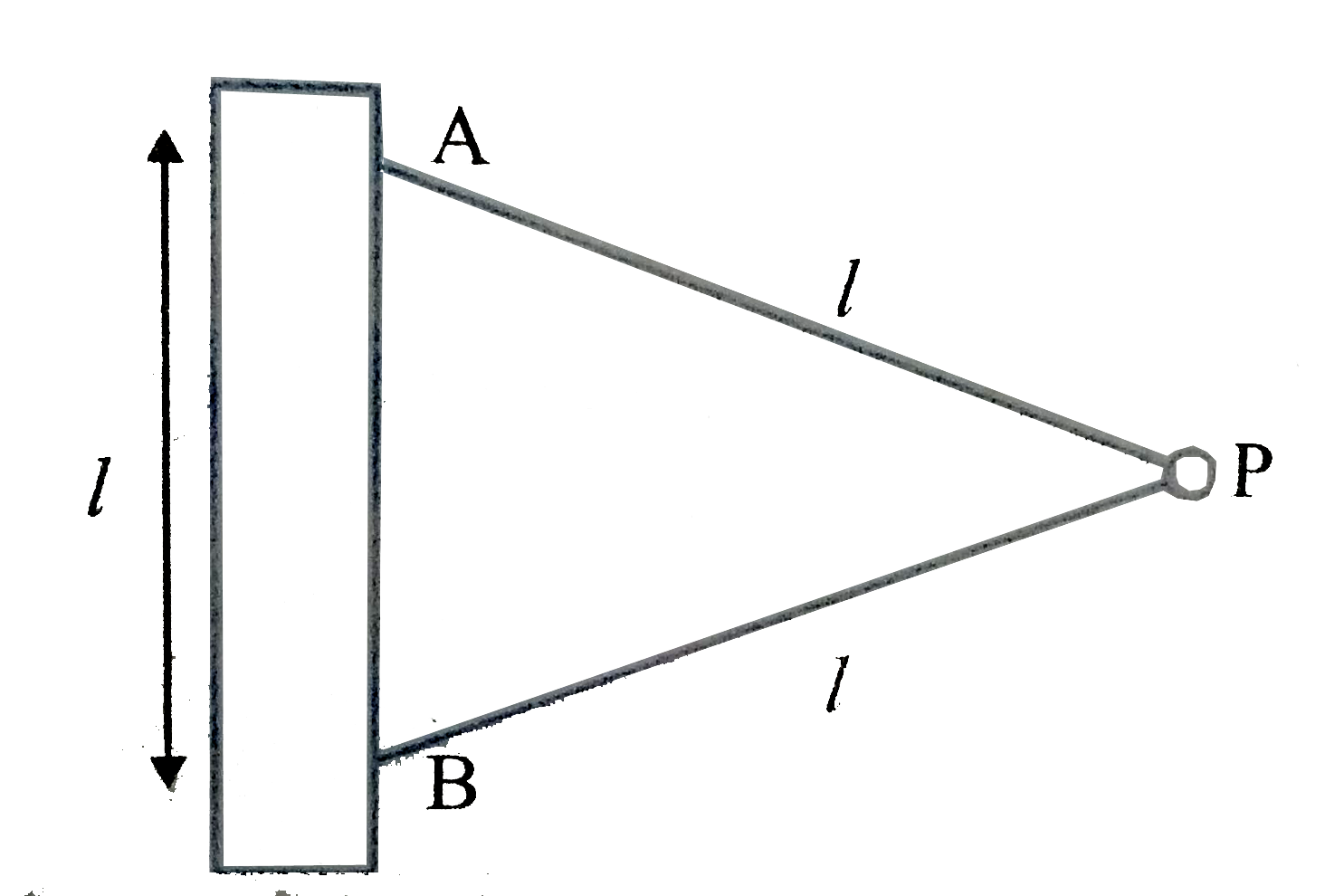
View SolutionAs shown below AB represents an infinite wall tangential to a horizontal semi-circular track. O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with a speed `v` starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively `V` and a, then :

View SolutionA curved section of a road is banked for a speed `v`. If there is no friction between the road and the tyres then.
View SolutionA tube of length 'L' is filled completely with an in compressiblem liquid of mass 'M' and closed at both ends. The tube is then rotated in a horizontal plane about one of it's ends with a uniform angular velocity `'omega'`. Then which of following statements are true :
View SolutionA particle of mass `m` describe circular path of radius 'r' and its radial or normal or centripetal acceleration depends on time 't' as `a_(R) = Kt^(2). K` is `+ve` constant Then :
View SolutionA particle of mass 'm' describes circular path of radius 'r' such that its kinetic energy is given by `K = "as"^(2)`. 's' is the distance travelled, 'a' is constant :
View SolutionThree particles describes circular path of radii `r_(1),r_(2) and r_(3)` with constant speed such that all the particles take same time to complete the revolution. If `omega_(1),omega_(2),omega_(3)` be the angular velocity `v_(1),v_(2),v_(3)` be linear velocities and `a_(1),a_(2),a_(3)` be linear acceleration than :
View SolutionA particle of mass `m` describes a circular path of radius 'r' such that speed `V = alpha sqrt(S)` (S is distance traveled). Then power is proportional to :
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity `'omega'` in free space then :
View SolutionA body moves on a horizontal circular road of radius of r, with a tangential acceleration `a_(T)`. Coefficient of friction between the body and road surface is `mu`. It begin to slip when it's speed is `v`, then :
View SolutionA simple pendulum has a bob of mass `m` and swings with an angular amplitude `phi`. The tension in thread is `T`. At a certain time the string makes an angle `theta` with the vertical `(theta le phi)`
View SolutionA particle of mass `m` moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
View SolutionA particle 'A' moves along a circle of radius R = 50 cm, so that its radius vetor 'r' relative to the point O rotates with the constant angular velocity `omega = 0.4 rad//s`. Then :
View SolutionTwo bodies are moving with constant speed `v` clockwise and are initially diagonally opposite. The particle B now acheives a tangential acceleration of a `m//s^(2)`. Then :
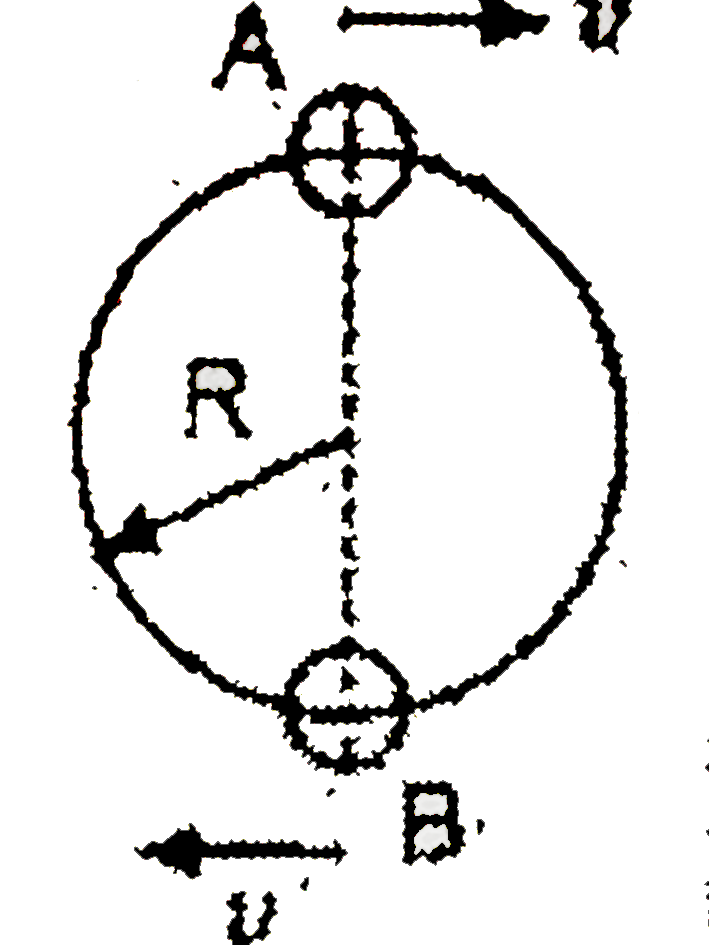
View SolutionA particle P is attached by means of two equal strings to two points A and B is same vertical line and describes horizontal circle with uniform angular speed `2 sqrt((2g)/(h))` where AB = h
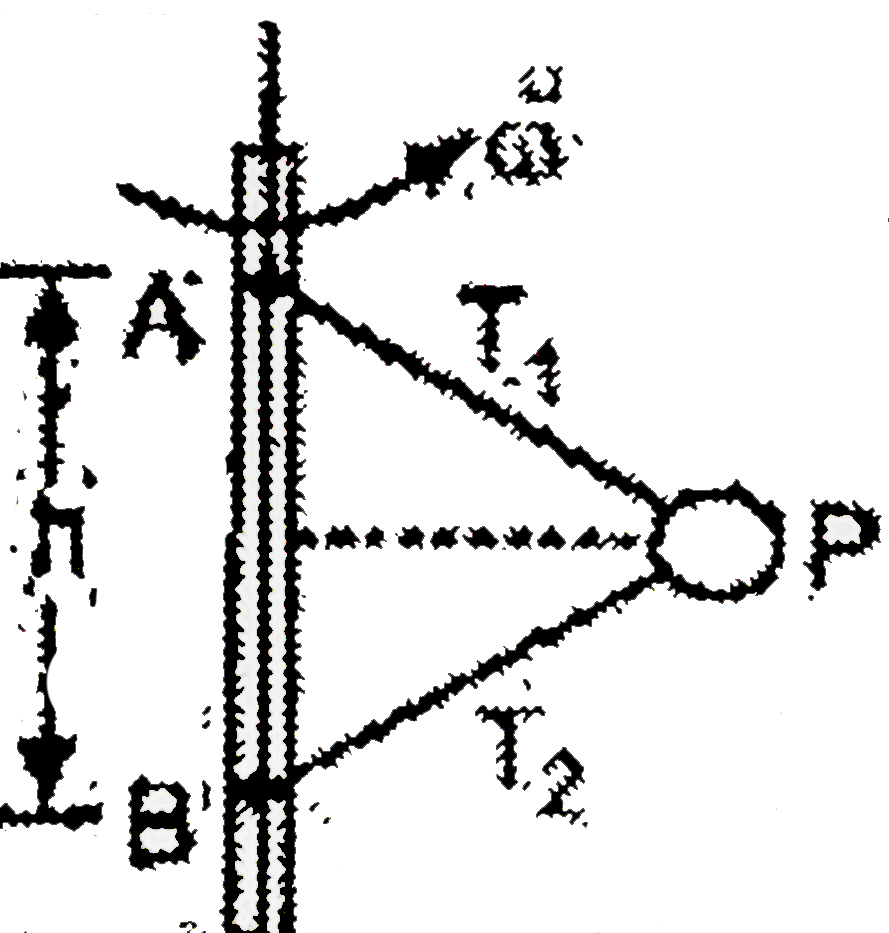
View SolutionA particle is acted upon by constant magnitude force perpendicular to ot which is always perpendicular to velocity of particle. The motion is taking place in a plane it follows that :
View SolutionA particle of mass `m` moves in a conservative force field along `x` axis where the potential energy U varies with position coordinate x as `U = U_(0)(1- cos ax),U_(0)` and a being positive constants. Which of the following statement is true regarding its motion. Its total energy is `U_(0)` and starts from `x=0`
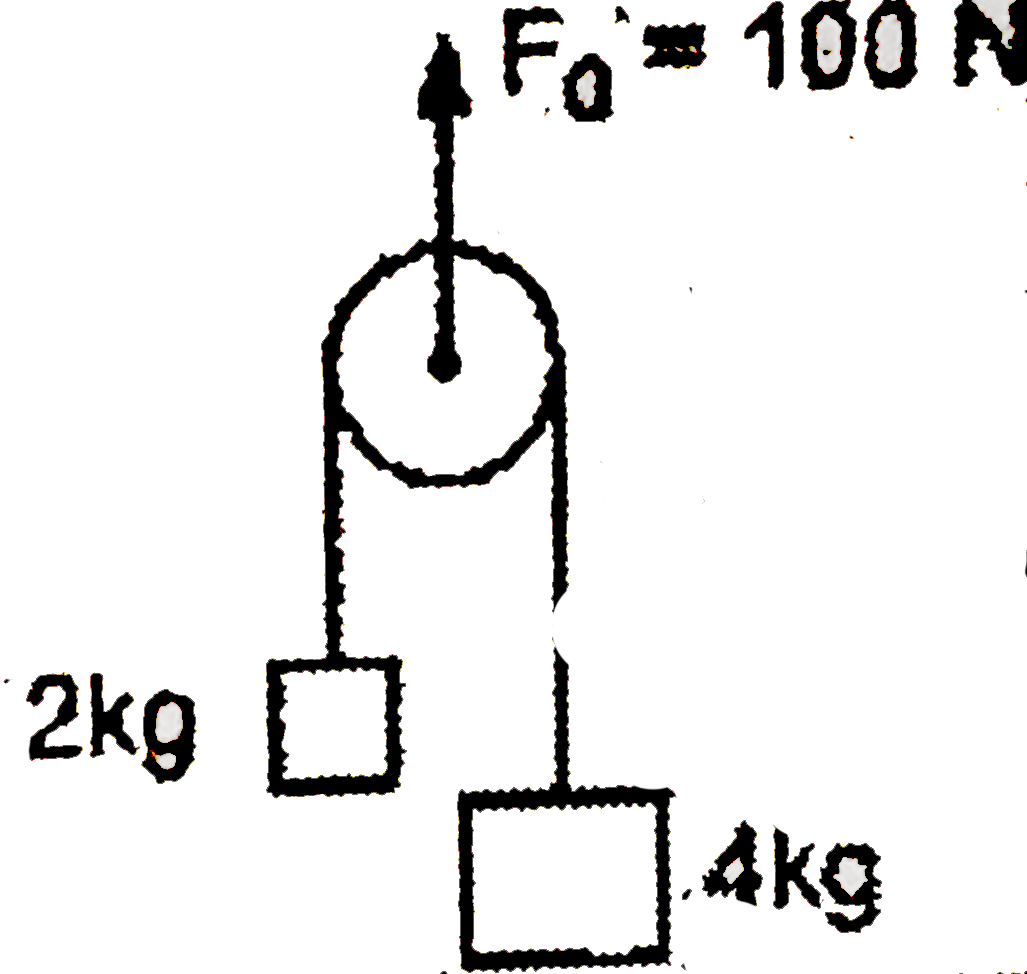
View SolutionTwo blocks of masses `m_(i) = 2kg` and `m_(2) = 4kg` hang, over a massless pulley as shown in the figure. A force `F_(0)=100 N` acting at the axis of the pulley accelerates the system upwards Then :
View SolutionWhich of the following is/are incorrect :
View SolutionA spring block system is placed on a rough horizontal floor. The block is pulled towards right to gives spring some elongation and released, Then :

View SolutionIn the above situation the block will have maximum velocity when :
View SolutionA book leans against a crate on a table. Neither is moving Which of the following statements concerning this situation is/are incorrect.
 .
.
View SolutionAn iron sphere weighing `10N` rests in a `V` shaped smooth trough whose sides form an angle of `60^(@)` as shown in the Then the reaction forces are
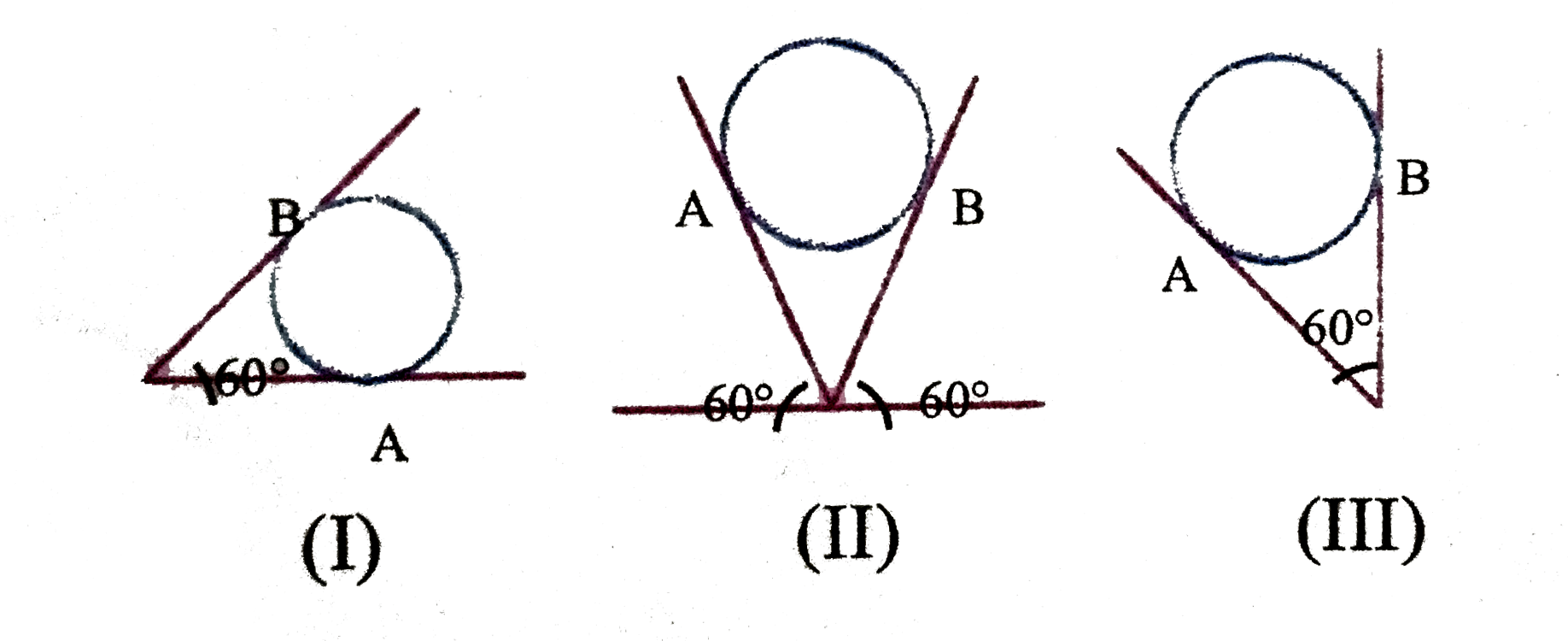 .
.
View SolutionIn the system shown in the figure `m_(1) gt m_(2)`. System is held at rest by thread BC. Just after the thread BC is burnt :
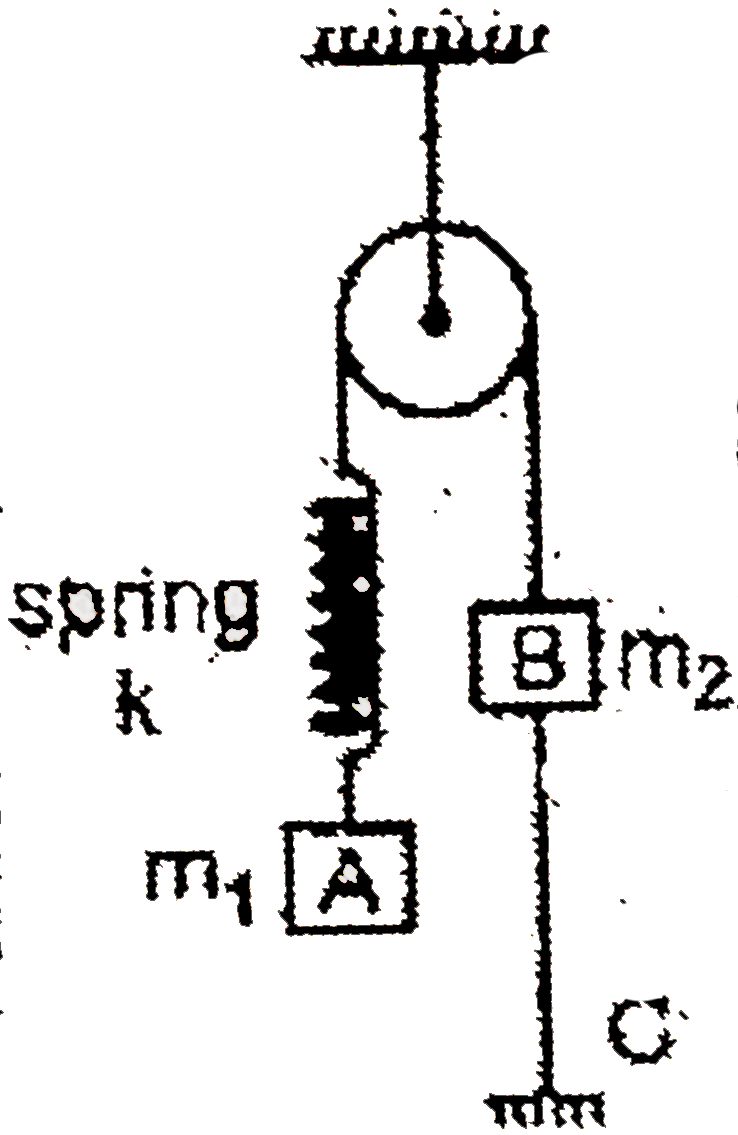
View Solution
Level-2 questions and complete solutions for chapter FORCE ANALYSIS of SHREE BALAJI PHYSICS (HINGLISH) of Class 11