Complete Solutions to Multiple Correct of chapter LINEAR AND ANGULAR SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LINEAR AND ANGULAR SIMPLE HARMONIC MOTION |
| CENGAGE PHYSICS | Multiple Correct |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency `omega`. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionFor a simple harmonic motion with given angular frequency `omega`, two arbitrary initial conditions are necessary and sufficient to determine the motion completely. These initial conditions may be
View SolutionThe potential energy U of a body of unit mass moving in one dimensional conservative force field is given by `U=x^2-4x+3`. All units are is SI. For this situation mark out the correct statement (s).
View Solution
For the spring pendulum shown in fig. the value of spring constant is `3xx10^4(N)/(m)` and amplitude of oscillation is `0.1m`. The total mechanical energy of oscillating system is 200 J. Mark out the correct option (s).
View Solution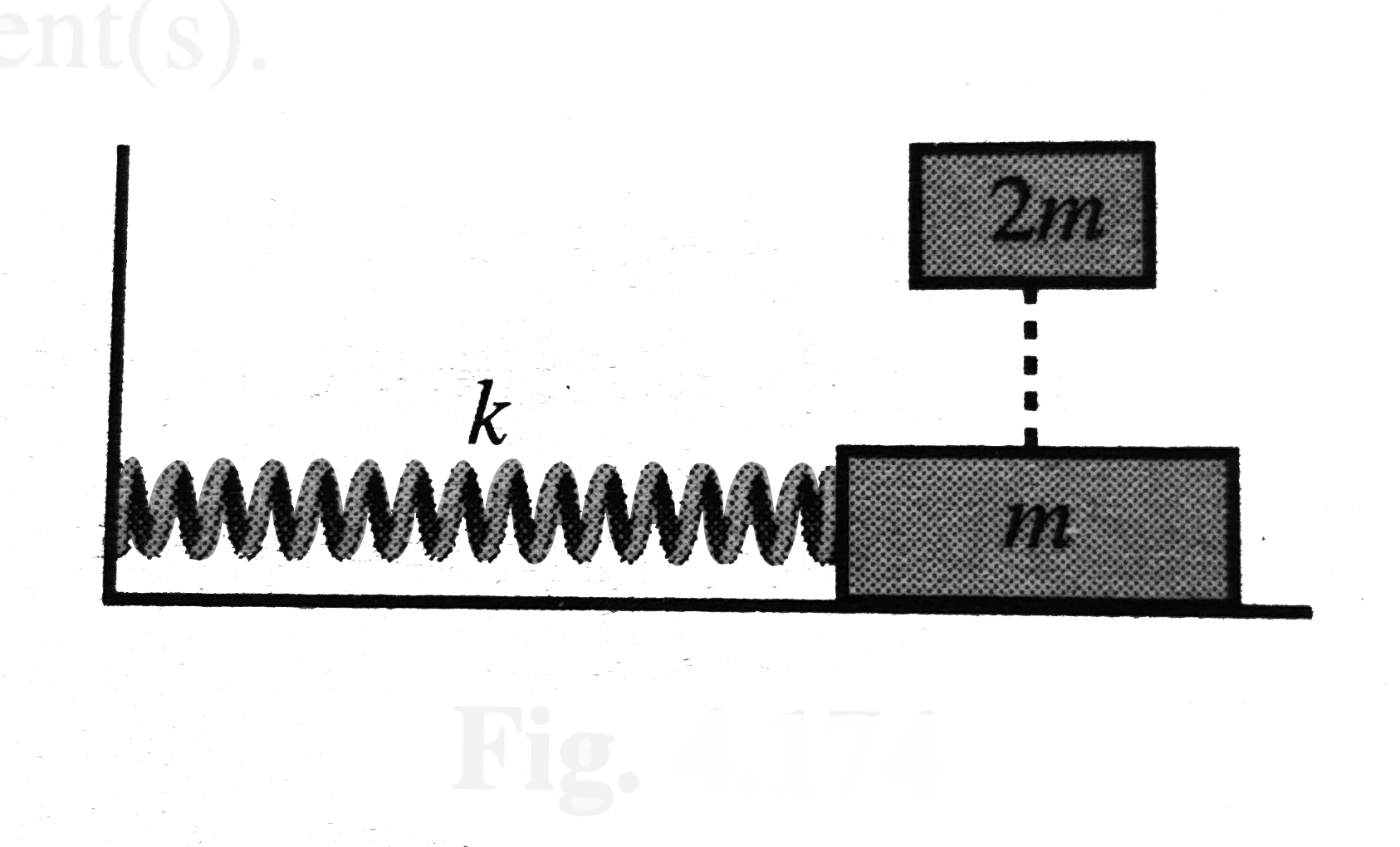
An object of mass m is performing simple harmonic motion on a smooth horizontal surface as shown in Fig. just as the oscillating object reaches its extreme position, another object of mass 2 m is dropped on to oscillating object, which sticks to it. For this situation mark out the correct statement (s).
View Solution
A simple pendulum consists of a bob of mass m and a light string of length l as shown in the fig. another identical ball moving with the small velocity `v_0` collides with the pendulum's bob and sticks to it. For this new pendulum of mass 2 m, mark out the correct statements (s).
View SolutionA particle performing simple harmonic motion undergoes unitial displacement of `(A)/(2)` (where A is the amplitude of simple harmonic motion) in 1 s. At `t=0`, the particle may be at he extreme position or mean position the time period of the simple harmonic motion can be
View SolutionA particle is subjected to two simple harmonic motions along x and y directions according to `x=3sin100pit`, `y=4sin100pit`.
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by `v^2=108-9x^2` (all equation are in CGS units):
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View SolutionA 20g particle is subjected to two simple harmonic motions `x_1=2sin10t`,`x_2=4sin(10t+(pi)/(3))`. Where `x_1` and `x_2` are in metres and t is in seconds.
View Solution
A spring block system undergoes SHM on a smooth horizontal surface, the block is now given some charge and a uniform horizontal electric field E is switched on as shown in Fig. As a result
View SolutionThe potential energt of a particle of mass 0.1 kg, moving along the x-axis, is given by `U=5x(x-4)J`, where x is in meter. It can be concluded that
View SolutionThe time period of a particle in simple harmonic motion is T. Assume potential energy at mean position to be zero. After a time of `(T)/(6)` it passes its mean position its,
View Solution
Figure. (a) shows a spring of force constant k fixed at one end and carrying a mass m at the other end placed on a horizontal frictionless surface. The spring is stretched by a force F. Figure. (b) shows the same spring with both endsf free and a mass m fixed at each free end Each of the spring is streched by the same force F. The mass in case (a) and the masses in case (b) are then released. Which of the following statements are true?
View SolutionWhen the point of suspendion of pendulum is moved, its period of oscillation
View SolutionThe displacement time relation for a particle can be expressed as `y=0.5[cos^2(npit)-sin^2(npit)]` This relation shows that
View SolutionAt two particular closest instant of time `t_1` and `t_2` the displacements of a particle performing SHM are equal. At these instant
View Solution
Two blocks connected by a spring rest on a smooth horizontal plane as shown in Fig. A constant force `F` start acting on block `m_2` as shown in the figure. Which of the following statements are not correct?
View SolutionA block of mass `m` is suspended by a rubber cord of natural length `l=(mg)/(k)`, where k is force constant of the cord. The block is lifted upwards so that the cord becomes just tight and then block is released suddently. Which of the following will not be true?
View SolutionThe displacement (x) of a particle as a function of time (t) is given by
`x=asin(bt+c)`
Where a,b and c are constant of motion. Choose the correct statemetns from the following.
View SolutionA simple pendulum is oscillating between extreme position P and Q about the mean position O. Wchi of the following statements are true about the motion of pendulum?
View Solution
A cylinderical block of density d stays fully immersed in a beaker filled with two immiscible liquids of different densities `d_1` and `d_2` The block is in equilibrium with half of it in liquid 1 and the other half in liquid 2 as shown in the Fig. If the block is given a displacement downwards released, then neglecting friction study the following statements.
View SolutionA mass of 0.2 hg is attached to the lower end of a massles spring of force constant `200(N)/(m)` the opper end of which is fixed to a rigid support. Study the following statements.
View SolutionA spring of spring constant k stores 5 J of energy when stretched by 25 cm. It is kept vertical with one end fixed. A mass m is attached to the other end. It maskes 5 Oscillation per second. Then
View SolutionA particle is subjected to SHM as given by equation `x_1=Asinomegat` and `x_2=A_2sin(omegat+(pi)/(3))`. The maximum acceleration and amplitude of the resultant motion are `a_(max)` and `A`, respectively Then.
View SolutionThree simple harmonic motions in the same direction each of amplitude `a` and periodic time `T`, are superposed. The first and second and the second and third differ in phase from each other by `(pi)/(4)`, with the first and third not being identical . Then.
View Solution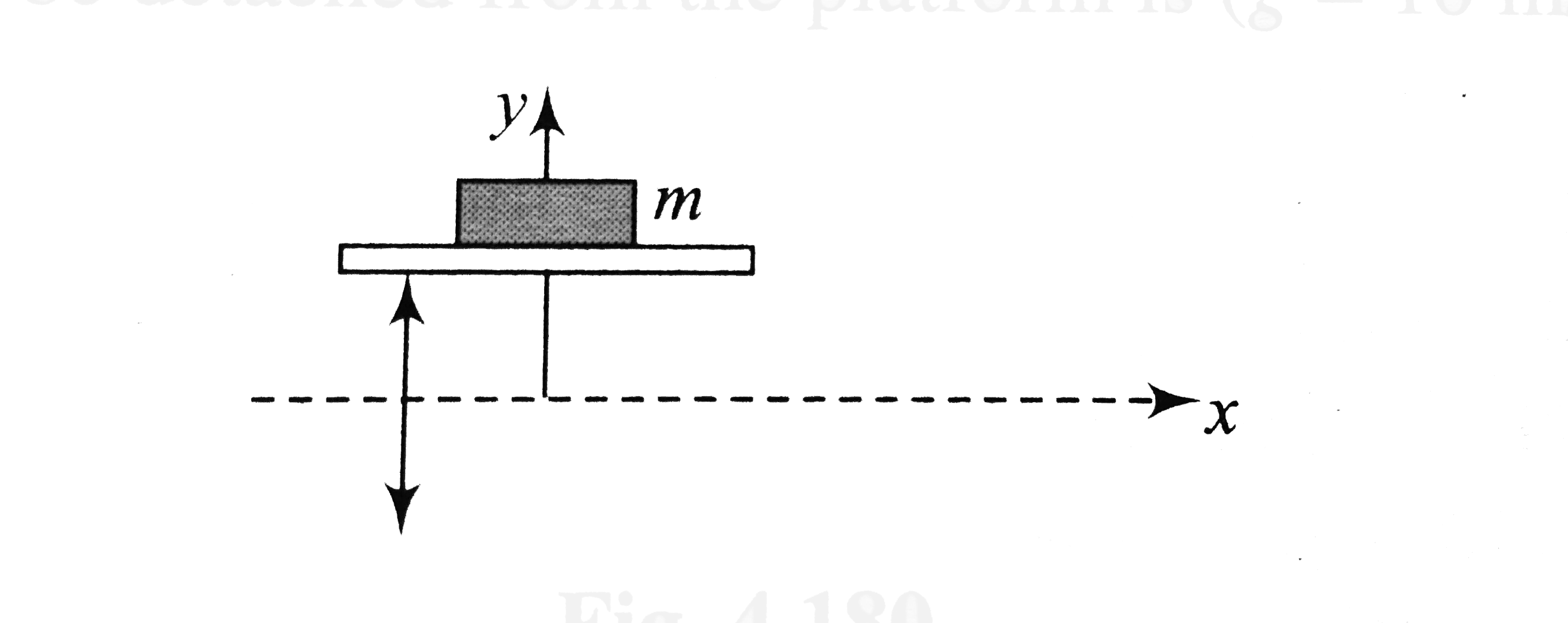
A horizontal platform with a mass `m` placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform `(g=10(m)/(s^2)`)
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by `v^2=108-9x^2` (all equation are in CGS units):
View SolutionFor a body executing SHM with amplitude A, time period T, maximum velocity `v_(max)` and phace constant zero, which of the following statements are correct for `0letle(T)/(4)` (y is displacement from mean position)?
View SolutionIf y, v and a represent displacement velocity and acceleration at any instant for a particle executing SHM, which of the following statements are true?
View SolutionThe time period of a particle in simple harmonic motion is T. Assume potential energy at mean position to be zero. After a time of `(T)/(6)` it passes its mean position its,
View SolutionThe potential energt of a particle of mass 0.1 kg, moving along the x-axis, is given by `U=5x(x-4)J`, where x is in meter. It can be concluded that
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View SolutionA particle moves in the X-Y plane according to the equation `vecr=(veci+2vecj)Acosomegat`. The motion of the particle is
View Solution
Multiple Correct questions and complete solutions for chapter LINEAR AND ANGULAR SIMPLE HARMONIC MOTION of CENGAGE PHYSICS (HINGLISH) of Class 11