Complete Solutions to Single Correct of chapter LINEAR AND ANGULAR SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LINEAR AND ANGULAR SIMPLE HARMONIC MOTION |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
While a particle executes linear simple harmonic motion
View SolutionWhile a particle executes simple harmonic motion, the rate of change of acceleration is maximum and minimum respectively at
View SolutionA hollow sphere filled with water through a small body in it is then hung by a long thread and made to oscillation As the water slowly force end of the hole at the bottom the period of oscillation will
View SolutionA simple pendulum oscillates slightly above a large horizontal metal plate. The bob is given a charge. The time period
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of `2.0s` in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionThe number of independent constituent simple harmonic motions yielding a resultant displacement equation of the periodic motion as `y=8sin^2((t)/(2))sin(10t)` is
View Solution
The diagram below shows a sinusoidal curve. The equation of the curve will be
View Solution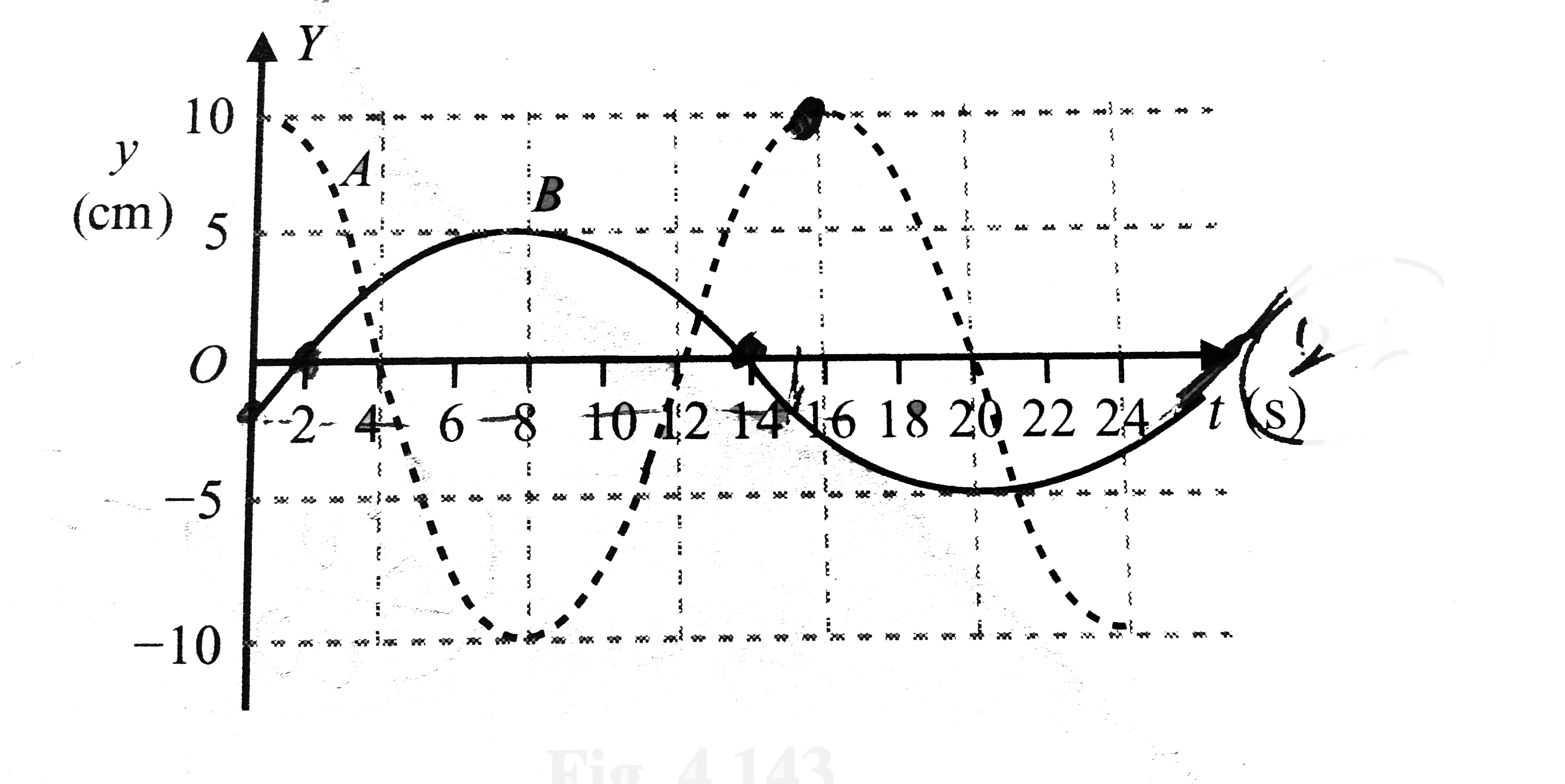
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is
View Solution
The variation of velocity of a particle executing SHM with time is shown is fig. The velocity of the particle when a phase change of `(pi)/(6)` takes place from the instant it is at one of the extreme positions will be
View SolutionIn the previous problem, the displacement of the particle from the mean position corresponding to the instant mentioned is
View SolutionIn problem 9 , the acceleration of the particle is
View SolutionIn problem 9 the acceleration of the particle is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View SolutionA block of mass `1kg` hangs without vibrating at the end of a spring whose force constant is `200(N)/(m)` and which is attached to the ceiling of an elevator. The elevator is rising with an upward acceleration of `(g)/(3)` when the acceleration suddenly ceases. The angular frequency of the block after the acceleration ceases is
View SolutionA vertical spring carries a `5kg` body and is hanging in equilibrium an additional force is applied so that the spring is further stretched. When released from this position. It performs 50 complete oscillation in 25 s, with an amplitude of 5 cm. The additional force applied is
View SolutionA particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the SHM is
View SolutionA particle free to move along the (x - axis) hsd potential energy given by `U(x)= k[1 - exp(-x^2)] for -o o le x le + o o`, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionTwo simple harmonic motion are represented by equations
`y_(1) = 4 sin (10 t + phi)` and `y_(2) = 5 cos 10t`
What is the phase difference between their velocities ?
View SolutionThe metallic bob of a simple pendulum has the relative density `rho`. The time period of this pendulum is `T` if the metallic bob is immersed in water the new time period is given by
View SolutionTwo particles move parallel to x - axis about the origin with the same amplitude and frequency. At a certain instant they are found at distance `(A)/(3)` from the origin on opposite sides but their velocities are found to be in the same direction. What is the phase difference between the two ?
View SolutionThe potential energy of a particle executing SHM along the x-axis is given by `U=U_0-U_0cosax`. What is the period of oscillation?
View SolutionA particle executing SHM of amplitude `a` has displacement `(a)/(2)` at `t=(T)/(4)` and a negative velocity. The epoch of the particle is
View SolutionA block of mass 4 kg hangs from a spring constant `k=400(N)/(m)`. The block is pulled down through 15 cm below and released. What is its kinetic energy when the block is 10 above the equilibrium position.?
View SolutionA body of mass 100 g attached to a spring executed SHM of period 2 s and amplitude 10 cm. How long a time is required for it to move from a point 5 cm below its equilibrium position to a point 5 cm above it, when it makes simple harmonic vertical oscillation (take `g=10(m)/(s^2)`)?
View SolutionA particle executing SHM has velocities `u` and `v`` and acceleration `a` and `b` in two of its position. Find the distance between these two positions.
View SolutionTwo particles are executing identical simple harmonic motions described by the equations `x_1=acos(omegat+((pi)/(6)))` and `x_2=acos(omegat+(pi)/(3)`). The minimum interval of time between the particles crossing the respective mean positions is `(pi)/(2omega)`
View SolutionThe `KE` and `PE` , at is a particle executing `SHM` with amplitude `A` will be equal when its displacement is
View SolutionA body is performing simple harmonic motion with amplitude a and line period `T` variation of its acceleration `(f)` with time`(t)` is shown in figure If a line `x` velocity of the body is `x` which of the following graph is correct?
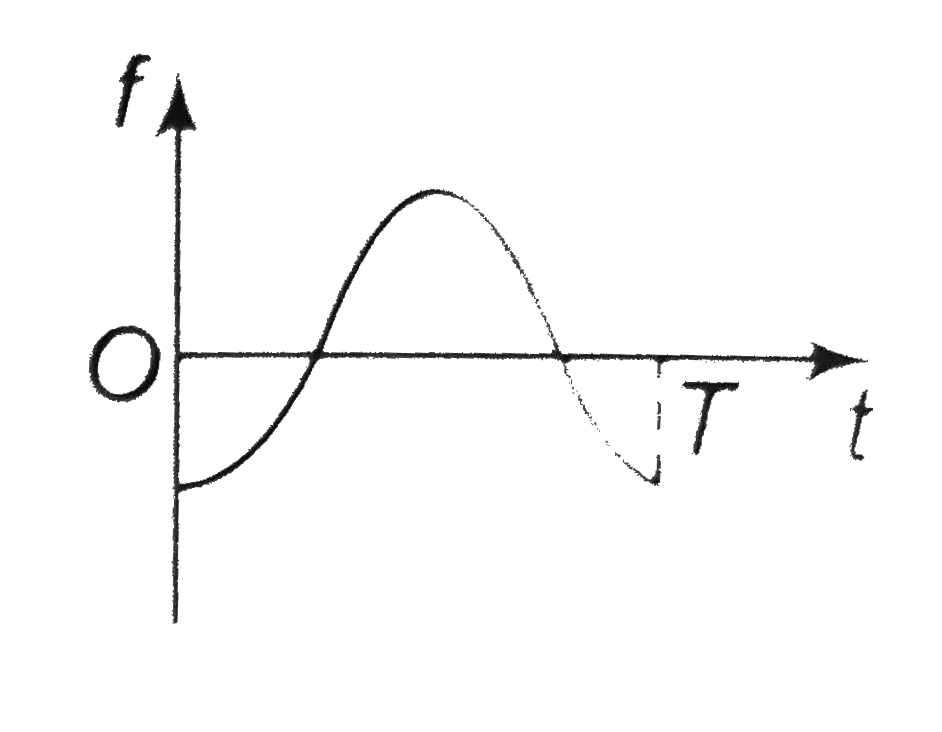
View SolutionA body is performing simple harmonic motion with amplitude a and line period `T` variation of its acceleration `(f)` with time`(t)` is shown in figure If a line `x` velocity of the body is `x` which of the following graph is correct?

View Solution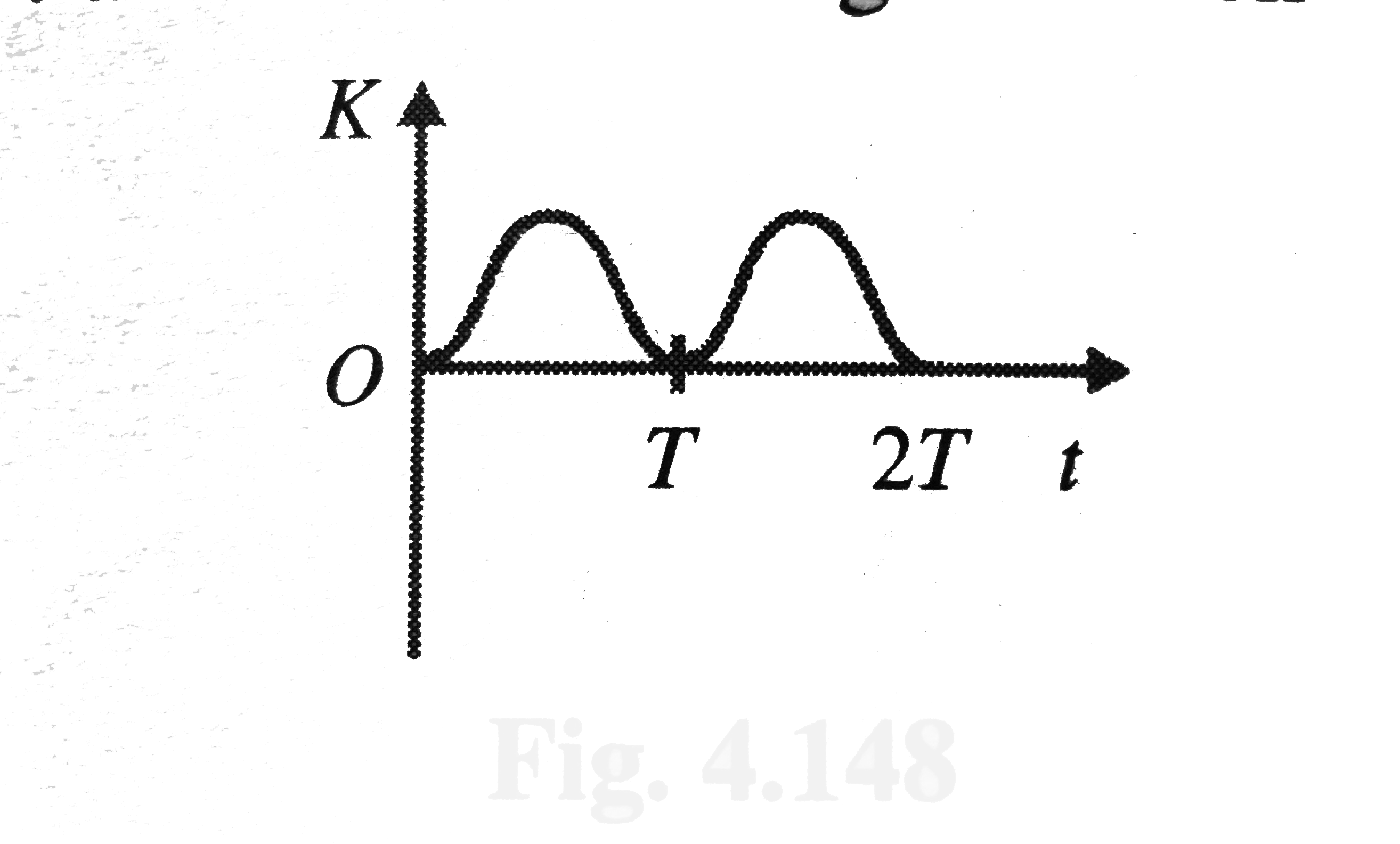
A particle is performing SHM. Its kinetic energy K varies with time t as shown in the figure. Then
View SolutionTwo particle `P` and `Q` describe `S.H.M.` of same amplitude a same frequency `f` along the same straight line .The maximum distance between the two particles is `asqrt(2)` The phase difference between the two particle is
View SolutionTwo masses (m_1) and (m_2) are suspended together by a massless spring of spring constant (k). When the masses are in equilibrium, (m_1) is removed without disturbing the system. Find the angular frequency and amplitude of oscillation of (m_2).
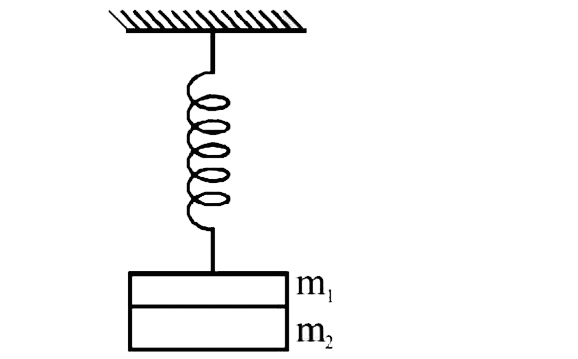 .
.
View SolutionA body of mass `m` is released from a height h to a scale pan hung from a spring. The spring constant of the spring is `k`, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionFrequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is `(g=10(m)/(s))`
View SolutionThe potential energy of a particle of mass `1kg` in motion along the x- axis is given by: `U = 4(1 - cos 2x)`, where `x` in meters. The period of small oscillation (in sec) is
View SolutionAn object of mass `0.2 kg` executes simple harmonic oscillation along the `x - axis`with a frequency of `(25//pi) Hz`. At the position `x = 0.04`, the object has Kinetic energy of `0.5 J` and potential energy `0.4 J. The amplitude of oscillations is……m.
View SolutionThe string of a simple pendulum replaced by a uniform rod of length `L` and mass `M` while the bob has a mass `m`. It is allowed to make small oscillation. Its time period is
View Solution
A uniform semicurcular ring having mass m and radius `r` is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring is
View Solution
Two springs with negligible masses and force constants `k_1=200(N)/(m)` and `K_2=160(N)/(m)` are attached to the block of mass `m=10kg ` as shown in the fig. Initially the block is at rest, at the equilibrium position which both springs are neither stretched nor compressed. At time `t=0`, sharp impulse of `50Ns` is given to the block with a hammer along the spring.
View Solution
A thin uniform vertical rod of mass `m` and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to `k`. The mass of the spring is negligible. The frequency of small oscillation is .
View SolutionA particle executes SHM with time period 8 s. Initially, it is at its mean position. The ratio of distance travelled by it in the 1st second to that in the 2nd second is
View SolutionA particle executed S.H.M. starting from its mean position at `t=0`, If its velocity is `sqrt3bomega`, when it is at a distance b from the mean positoin, when `omega=(2pi)/(T)`, the time taken by the particle to move from b to the extreme position on the same side is
View SolutionIn a certain oscillatory system (particle is performing SHM), the amplitude of motion is 5 m and the time period is 4 s. the minimum time taken by the particle for passing betweens points, which are at distances of 4 m and 3 m from the centre and on the same side of it will approximately be
View SolutionA particle of mass `m` moving along x-axis has a potential energy `U(x)=a+bx^2` where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionThe instantaneous displacement `x` of a particle executing simple harmonic motion is given by `x=a_1sinomegat+a_2cos(omegat+(pi)/(6))`. The amplitude `A` of oscillation is given by
View SolutionA simple harmonic motion along the x-axis has the following properties: amplitude `=0.4m` the time to go from one extreme position to other is `2s` and `x=0.3m` at `t=0.5`a. the general equation of the simple harmonic motion is
View SolutionA spring balance has a scale that can read from 0 to 50 kg. The length of the scale is 20 cm. a body suspended from this balance when displaced and released oscillated harmonically with a time period of 0.6 s. The mass of the body is (take `g=10(m)/(s^2)`)
View Solution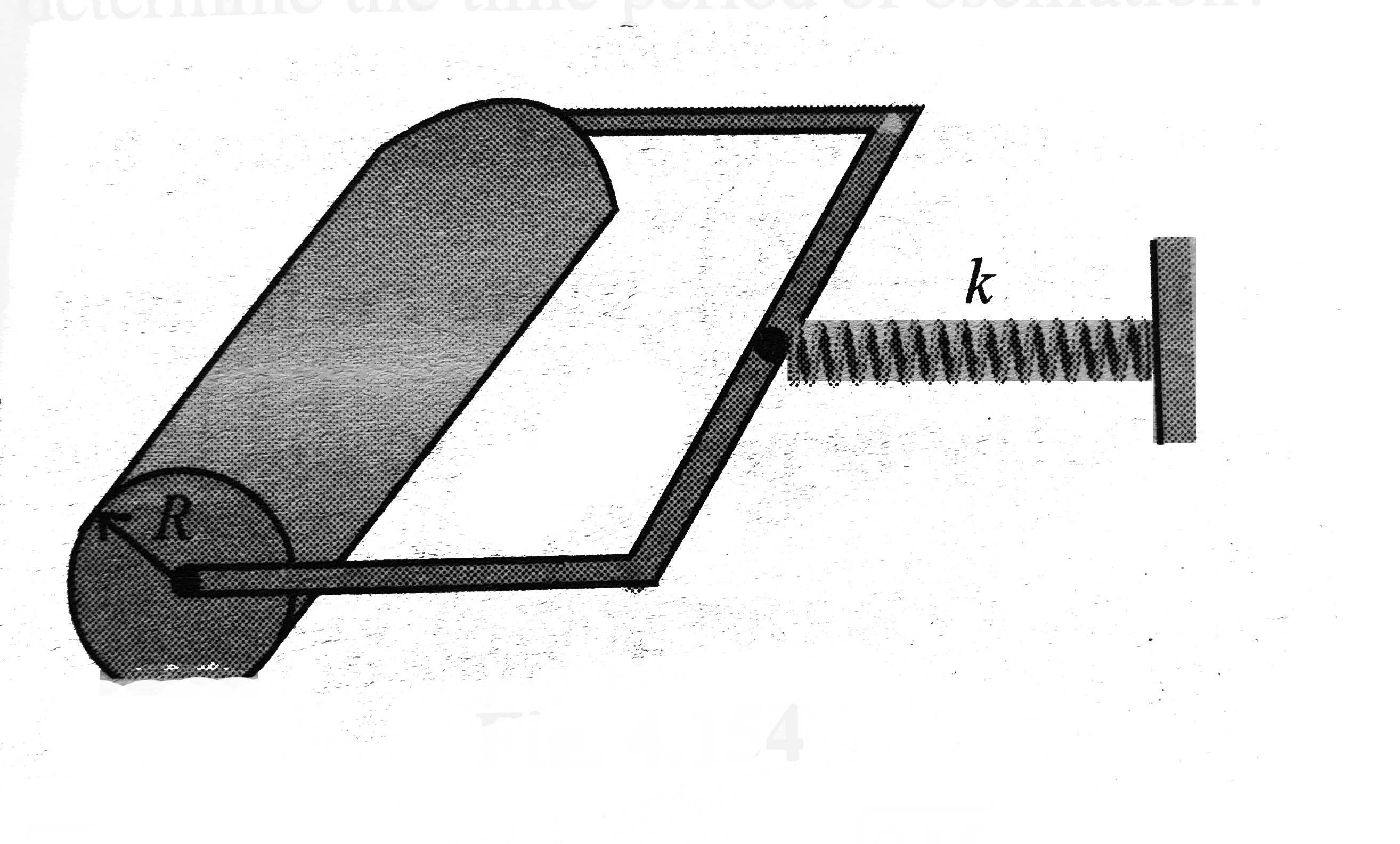
A soil cylinder of mass `M` and radius `R` is connected to a spring as shown in fig. The cylinder is placed on a rough horizontal surface. All the parts except the cylinder shown in the figure are light. If the cylinder is displaced slightly from its mean position and released, so that it performs pure rolling back and forth about its equilibrium position, determine the time period of oscillation?
View Solution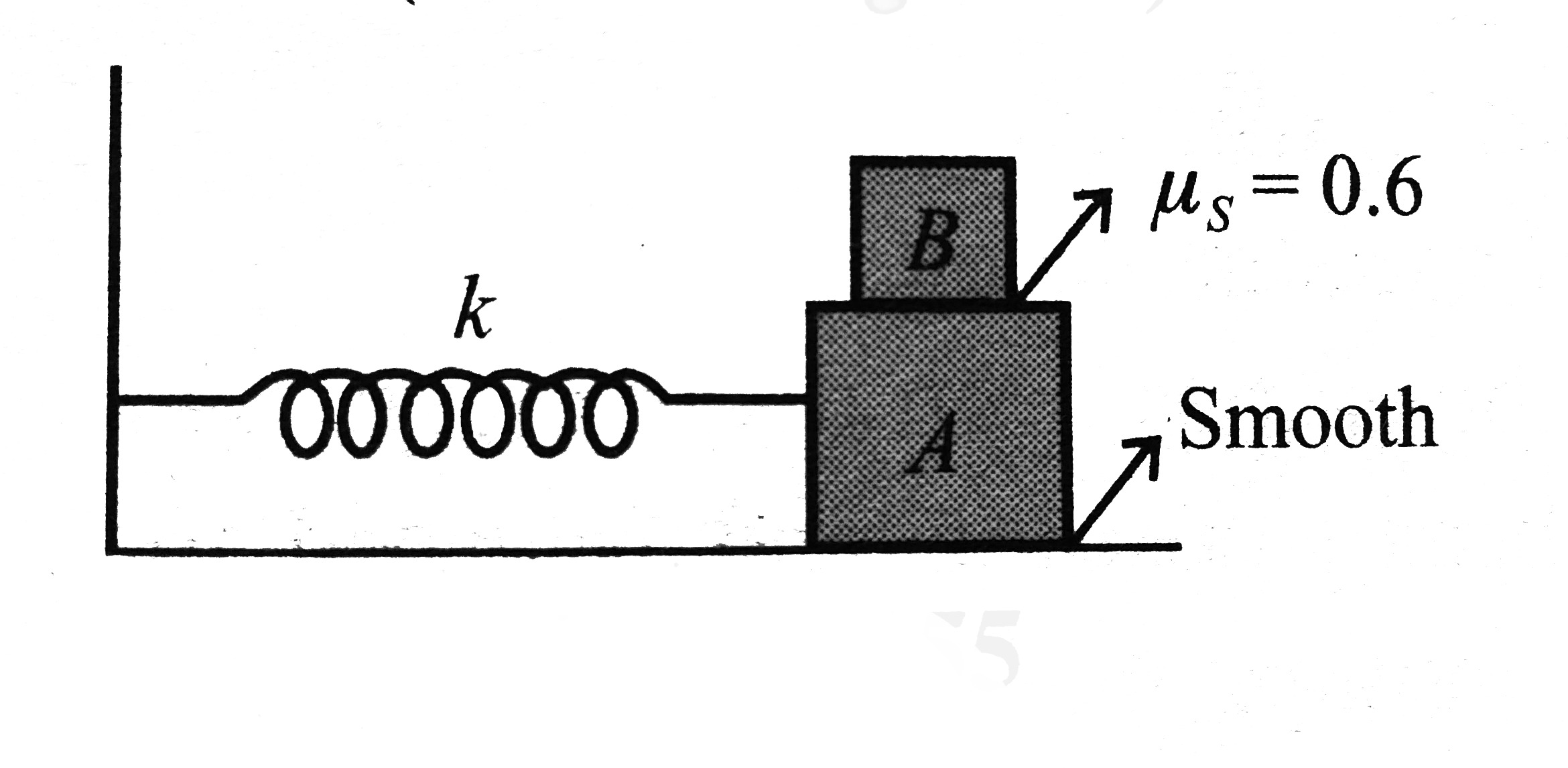
A block A is connected to spring and performs simple harmonic motion with a time period of 2 s. Another block B rests on A. The coefficient of static friction between `A` and `B` is `mu_S=0.6`. The maximum amplitude of oscillation which the system can have so that there is no relative motion between A and B is (take `pi^2=g=10`)
View SolutionA block of mass m is suspended from the ceiling of a stationary standig elevator through a spring of spring constant k. Suddenly, the cable breaks and the elevator starts falling freely. Show that the bklock now executes a simple harmonic motion of amplitude `mg/k` in the elevator
View SolutionA mass m attached to a spring of spring constant `k` is stretched a distance `x_0` from its equilibrium position and released with no initial velocity. The maximum speed attained by mass in its subsequent motion and the time at which this speed would be attained are, respectively.
View Solution
A plank of mass 12 kg is supported by two identical springs as shown is Fig. The plank always remains horizontal. When the plank is pressed down and released it performs simple harmonic motion with time period 3 s. When a block of m is attached to the plank the time priod changes to 6 s. The mass of the block is
View SolutionThe time taken by a particle performing `SHM` on a straight line to pass from point `A` to `B` where its velocities are same is `2` seconds .After another `2` seconds it return to `B` The time period of oscillation is (in seconds)
View SolutionTwo springs are made to oscillate simple harmonically due to the same mass individually. The time periods obtained are `T_1` and `T_2`. If both the springs are connected in series and hten made to oscillate by the same mass, the resulting time period will be
View Solution
A thin-walled tube of mass m and radius R has a rod of mass m and vry small cross section soldered on its inner surface. The side-view of the arrangement is as shown in the following figure. The entire arrangement is placed on a rough horizontal surface. The system is given a small angular displacement from its equilibrium position, as a result, the system performs oscillations. The time period of resulting oscillations if the tube rolls without slipping is
View SolutionA thin uniform rod of mass 1 kg and length 12 cm is suspended by a wire that passes through its centre and is perpendicular to its length.The wire is twisted and the rod is set oscillating. Time period of oscillation is found to be 3 s. When a flat triangular plate is suspended in same way through its centre of mass, the time period is found to be 6 s. The moment of inertia of the tringular plate about this axis is
View SolutionA particle performs SHM about `x=0` such that at `t=0` it is at `x=0` and moving towards positive extreme. The time taken by it to go from `x=0` to `x=(A)/(2)` is time the time taken to go from `x=(A)/(2)` to a. The most suitable option for the blank space is
View SolutionA particle performs SHM with a period `T` and amplitude a. The mean velocity of particle over the time interval during which it travels `a//2` from the extreme position is
View SolutionA particle performs simple harmonic motion about `O` with amplitude `A` and time period `T`. The magnitude of its acceleration at `t=(T)/(8)`s after the particle reaches the extreme position would be
View SolutionIn the previous question, the magnitude of velocity of particle at the mentioned instant is
View SolutionAn object of mass 4 kg is attached to a spring having spring constant `100(N)/(m)`. It performs simple harmonic motion on a smooth horizontal surface with an amplitude of 2 m. A 6 kg object is dropped vertically onto the 4 kg object when it crosses the mean position, and sticks to it. the change in amplitude of oscillation due to collision is
View SolutionA cork floating on the pond water executes a simple harmonic motion, moving up and down over a range of 4 cm. The time period of the motion is 1 s. at `t=0`, the cork is at its lowest position of oscillation, the position and velocity of the cork at `t=10.5s`, would be
View SolutionA spring is placed in vertical position by suspending it from a hook at its top. A similar hook on the bottom of the spring is at 11 cm above a table top. A mass of 75 g and of negligible size is then suspended from the bottom hook, which is measured to be 4.5 cm above the table top. The mass is then pulled down a distance of 4 cm and released. Find the approximate. Position of the bottom hook after 5 s? Take `g=10(m)/(s^2)` and hook's mass to be negligible.
View SolutionA particle is performing `SHM` according to the equation `x=(3cm)sin((2pi)/(18)+(pi)/(6))`, where t is in seconds. The distance travelled by the particle in 39 s is
View Solution
Two springs, each of unstretched length 20 cm but having different spring constant `k_1=1000(N)/(m)` and `k_2=3000(N)/(m)` are attached to two opposite faces of a small block of mass `m=100g` kept on a smooth horizontal surface as shown in fig. The outer ends of the two springs are now attached to two pins `P_1` and `P_2` whose locations are shown in the figure. as a result of this, the block acquires a new equilibrium position. The block has been displaced by small amount from its equilibrium position and released to perform simple harmonic motion: then
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression `U=(a)/(x^2)-(b)/(x)`, where a and b are positive constant. The particle will perform.
View SolutionA particle performing simple harmonic motion having time period 3 s is in phase with another particle which also undergoes simple harmonic motion at `t=0`. The time period of second particle is T (less that 3s). If they are again in the same phase for the third time after 45 s, then the value of T will be
View SolutionA particle performs `SHM` on x- axis with amplitude `A ` and time period period `T` .The time taken by the particle to travel a distance `A//5` string from rest is
View Solution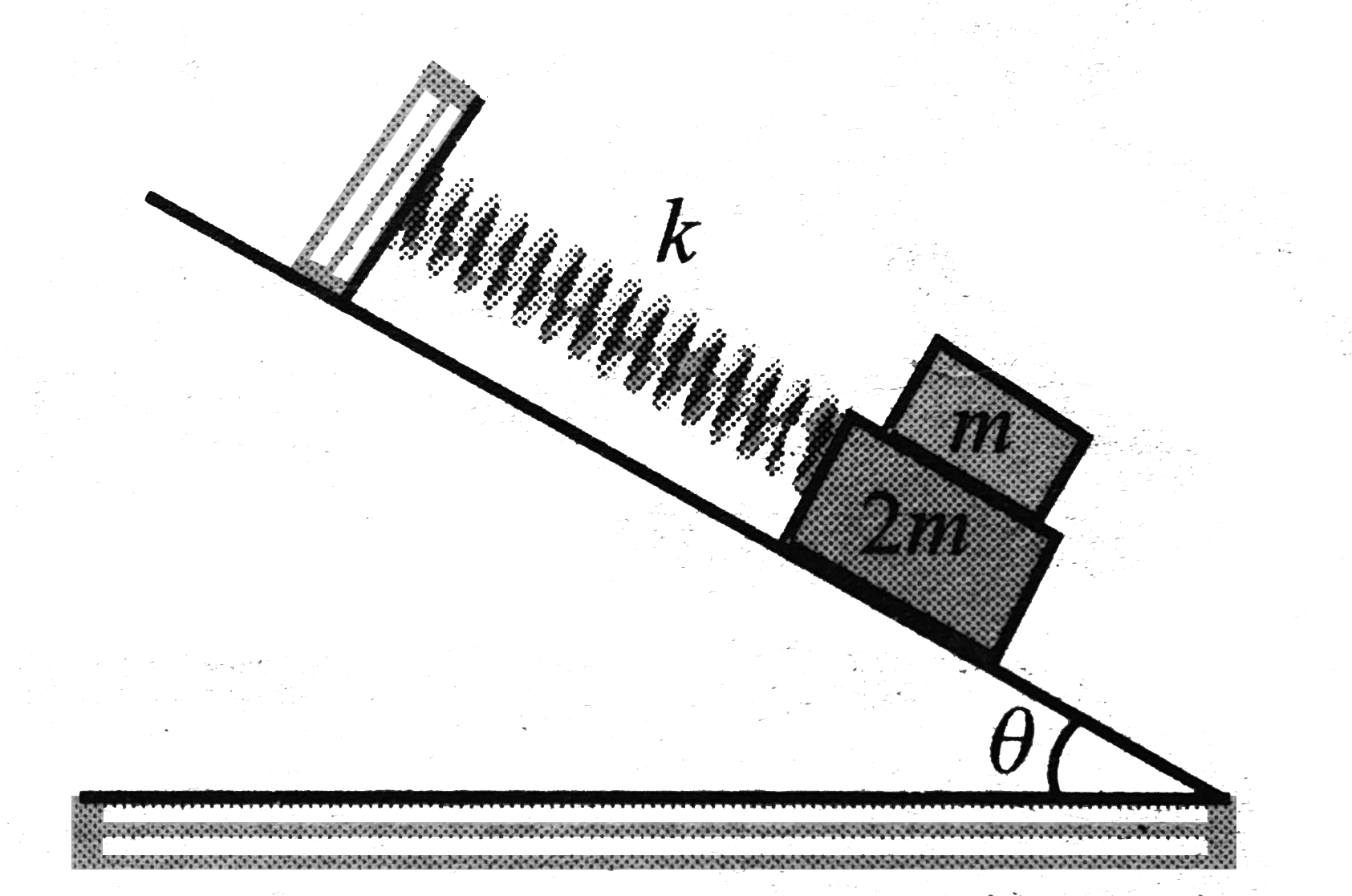
The coefficient of friction between block of mass m and `2m` is `mu=2tantheta`. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View Solution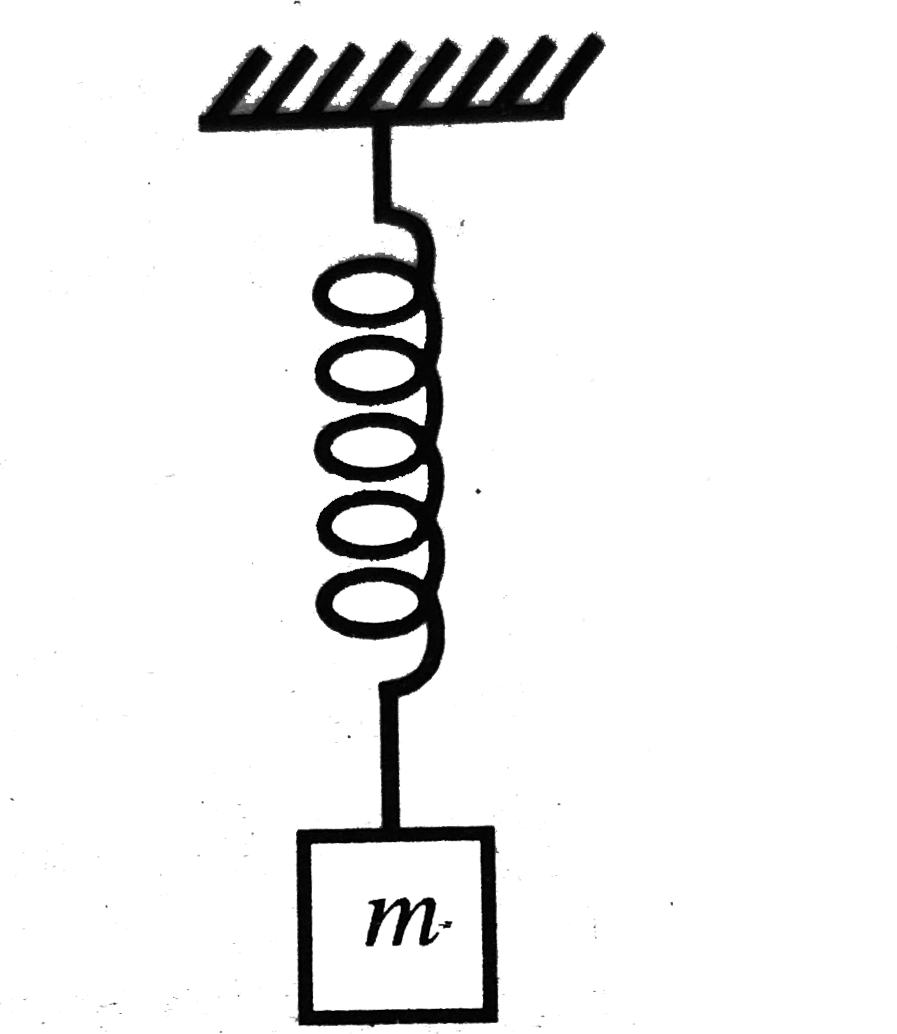
A block of mass `m` is suspended from a spring and executes vertical SHM of time period T as shown in Fig. The amplitude of the SHM is A and spring is never in compressed state during the oscillation. The magnitude of minimum force exerted by spring on the block is
View SolutionA particle performs `SHM` of amplitude `A` along a straight line .When it is at a distance of `sqrt(3)/(2)`A from mean position its kinetic energy gets increased by an amount of `(1)/(2) m omega^(2)A^(2)` due to an impulsive force. Then its new amplitude becomes
View SolutionA horizontal spring -block system of mass `2kg` executes `S.H.M` when the block is passing through its equilibrium position an object of mass `1kg` is put on it the two move together The new amplitude of vibration is `(A` being its initial amplitude)
View Solution
A metre stick swinging in vertical plane about a fixed horizontal axis passing through its one end undergoes small oscillation of frequency `f_0`. If the bottom half of the stick were but off, then its new frequency of small oscillation woul become.
View SolutionA physical pendulum is positioned so that its centre of gravity is above the suspension point. When the pendulum is realsed it passes the point of stable equilibrium with an angular velocity `omega`. The period of small oscollations of the pendulum is
View SolutionA particle executing harmonic motion is having velocities `v_1` and `v_2` at distances is `x_1` and `x_2` from the equilibrium position. The amplitude of the motion is
View Solution
A wire is bent an an angle `theta`. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View Solution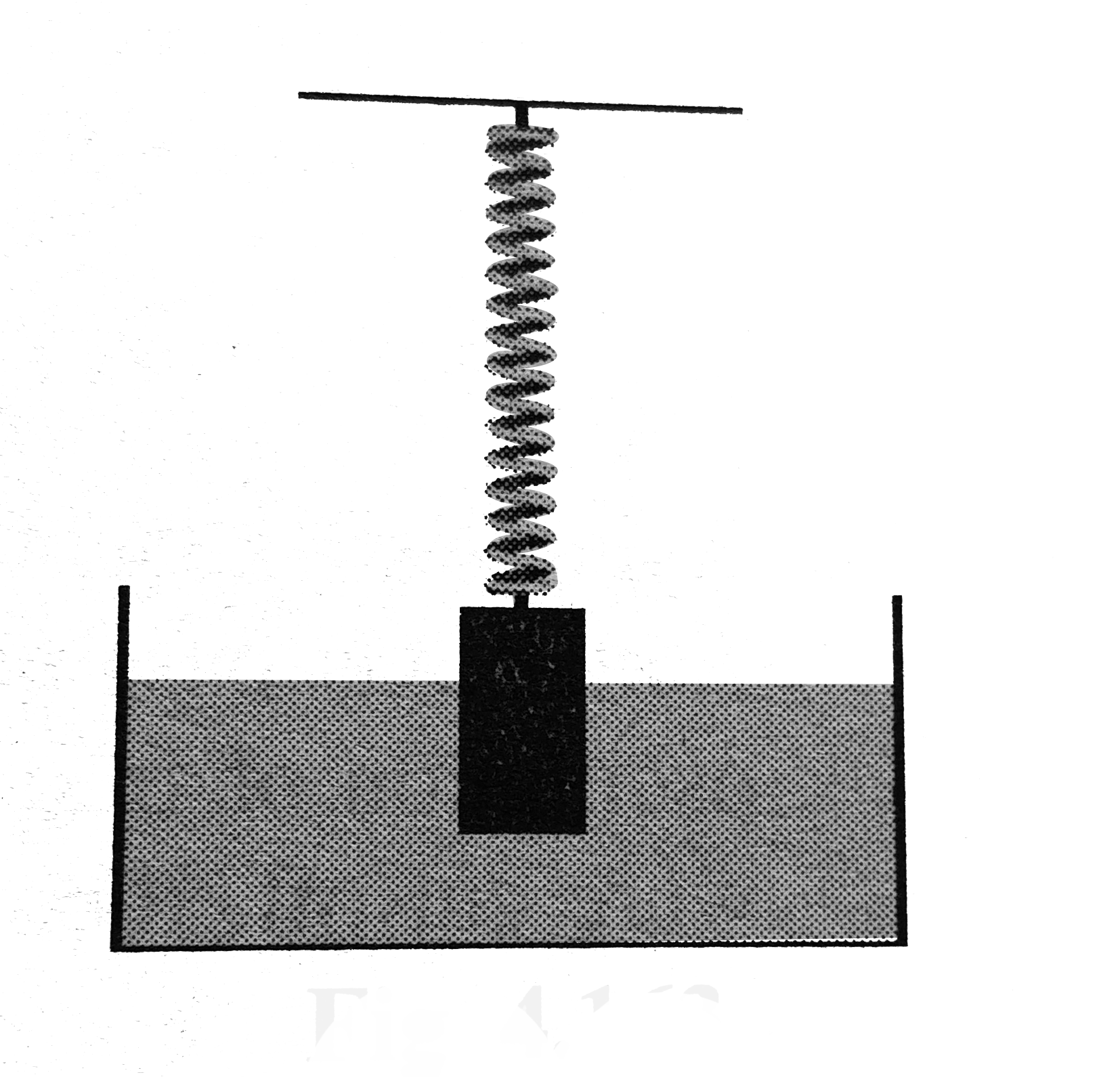
A solid right circular cylinder of weight 10 kg and cross sectional area `100cm^2` is suspended by a spring, where `k=1(kg)/(cm)`, and hangs partially submerged in water of density `1000(kg)/(m^3)` as shown in Fig. What is its perod when it makes simple harmonic vertical oscillations? (Take `g=10(m)/(s^2)`)
View Solution
A block `A` of mass m is placed on a smooth horizontal platform P and between two elastic massless springs `S_1` and `S_2` fixed horizontally to two fixed vertical walls. The elastic constants of the two springs are equal to k and the equilibrium distance between the two springs both in relaxed states is d. The block is given a velocity `v_0` initially towards one of the springs and it then oscillated between the springs. The time period `T` of oscillations and the minimum separation `d_m` of the spring will be
View SolutionA certain simple harmonic vibrator of mass 0.1 kg has a total energy of 10 J. Its displacement from the mean position is 1 cm when it has equal kinetic and potential energies. The amplitude A and frequency n of vibration of the vibrator are
View SolutionA simple pendulum of length `l` and mass `m` is suspended in a car that is moving with constant speed `v` around a circle of radius `r`. Find the period of oscillation and equilibrium position of the pendulum.
View Solution
One end of a spring of force constant K is fixed to a vertical wall and the other to a body of mass m resting on a smooth horizontal surface. There is another wall at a distance `x_0` from the body. The spring is then compressed by `3x_0` and released. The time taken to strike the wall from the instant of release is (given `sin^-1((1)/(3))=((pi)/(9))`)
View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.

View SolutionA uniform stick of mass `M` and length `L` is pivoted its come its ends are attached to two spring each of the constant `K`. In the position shown in figure the same through a small length when spring is display through a small angle of and released. The stick :
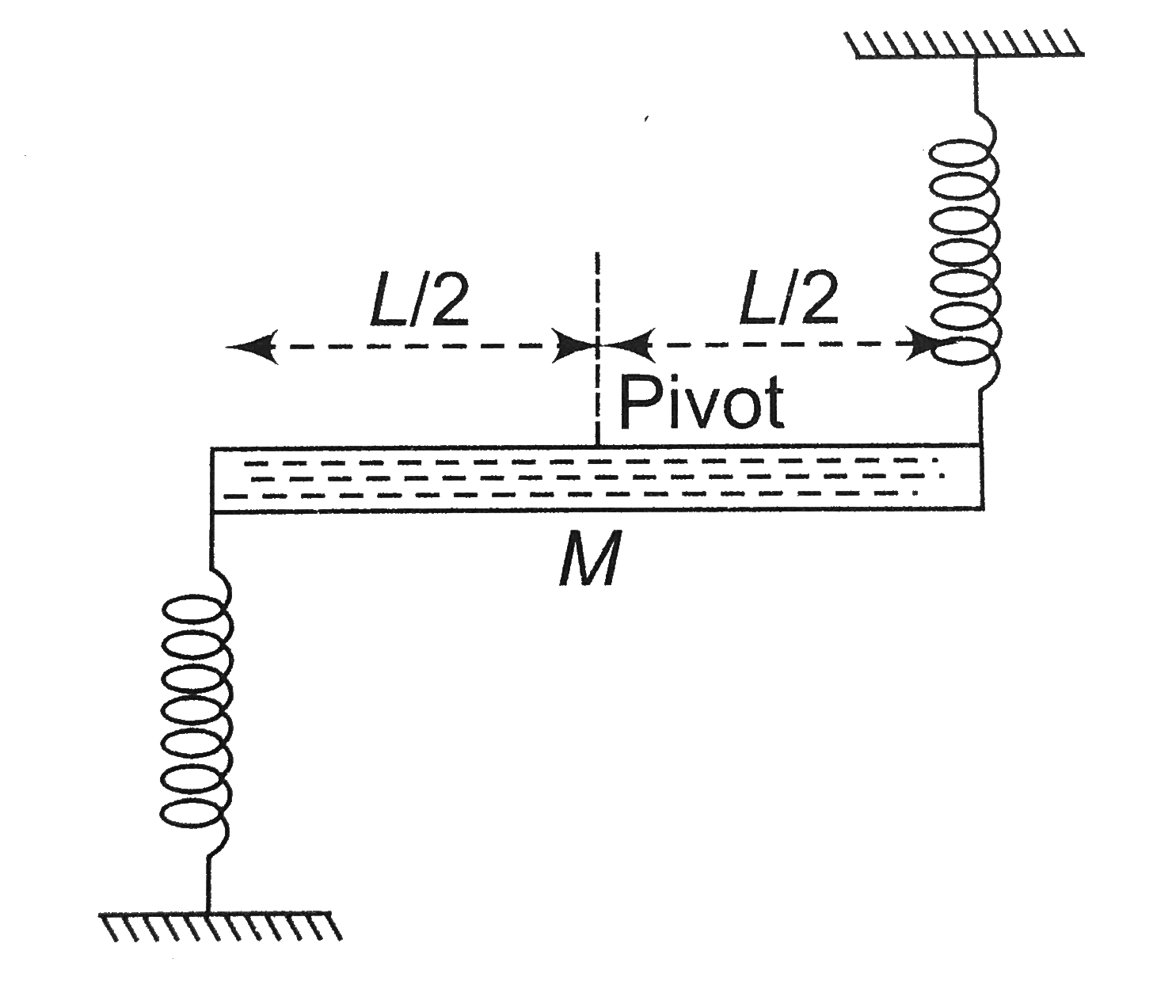
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA street car moves rectilinearly from station A to the next station B (from rest to rest) with an acceleration varying according to the law `f = a-bx,` where a and b are constants and x is the distance from station A. The distance between the two stations and the maximum velocity are
View SolutionTwo particle `P` and `Q` describe `S.H.M.` of same amplitude a same frequency `f` along the same straight line .The maximum distance between the two particles is `asqrt(2)` The phase difference between the two particle is
View SolutionThe velocity `v` of a particle of mass is moving along a straight line change with time `t` as `(d^(2)v)/(dt^(2)) = - Kv` where `K` is a particle constant which of the following statement is correct?
View Solution
The oscillations represented by curve 1 in the graph are expressed by equation`x=Asinomegat.` The equation for the oscillation represented by curve `2` is expressed as
View Solution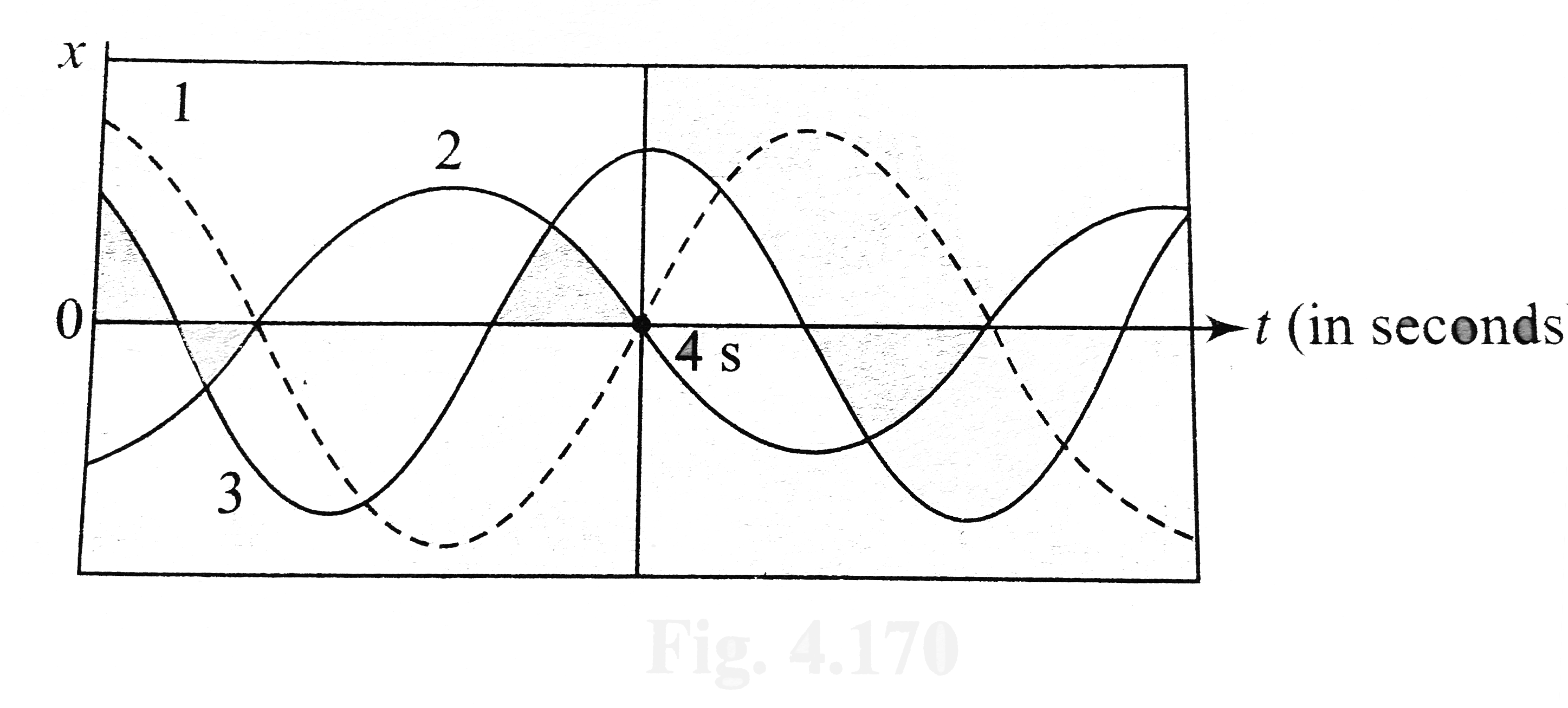
Graph shows the `x(t)` curves for the three experiments involving a particular spring block system oscillating in SHM. The kinetic energy of the system is maximum at `t=4` s. For the situation.
View SolutionThe acceleration of a particle moving along x-axis is `a=-100x+50`. It is released from `x=2`. Here `a` and `x` are in S.I units. The motion of particle will be:
View SolutionIn the above question, the speed of the particle at origin will be:
View SolutionA particle performs `SHM` of amplitude `A` along a straight line .When it is at a distance of `sqrt(3)/(2)`A from mean position its kinetic energy gets increased by an amount of `(1)/(2) m omega^(2)A^(2)` due to an impulsive force. Then its new amplitude becomes
View Solution
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle `theta` from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View SolutionA small mass executes linear `SHM` about `O` with amplitude a and period `T`. Its displacement from `O` at time `T//8` after passing through `O` is:
View SolutionTime period of a particle executing `SHM` is `8` sec. At `t=0` it is at the mean position. The ratio of the distance covered by the particle in the `1st` second to the `2nd` second is:
View SolutionA particle performs SHM with a period `T` and amplitude a. The mean velocity of particle over the time interval during which it travels `a//2` from the extreme position is
View SolutionA graph of the square of the velocity against the square of the acceleration of a given simple harmonic motion is
View SolutionA plank with a small block on top of it is under going vertical `SHM`. Its period is `2 sec`. The minimum amplitude at which the block will separate from plank is :
View SolutionThe potential energy of a simple harmonic oscillator of mass 2 kg in its mean position is 5 J. If its total energy is 9 J and its amplitude is 0.01 m, its time period would be
View SolutionA spring mass system preforms `S.H.M` if the mass is doubled keeping amplitude same, then the total energy of `S.H.M` will become :
View Solution
Single Correct questions and complete solutions for chapter LINEAR AND ANGULAR SIMPLE HARMONIC MOTION of CENGAGE PHYSICS (HINGLISH) of Class 11