Complete Solutions to Exercise 4.1 of chapter LINEAR AND ANGULAR SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LINEAR AND ANGULAR SIMPLE HARMONIC MOTION |
| CENGAGE PHYSICS | Exercise 4.1 |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
i.The acceleration versus time graph of a partical SHM is shown in the figure . Plot the displacement versus time graph
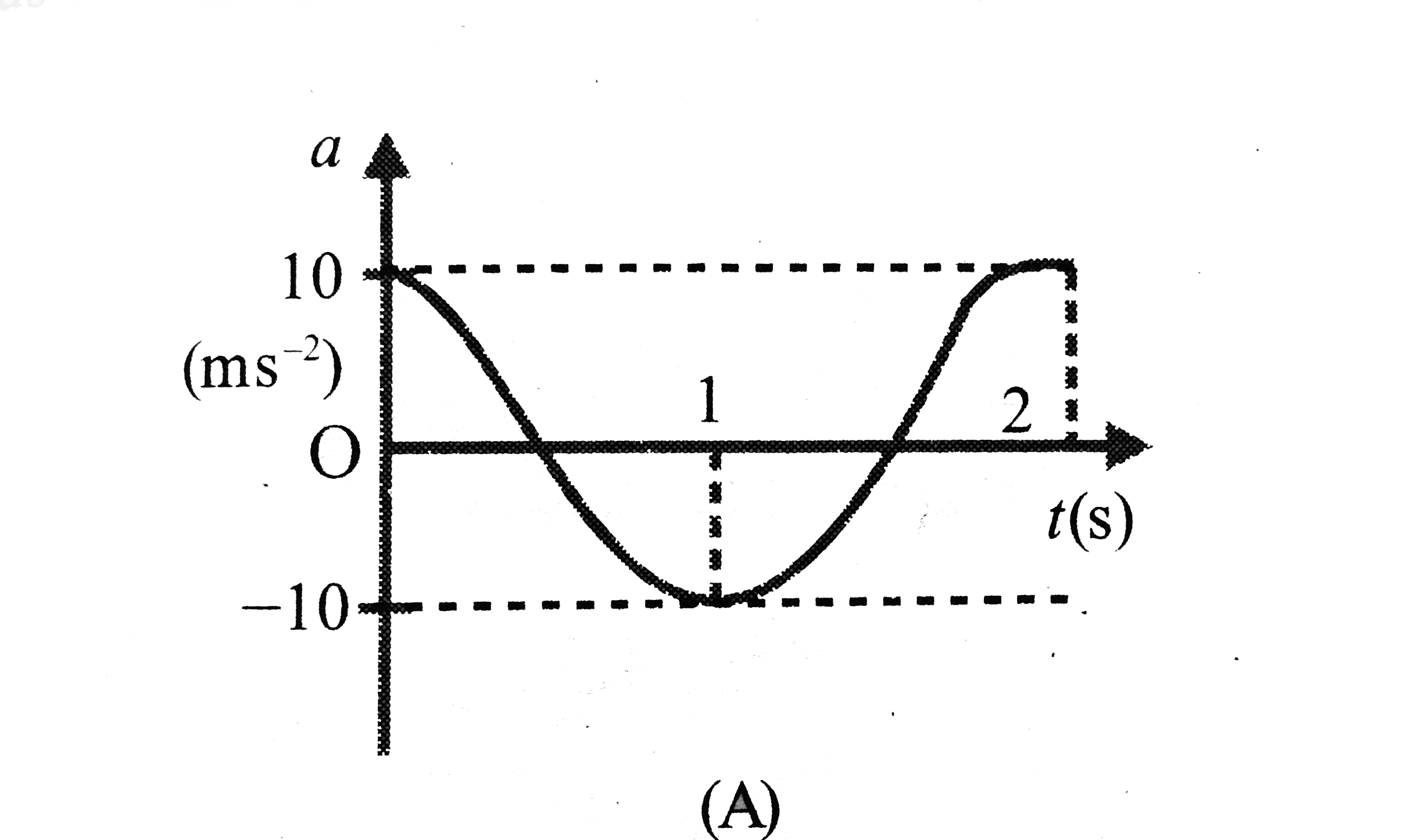
ii. The frection of oscillation is……..
iii. The displacement amplitude is ………
iv. At `t = 0`, the velocity of the partical is ......
v. The kinetic energy of the partical is maximum at `t = `....... and t = ......
vi. The potential energy is maximum at t = ....... : t = ..... ans t = .........05:44View SolutionA partical slides back and forth between two inclined friction lessplanes.

a. If h is the initial height of the partical, the period of oscillation……
b. Is the motion oscillatory? Is it SHM?02:26View SolutionThe equation of displacement of two waves are given as
` y_(1) = 10 sin( 3 pi t + (pi)/(3)) , y_(2) = 5 [ sin 3 pi t + sqrt(3) cos 3 pi t]`
Then what is the ratio of their amplitudes01:59View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
04:57View SolutionThe equation of motion of a particle started at `t=0` is given by `x=5sin(20t+pi//3)` where x is in centimeter and t in second. When does particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?03:21View SolutionA partical starts SHM frommean position O executing SHM A and B are the two point at which its velocity is zero . It passes through a cartain point O at time `t_(1) = 0.5 and t_(2) = 1.5 s` with a speed of `3 m//s`.

i. The maximum speed .......
ii. ratio `AP//PB` .....07:26View SolutionIf the maximum speed and acceleration of a partical executing SHM is `20 cm//s and 100 cm//s`, find the time period od oscillation.
01:17View SolutionA partical is performing SHM of amplitude 'A' and time period 't'. Find the time taken by the partical to go from `0 to A//2`.
01:15View SolutionA particle of mass `2 kg` is moving of a straight line under the actin force `F = (8 - 2x)N`. It is released at rest from `x = 6m`.
a. Is the particle moving simple hormonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.04:23View SolutionA partical executing simple harmonic motion has amplitude of `1 m` and time period `2 s At t = 0`, net force on the partical is zero. Find the equation of displacement of the partical.
01:12View SolutionIn the previous question, find maximum velocity and maximum acceleration.
01:21View SolutionA partical in SHM ha a period of 4s .It takes time `t_(1)` to start from mean position and reach half the amplitude. In another case it taken a time `t_(2)` to start from mean position and reach half the amplitude. Find the ratio `t_(1)//t_(2)`
02:08View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
01:57View SolutionA particle executes SHM of period `1.2 s` and amplitude `8cm`. Find the time it takes to travel `3cm` from the positive extremity of its oscillation. `[cos^(-1)(5//8) = 0.9rad]`
02:40View SolutionA cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by `x =A cos (omega t).` There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................
08:14View SolutionThe figure shows the displacement-time graph of a particle executing `SHM`. If the time period of oscillation is `2s`, then the equation of motion is given by
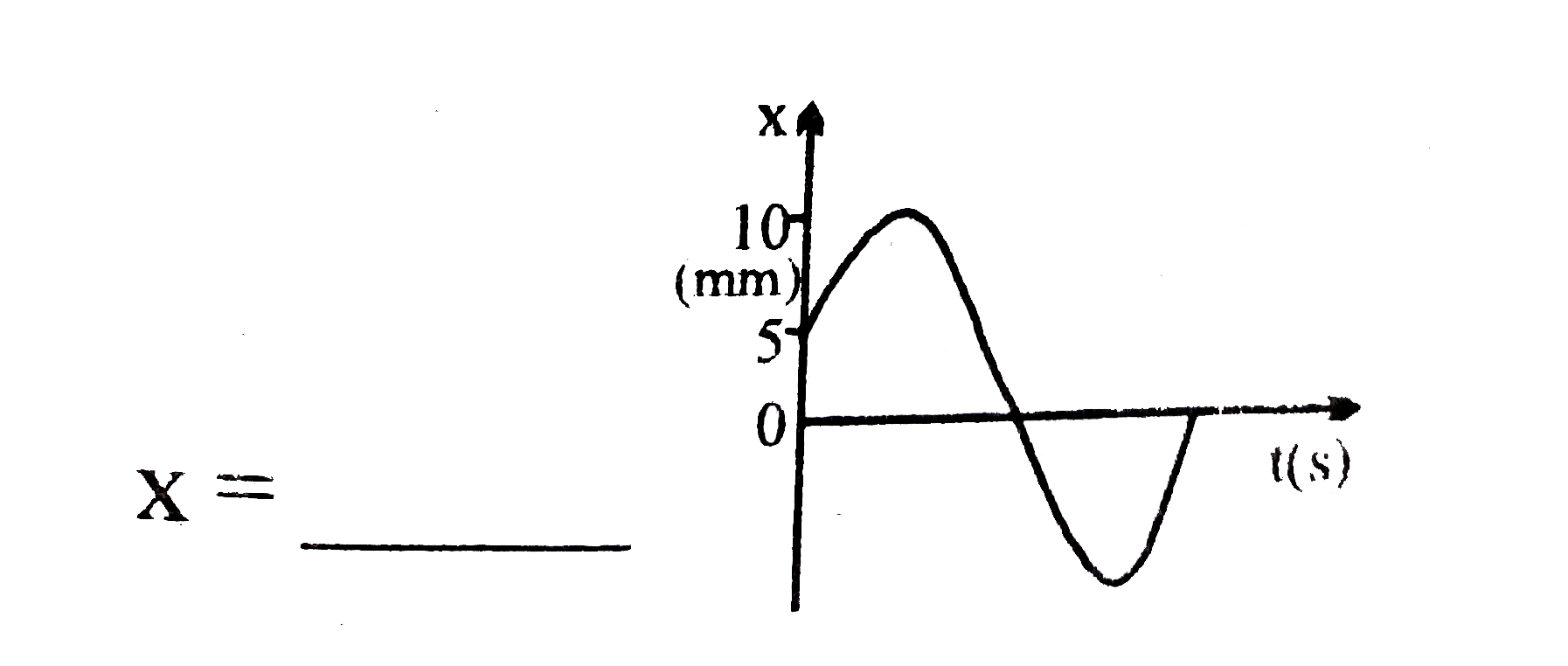 01:48View Solution
01:48View SolutionA boby excuting SHM has its velocity its `10 cm//see and7 cm//see` when its displacement from themean positionare `3 cm` and `4 cm` , respectively. Calculate the length of the path.
02:53View SolutionA body undergoing `SHM` about the origin has its equation is given by `X=0.2 cos 5pit`. Find its average speed from `t=0 to t=0.7 sec`.
05:59View SolutionThe acceleration-displacement `(a-X)` graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.
 02:01View Solution
02:01View SolutionA block is kept on a horizontal table. The stable is undergoing simple harmonic motion of frequency `3Hz` in a horizontal plane. The coefficient of static friciton between block and the table surface is `0.72.` find the maximum amplitude of the table at which the block does not slip on the surface.
04:07View SolutionA linear harmonic oscillator has a total mechanical energy of `200 J`. Potential energy of it at mean position is `50J`. Find
(i) the maximum kinetic energy,
(ii)the minimum potential energy,
(iii) the potential energy at extreme positions.04:21View SolutionThe potential energy of a particle oscillating along x-axis is given as
`U=20+(x-2)^(2)`
Here, `U` is in joules and `x` in meters. Total mechanical energy of the particle is `36J`.
(a) State whether the motion of the particle is simple harmonic or not.
(b) Find the mean position.
(c) Find the maximum kinetic energy of the particle.03:36View Solution`x_(1) = 3 sin omega t`
` x_(2) = 5 sin (omega t + 53^(@))`
`x_(3) = - 10 cos omega t`
Find amplitude of resultant SHM.04:38View Solution
Exercise 4.1 questions and complete solutions for chapter LINEAR AND ANGULAR SIMPLE HARMONIC MOTION of CENGAGE PHYSICS (HINGLISH) of Class 11
