Complete Solutions to Single Correct of chapter RIGID BODY DYNAMICS 1 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 1 |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 97 |
| Academic Year | 2023-24 |
Two rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
01:31View SolutionThe moment of inertia of a solid sphere about an axis passing through the centre radius is `1/2MR^(2)` , then its radius of gyration about a parallel axis t a distance `2R` from first axis is
01:31View SolutionFrom a given sample of uniform wire, two circular loops `P` and `Q` are made, `P` of radius `r` and `Q` of radius `nr`. If the M.I. of `Q` about its axis is four times that of `P` about its axis (assuming the wire to be of diameter much smaller than either radius), the value of n is
02:45View SolutionTwo circular discs `A` and `B` of equal masses and thicknesses. But are made of metals with densities `d_A and d_B (d_A gt d_B)`. If their moments of inertia about an axis passing through the centre and normal to the circular faces be `I_A and I_B`, then.
02:09View SolutionFour identical rods are joined end to end to form a square. The mass of each rod is `M`. The moment of inertia of the square about the median line is
02:10View SolutionTwo circular iron discs are of the same thickness. The diameter of A is twice of B . The moment of inertia of A as compared to that of B is
03:18View SolutionTwo thin discs each of mass `M` and radius `r` are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc `B` and passing through its centre is :
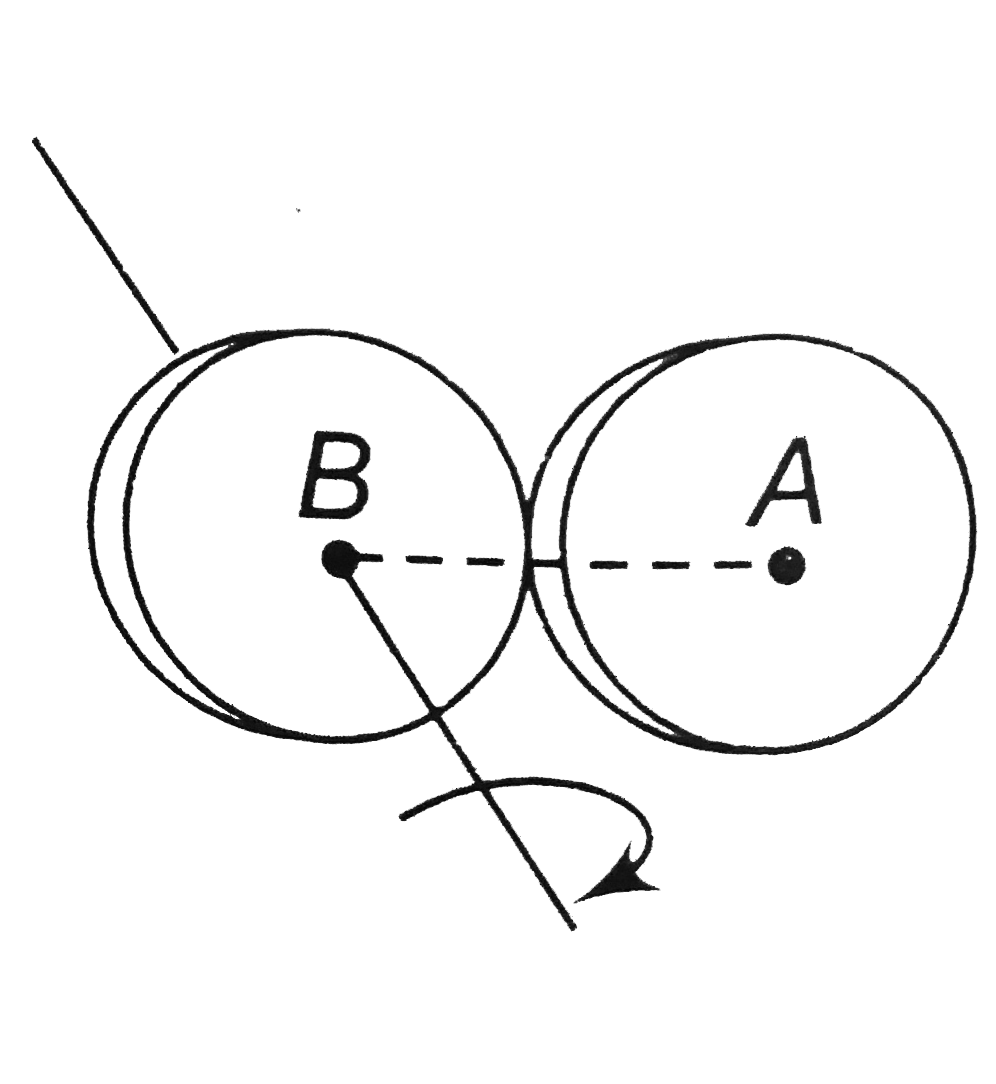 .02:56View Solution
.02:56View SolutionAn isosceles triangular piece is cut a square plate of side `l`. The piece is one-fourth of the square and mass of the remaining plate is `M`. The moment of inertia of the plate about an axis passing through `O` and perpendicular to its plane is
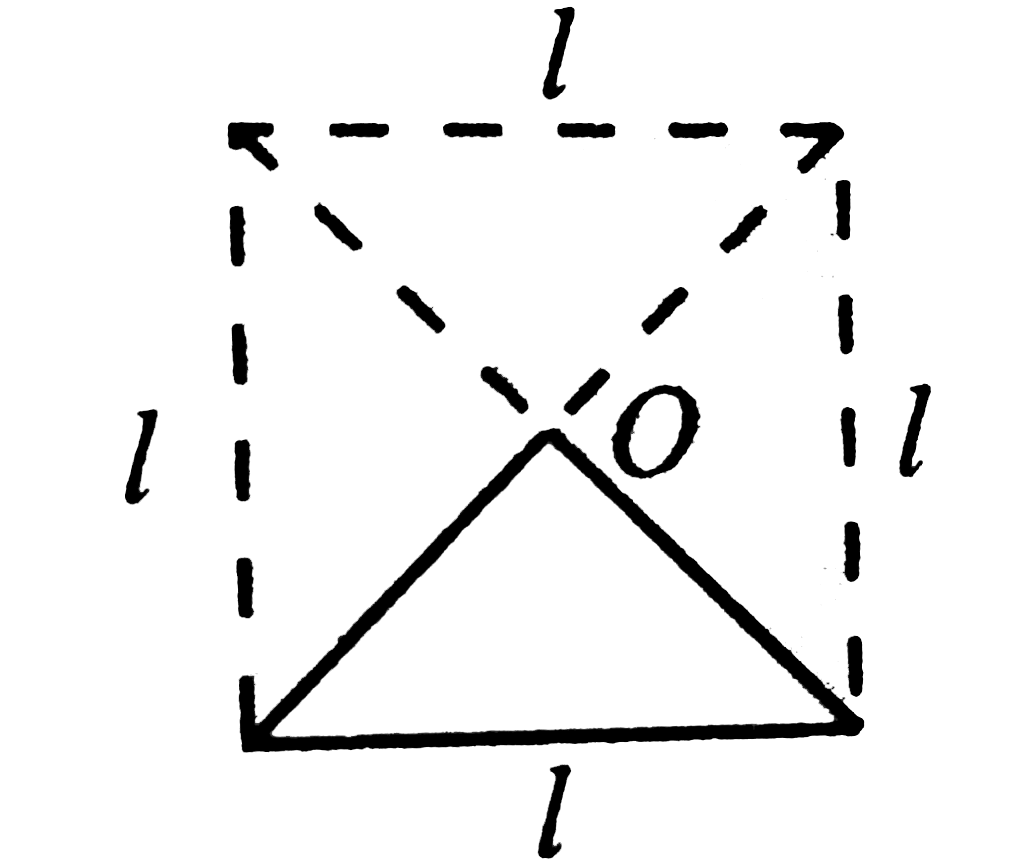 03:21View Solution
03:21View SolutionThree rings, each of mass `m` and radius `r`, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
 02:49View Solution
02:49View SolutionThree identical rods, each of mass `m` and length `l`, form an equaliteral triangle. Moment of inertia about one of the sides is
 04:50View Solution
04:50View SolutionAbout which axis moment of inertia in the given triangular lamina is maximum?
 08:16View Solution
08:16View Solution
A square is made by joining four rods each of mass `M` and length `L`. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner is06:32View SolutionFigure shows a uniform solid block of mass `M` and edge lengths `a, b` and `c`. Its `M.I`. about an axis through one edge and perpendicular (as shown) to the large face of the block is
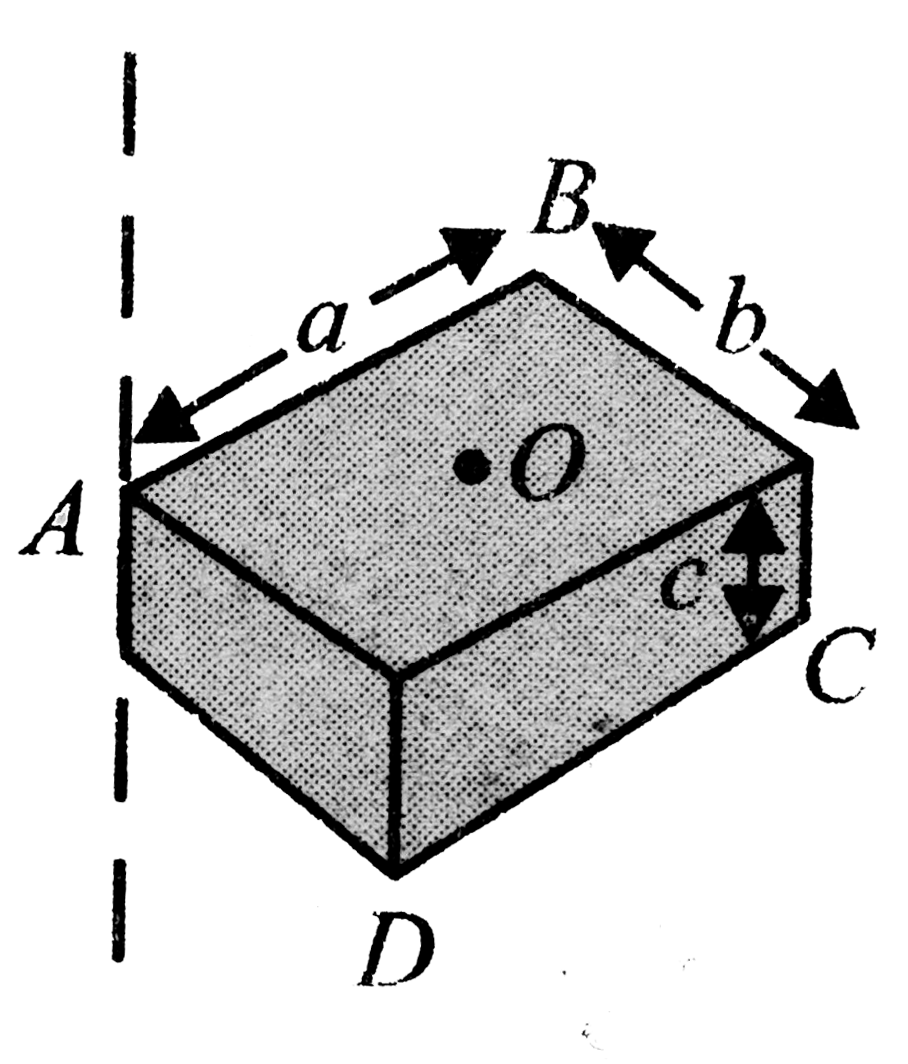 03:40View Solution
03:40View SolutionIn a rectangle `ABCD, AB = 21` and `BC = 1`. Axes `xx` and `yy` pass through centre of the rectangle. The moment of inertia is least about :
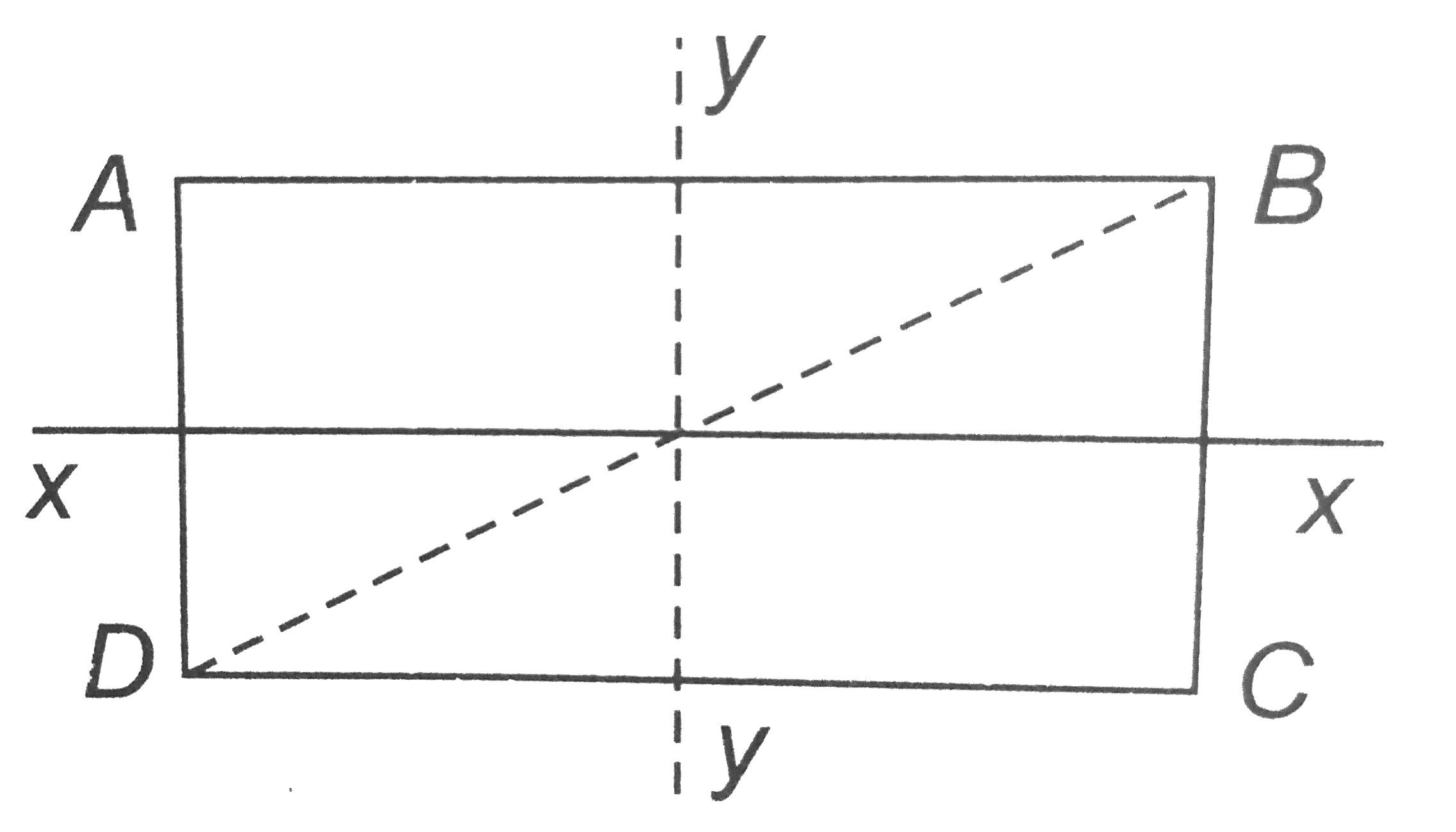 .03:36View Solution
.03:36View SolutionFigure shows a thin metallic triangular sheet `ABC`. The mass of the sheet is `M`. The moment of inertia of the sheet about side `AC` is :
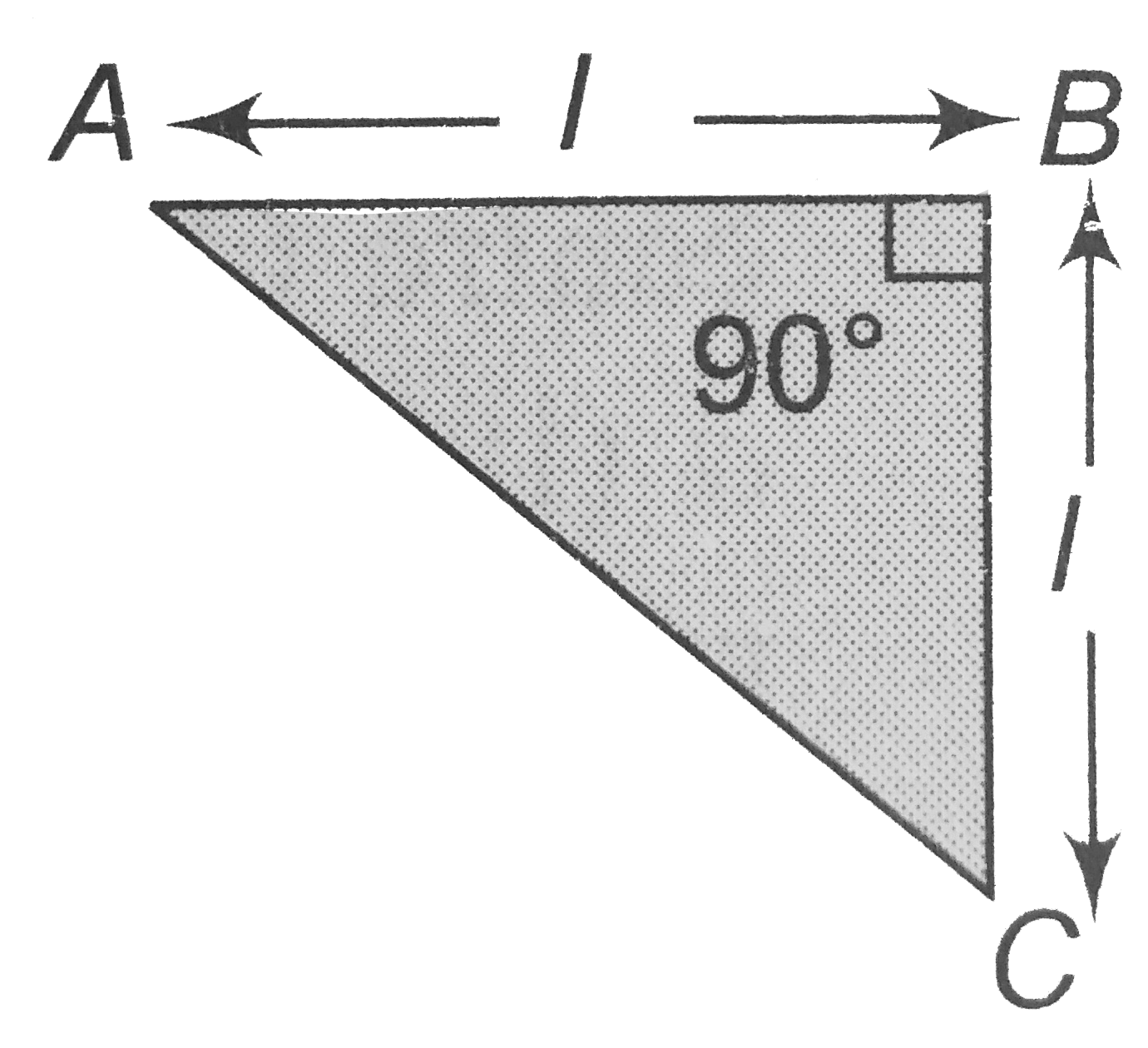 .02:45View Solution
.02:45View SolutionThe moment of inertia of a door of mass `m`, length `2 l` and width `l` about its longer side is.
01:25View SolutionA disc of radius `R` rolls without slipping at speed `v` along positive `x`-axis. Velocity of point `P` at the instant shown in Fig. is
 02:18View Solution
02:18View SolutionA disc of radius `R` rolls on a horizontal ground with linear acceleration `a` and angular acceleration `alpha` as shown in Fig. The magnitude of acceleration of point `P` as shown in the figure at an instant when its linear velocity is `v` and angular velocity is `omega` will be a
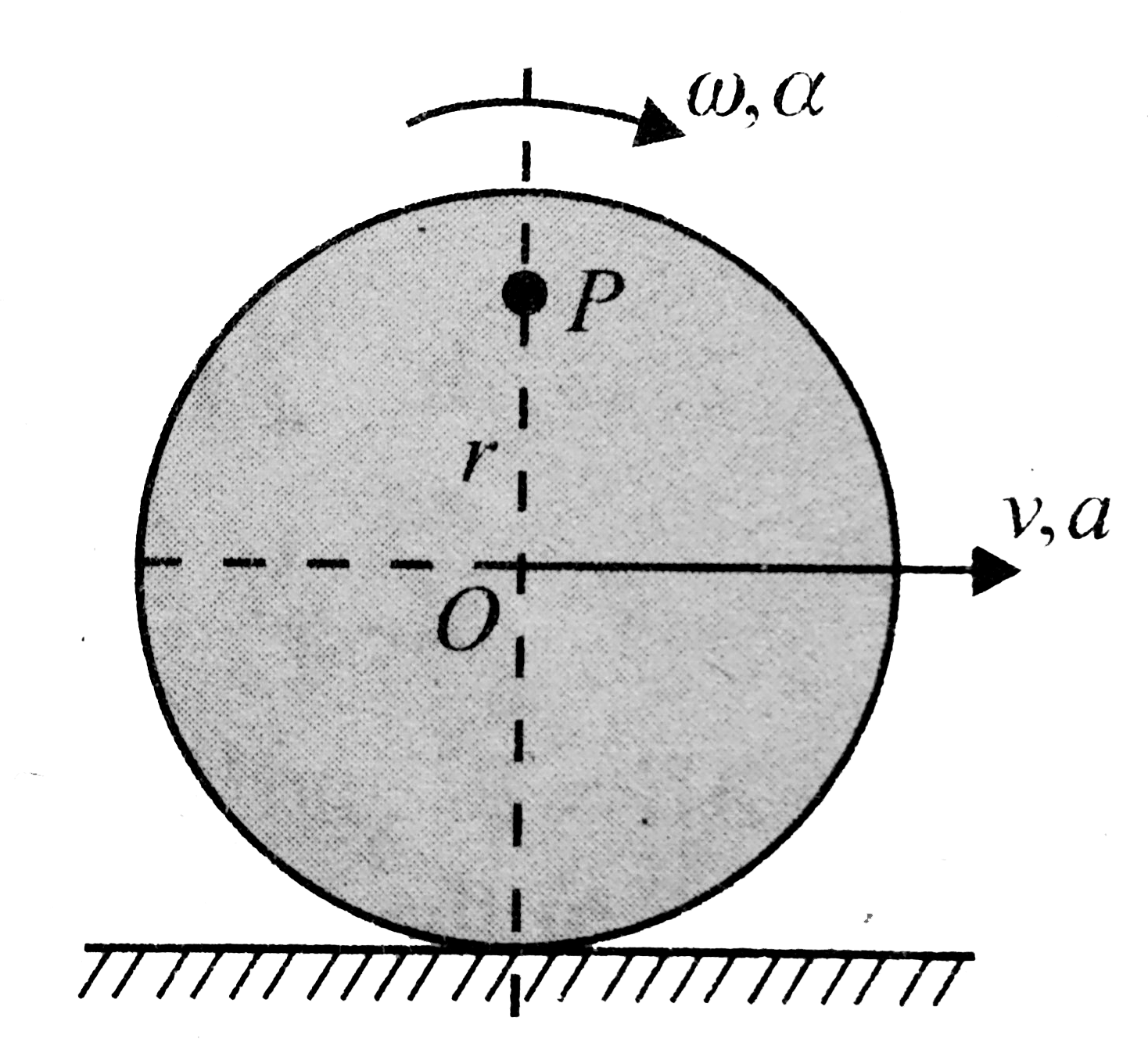 02:46View Solution
02:46View SolutionA uniform disc of mass `M` and radius `R` is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull `T` is exerted on the cord. The angular acceleration of the disc is
01:43View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
01:31View SolutionThe moment of inertia of a solid sphere about an axis passing through the centre radius is `1/2MR^(2)` , then its radius of gyration about a parallel axis at a distance `2R` from first axis is
01:31View SolutionA triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to the plane of the paper and
(i) passing through `A`,
(ii) passing through `B`, by the application of some force `F` at `C` (mid - point AB) as shown in the figure. In which case angular acceleration is more ?
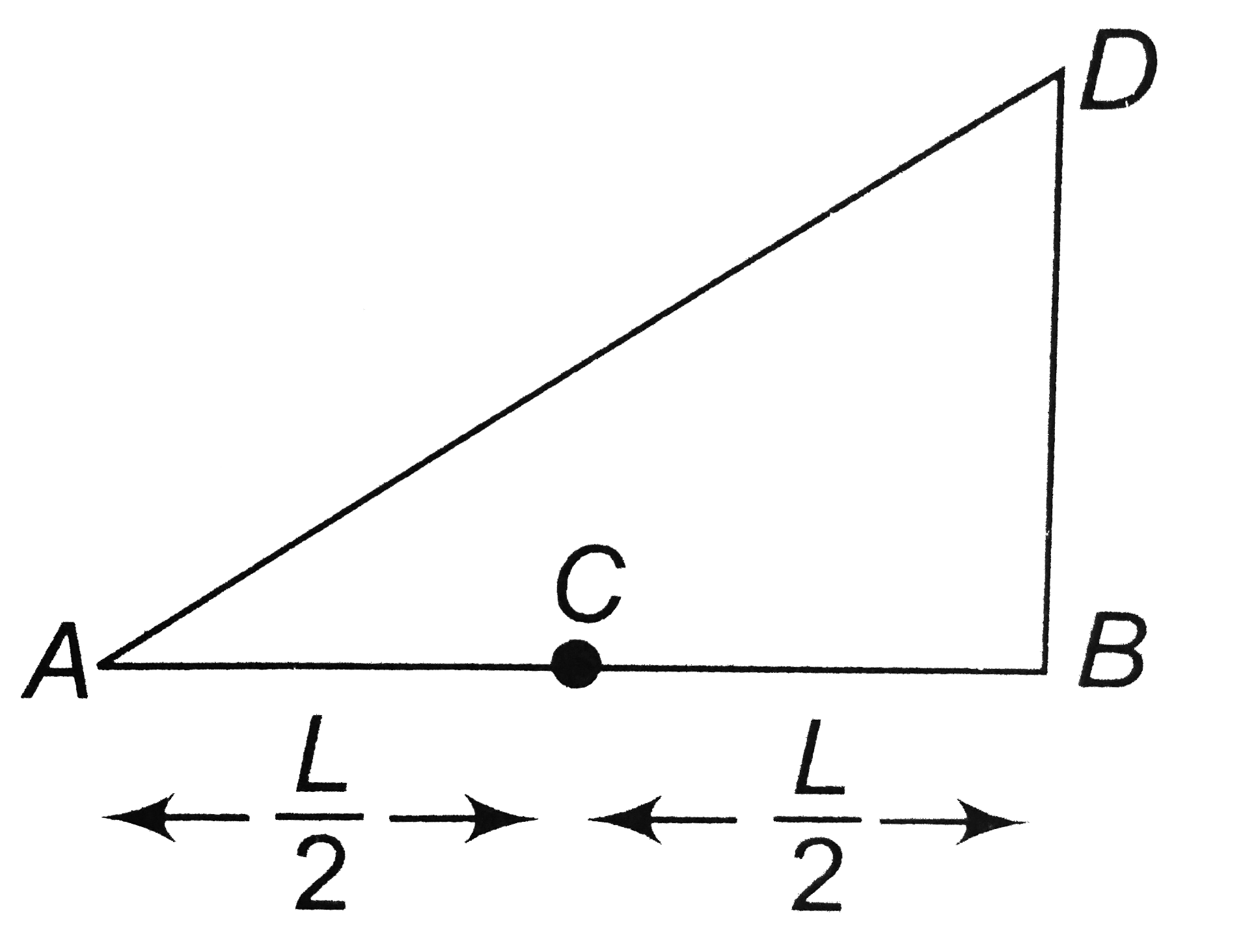 .01:43View Solution
.01:43View SolutionA uniform rod of length `L` and mass `M` is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at an angle `theta` with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?03:15View SolutionIn Fig, the bar is uniform and weighing `500 N`. How large must `W` be if `T_(1)` and `T_(2)` are to be equal?
 03:51View Solution
03:51View SolutionIn an experiment with a beam balance, an unknown mass `m` is balanced by two known masses of `16 kg` and `4 kg` shown in Fig. The value of the unknown mass `m` is
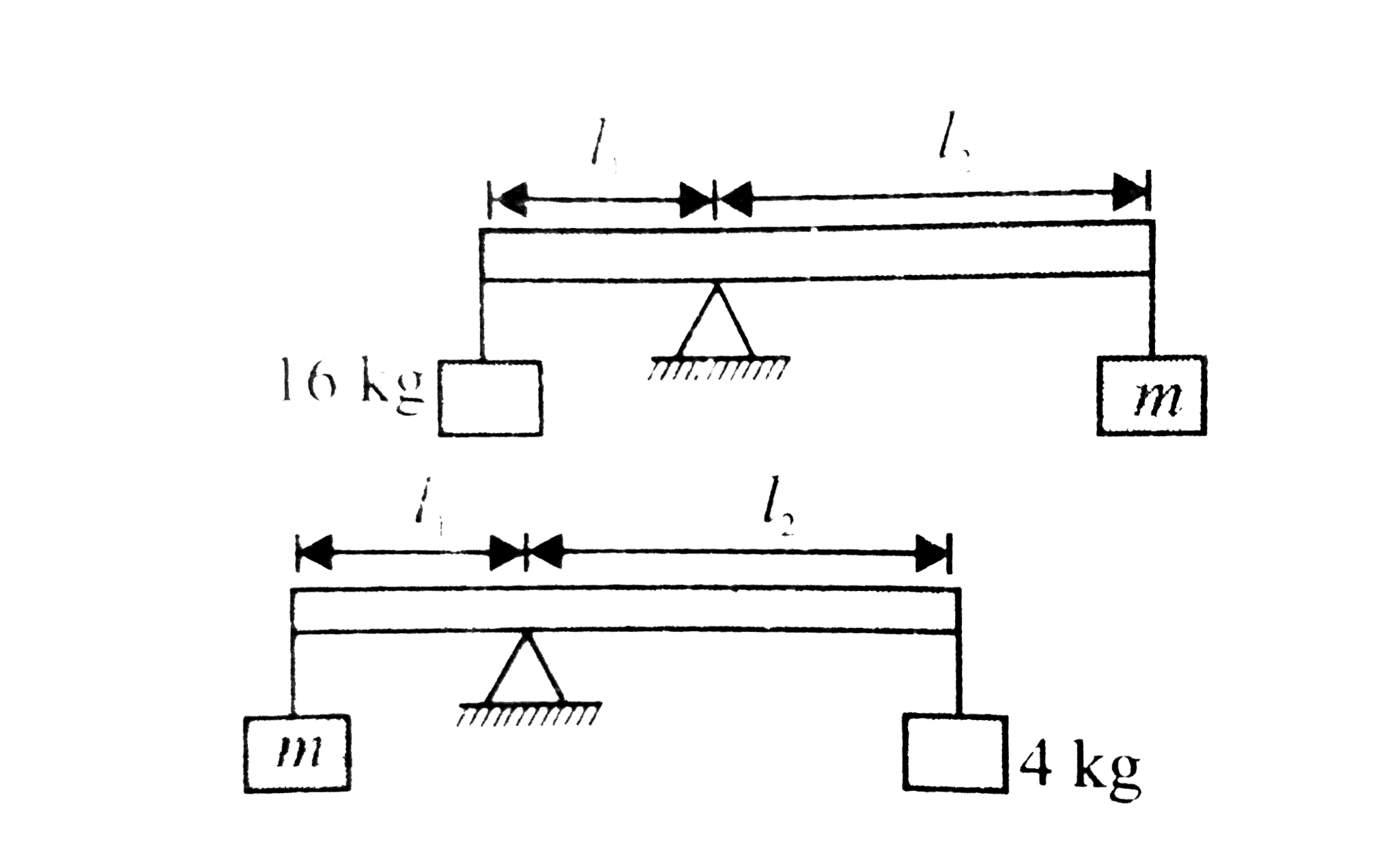 02:26View Solution
02:26View SolutionA sphere is moving towards the positive `x`-axis with a velocity `v_(c)` and rotates clockwise with angular speed `omega` shown in Fig. such that `v_(c)gtomegaR`. The instantaneous axis of rotation will be
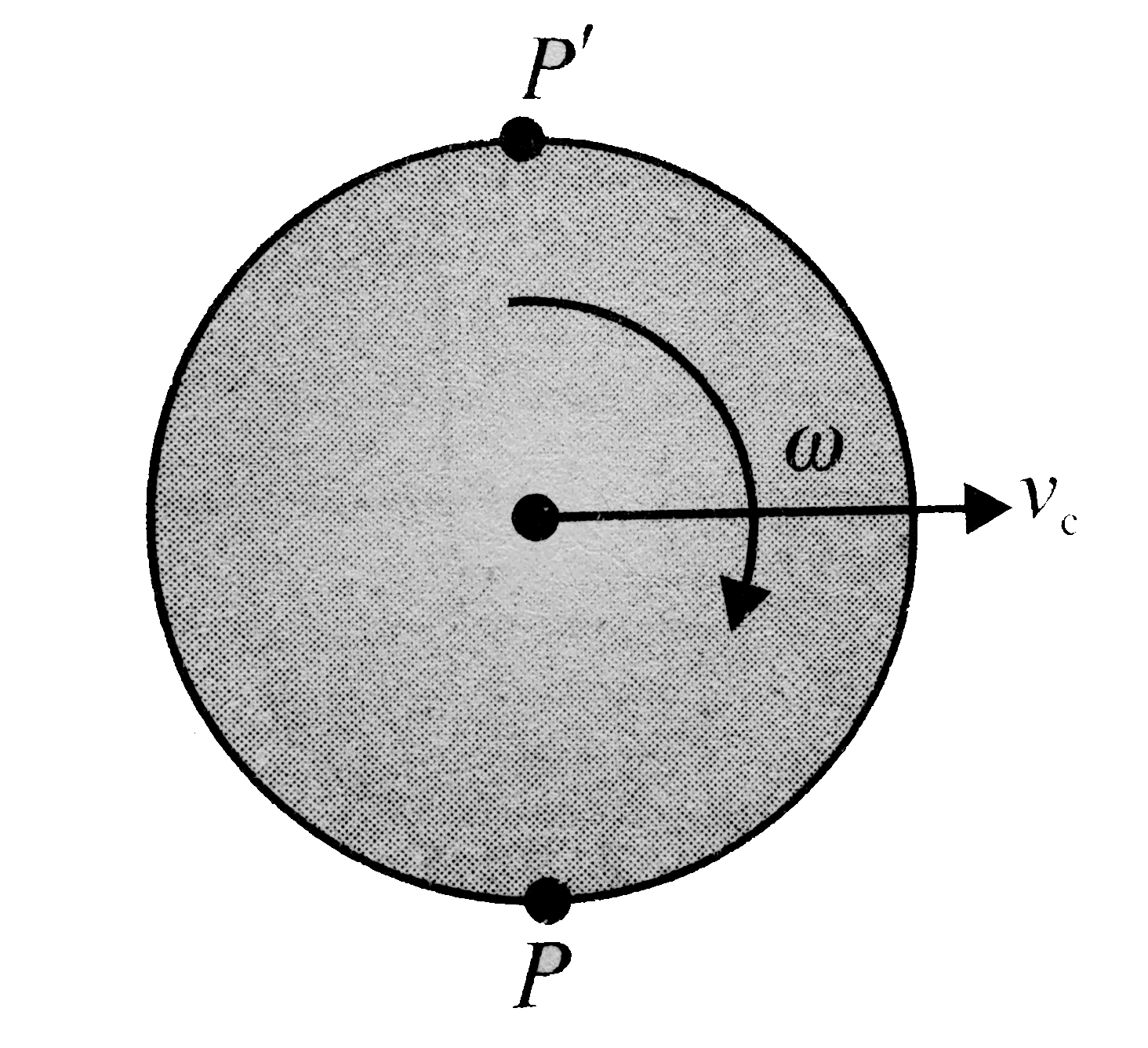 02:44View Solution
02:44View SolutionA cylinder of height `H` and diameter `H//4` is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is `2H` from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
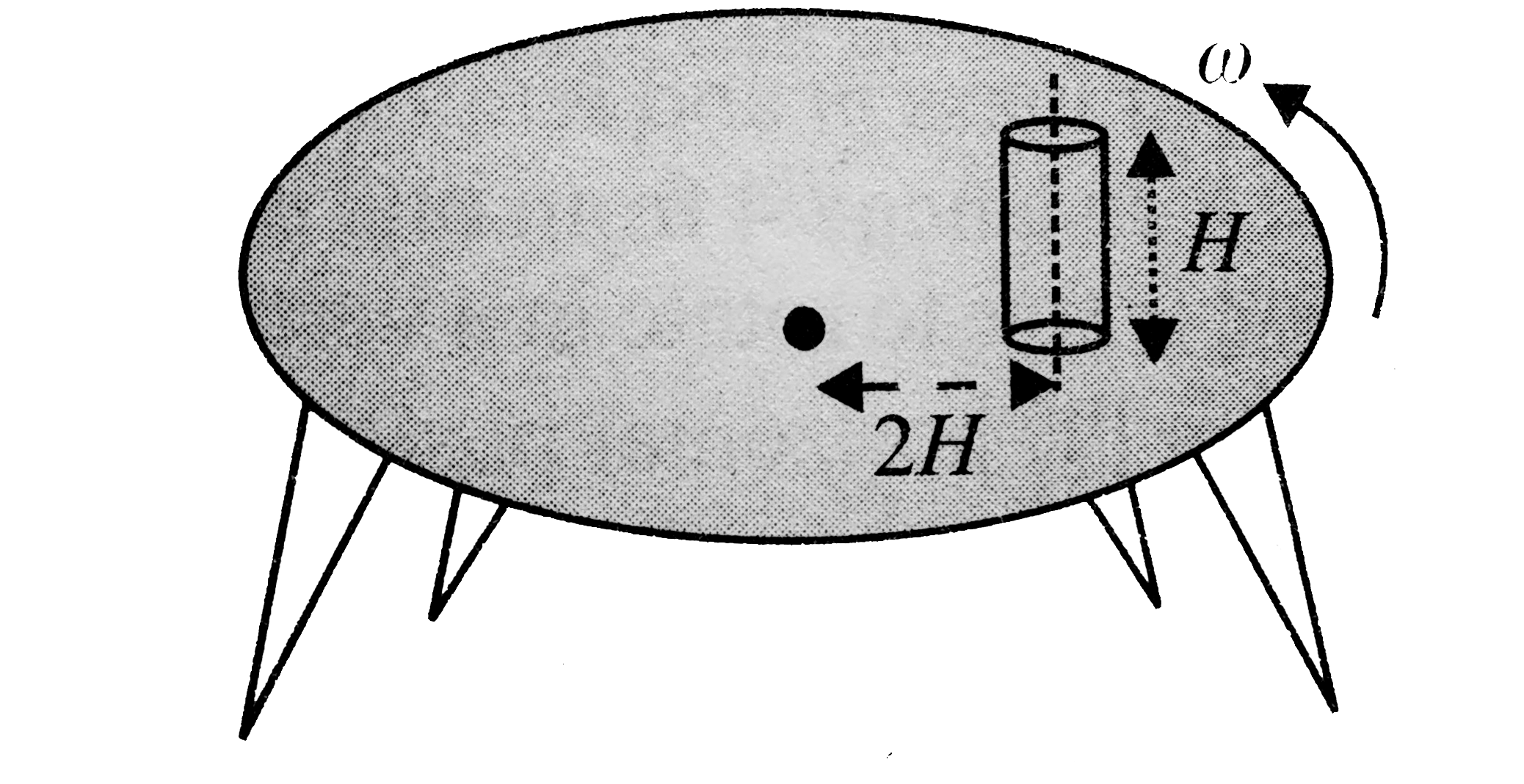 04:26View Solution
04:26View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?05:43View SolutionThree point masses `m_(1), m_(2)` and `m_(3)` are located at the vertices of an equilateral triangle of side `alpha`. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through `m_(1)?`
02:01View SolutionThe pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
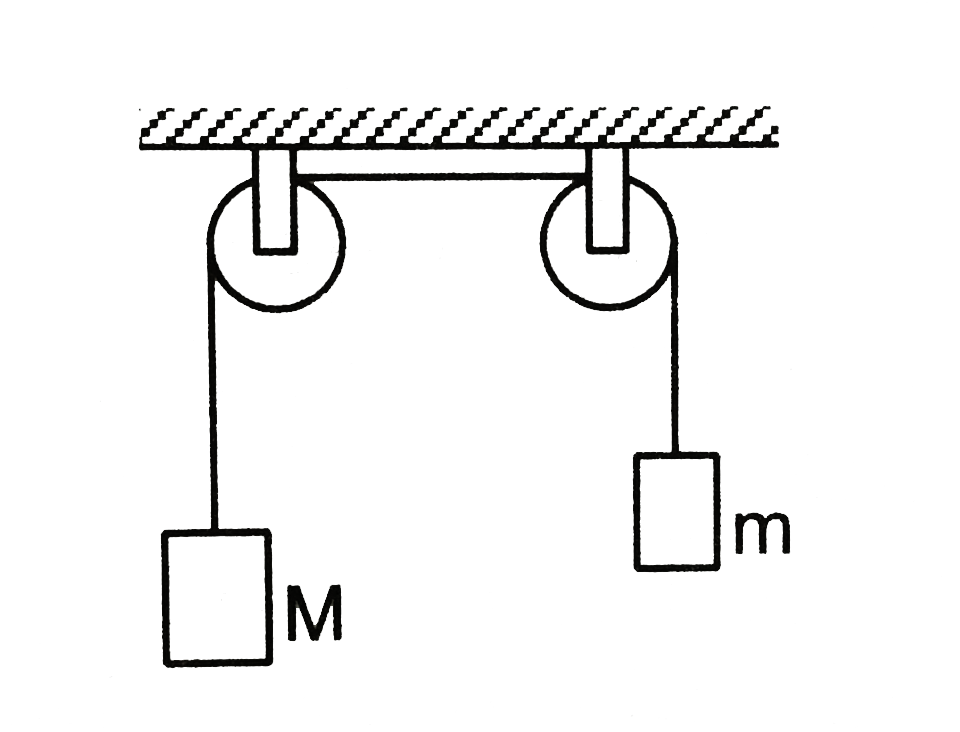 04:50View Solution
04:50View SolutionA uniform cube of side a and mass `m` rests on a rough horizontal table. A horizontal force `F` is applied normal to one of the faces at a point directly above the centre of the face, at a height `(3a)/(4)` above the base. What is the minimum value of `F` for which the cube begins to tip about an edge?
05:45View SolutionA ladder of length `l` and mass `m` is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is `mu`. The angle `theta` at which the ladder will stay in equilibrium is
03:49View SolutionA cube of side a is placed on an inclined plane of inclination `theta`. What is the maximum value of `theta` for which the cube will not topple?
 03:34View Solution
03:34View SolutionA uniform rod of length `l` is placed symmetrically on two walls as shown in Fig. The rod is in equilibrium. If `N_(1)` and `N_(2)` are the normal forces exerted by the walls on the rod, then
 01:58View Solution
01:58View SolutionA square plate of mass `M` and edge `L` is shown in the figure. The moment of inertia of the plate about the axis in the plane of plate and passing through one of its vertex making an angle `15^@` horizontal is `
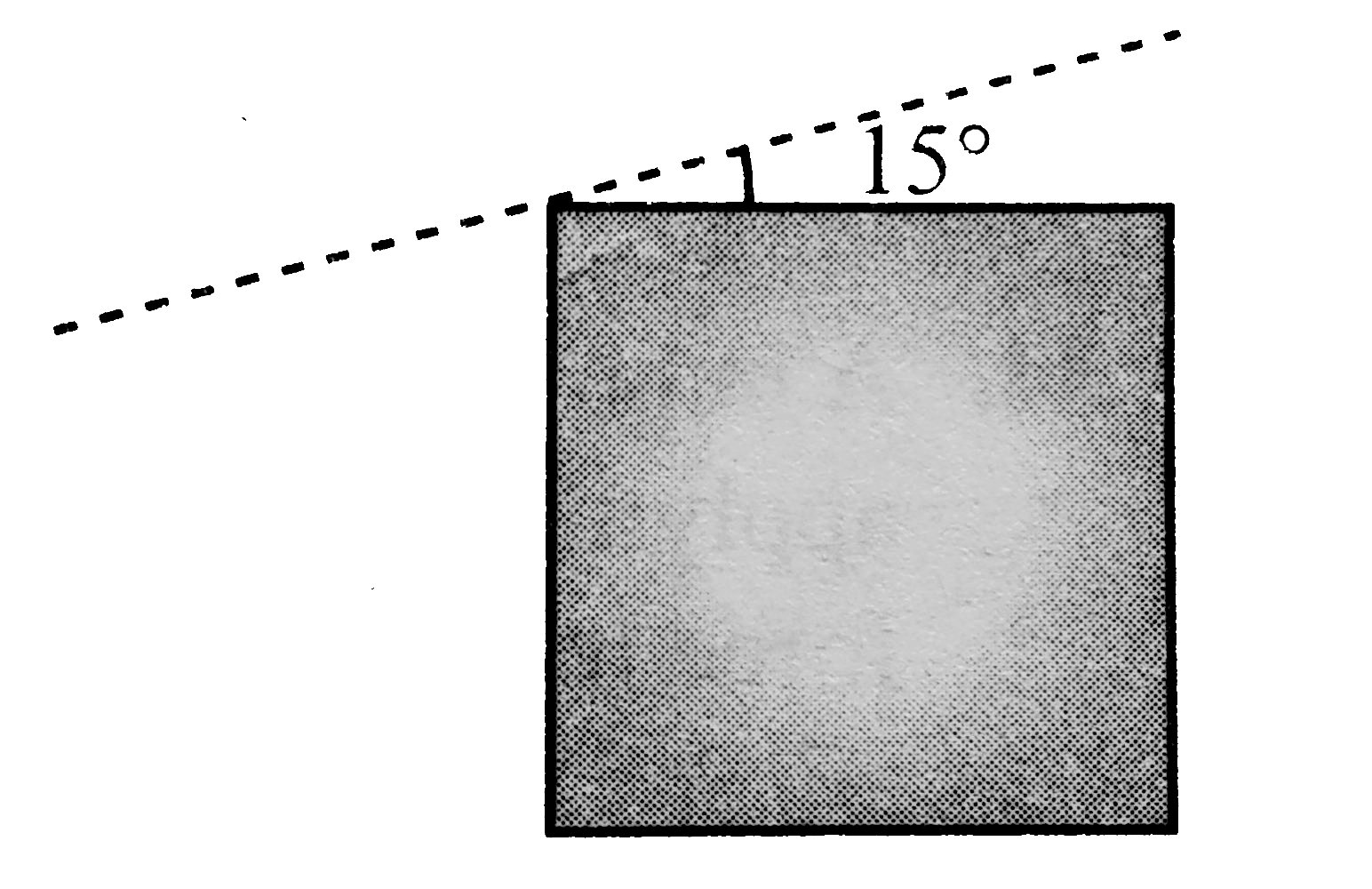 04:09View Solution
04:09View SolutionThe figure shows a uniform rod lying along the `x`-axis. The locus of all the points lying on the `x-y` plane, about which the moment of inertia of the rod is same as that about `O`, is
 04:06View Solution
04:06View SolutionFind minimum height of the obstacle so that the sphere can stay in equilibrium
 05:45View Solution
05:45View SolutionA sphere is placed rotating with its centre initially at rest in a corner as shown in Figs.(a) and (b). Coefficient of friction between all surfaces and the sphere is `1//3`. Find the ratio of the friction forces `f_(a)//f_(b)` by ground in situations (a) and (b).
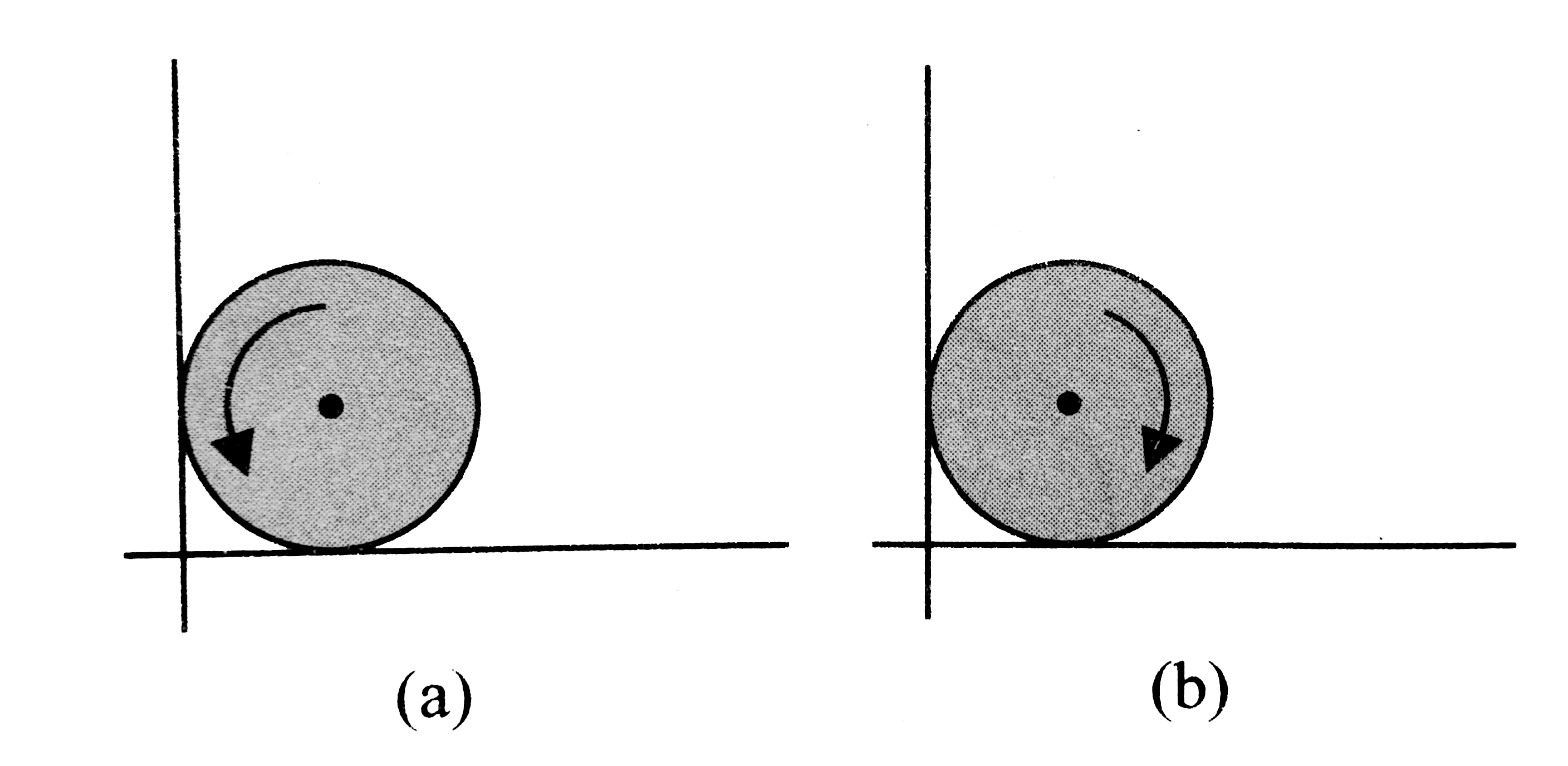 04:05View Solution
04:05View SolutionIn the figure shown, the instantaneous speed of end `A` of the rod is `v` to the left. The angular velocity of the rod of length `L` must be
 02:47View Solution
02:47View SolutionA uniform rod of mass `m` and length `l` is fixed from Point `A`, which is at a distance `l//4` from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?03:50View SolutionIn the pulley system shown, if radii of the bigger and smaller pulley are `2 m` and `1 m` respectively and the acceleration of block `A` is`5 m//s^2` in the downward direction, then the acceleration of block `B` will be :
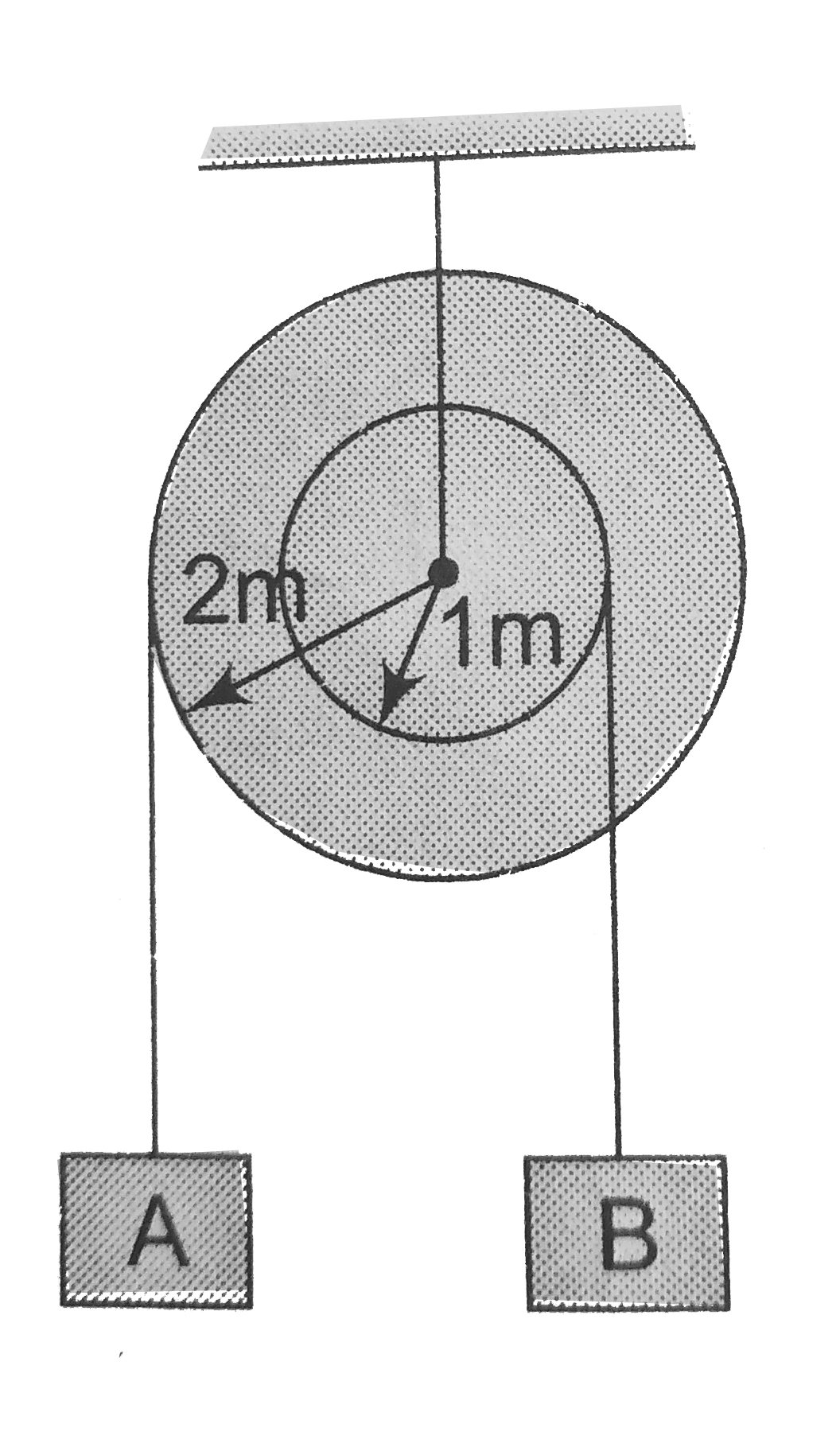 .01:31View Solution
.01:31View SolutionA planar object made up of a uniform square plate and four semicircular discs of the same thickness and material is being acted upon by four forces of equal magnitude as shown in Fig. The coordinates of point of application of forces is given by
 07:12View Solution
07:12View SolutionAn equilateral prism of mass `m` rests on a rough horizontal surface with coefficient of friction `mu`. A horizontal force `F` is applied on the prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is
 02:30View Solution
02:30View SolutionA uniform disc of radius `R` lies in the `x-y` plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line `y = x + c`. The value of `c` will be.
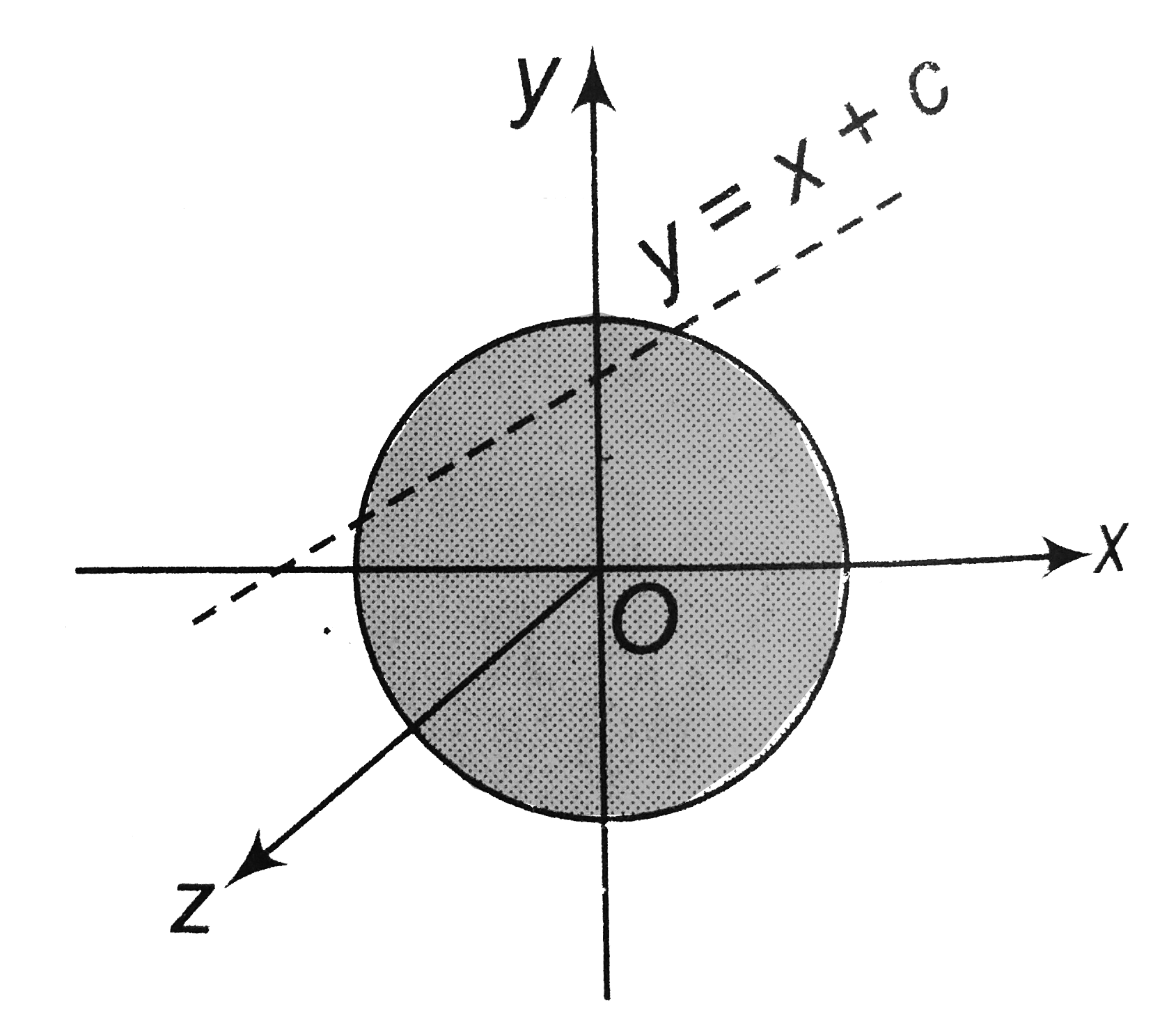 .06:51View Solution
.06:51View SolutionA rectangular block of mass `M` and height a is resting on a smooth level surface. A force `F` is applied to one corner as shown in Fig. At what point should a parallel force `3F` be applied in order that the block shall undergo pure translational motion? Assume normal contact force a between the block and surface passes through the centre of gravity of the block.
 02:08View Solution
02:08View SolutionA uniform rod of mass `15 kg` is held stationary with the help of a light string as shown in Fig. The tension in the string is
 02:11View Solution
02:11View SolutionFigure shown two pulley arrangments for lifting a mass `m` . In case-1, the mass is lifting by attaching a mass 2m while in case-2 the mass is lifted by pulling the other end with a downward force `F=2mg` . If `a_(a)` and `a_(b)` are the accelerations of the two masses then (Assumme string is massless and pulley is ideal).
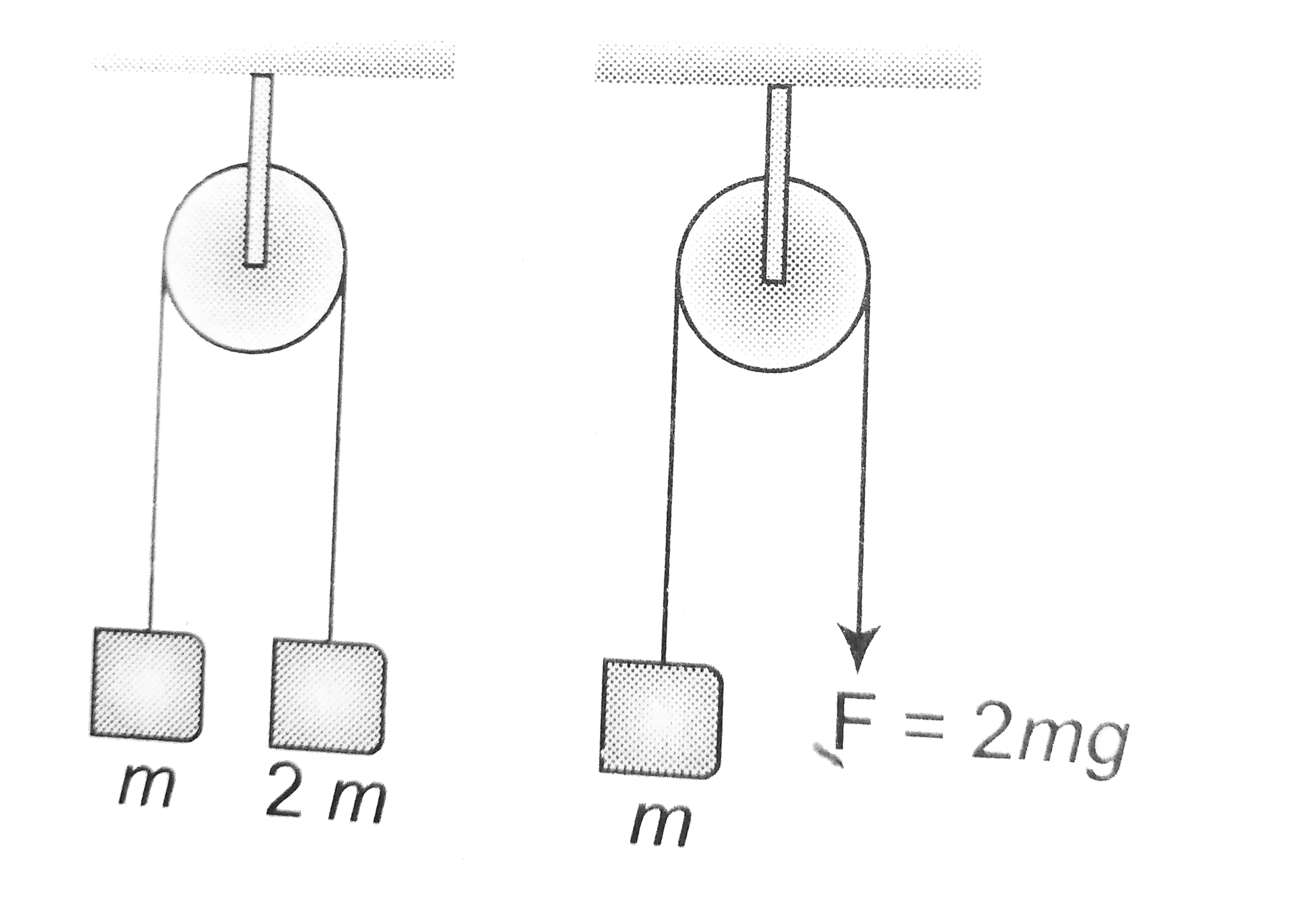 05:34View Solution
05:34View SolutionTwo uniform boards, tied together with the help of a string, are balanced on a surface as shown in Fig.
The coefficient of static friction between boards and surface is `0.5`. The minimum value of `theta`, for which this type of arrangement is possible is
 04:08View Solution
04:08View SolutionA slender rod of mass `m` and length `L` is pivoted about a horizontal axis through one end and released from rest at an angle of `30^@` above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is
 05:05View Solution
05:05View SolutionTwo painters are working from a wooden hoard `5 m` long suspended from the top of a building by two ropes attached to the ends of the plank. Either rope can withstand a maximum tension of `1040 N`. Painter `A` of mass `80 kg` is working at a distance of `1 m` from one end. Painter `B` of mass `60 kg` is working at a distance of `x` in from the centre of mass of the board on the other side. Take mass of the board as `20 kg` and `g = 10ms^(-2)`. The range of `x` so that both the painters can work safely is
View SolutionIn Fig. a massive rod `AB` is held in horizontal position by two massless strings. If the string at `B` breaks and if the horizontal acceleration of centre of mass, vertical acceleration and angular acceleration of rod about the centre of mass are `a_x,a_y` respectively, then
 View Solution
View SolutionA rod of length `L` is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle `37^@` with horizontal the velocity of `COM` of the rod of `2m//s`. The velocity of the end of the rod in contact with the surface at that instant is
02:41View SolutionA uniform bar `AB` of mass `m` and a ball of the same mass are released from rest from the same horizontal position. The bar is hinged at end `A`. There is gravity downwards. What is the distance of the point from point `B` that has the same acceleration as the ball, immediately after release?
 02:46View Solution
02:46View SolutionFind force F required to keep the system in equilibrium. The dimensions of the system are `d = 0.3 m` and `a = 0.2 m`. Assume the rods to be massless.
 01:50View Solution
01:50View SolutionA uniform cylinder of mass `m` lies on a fixed plane inclined at a angle `theta` with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass `m` hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of `m` is
 03:08View Solution
03:08View SolutionTwo blocks each of the mass `m` are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.
 02:27View Solution
02:27View SolutionA `198-cm` tall girl lies on a light (massless) board which is supported by two scales one under the top of her heal and one beneath the bottom of her feet. The two scales read respectively `36` and `30 kg`. What distance is the centre of gravity of this girl from the bottom of her feet? .
 02:03View Solution
02:03View SolutionThe wheels of an airplane are set into rotation just before landing so that the wheels do not slip on the ground. If the airplane is travelling in the east direction, what should be the direction of angular velocity vector of the wheels?
01:06View SolutionA wheel rotates with a constasnt acceleration of `2.0rad/s^2`. If the wheel starts from rest, how many evolutions wil it make in the first 10 senconds?
02:22View Solution
Uniform rod AB is hinged at end A in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Mass of block and rod is same and is equal to `m` Then acceleration of block just after release from this position is05:14View SolutionA 'T' shaped object with dimensions shown in the figure, is lying on a smooth floor. A force `'vecF'` is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect C.
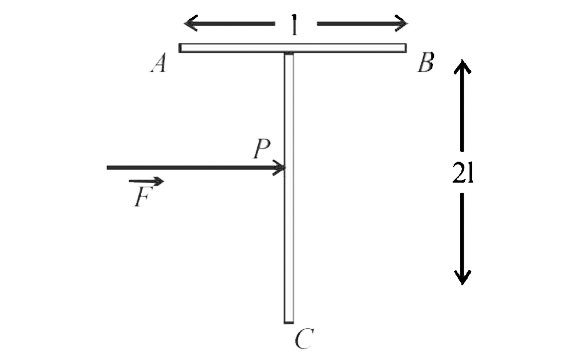 04:18View Solution
04:18View SolutionFour forces of the same magnitude act on a square as shown in figure. The square can rotate about point `O`, mid point of one of the edges. The force which can produce greatest torque is
 02:02View Solution
02:02View SolutionGiven a uniform disc of mass `M` and radius `R`. A small disc of radius `R//2` is cut from this disc in such a way that the distance between the centres of the two discs is `R//2`. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
04:28View SolutionA horizontal force `F` is applied at the top of an equilateral triangular block having mass `m`. The minimum coefficient of friction required to topple the block before translation will be
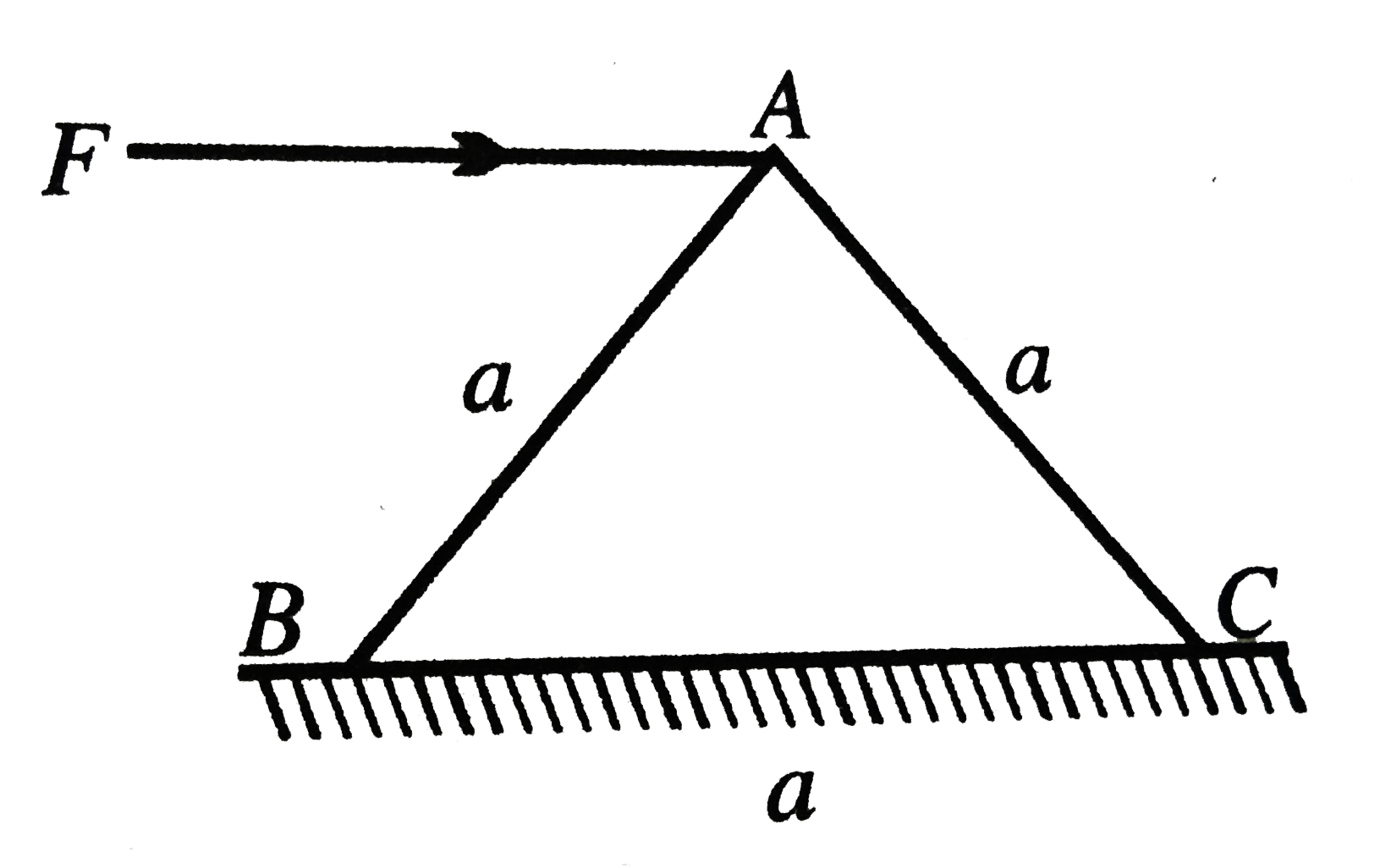 02:52View Solution
02:52View SolutionThe line of action of the resultant of two like parallel forces shifts by one-fourth of the distance between the forces when the two forces are interchanged. The ratio of the two forces is:
05:18View Solution`ABC` is a triangular plate of uniform `A` thickness. The sides are in the ratio shown in the figure. ` I_(AB), I_(BC), I_(CA)` are the moments of inertia of the plated about `AB, BC` and `CA` respectively. Which one of the following relation is correct?
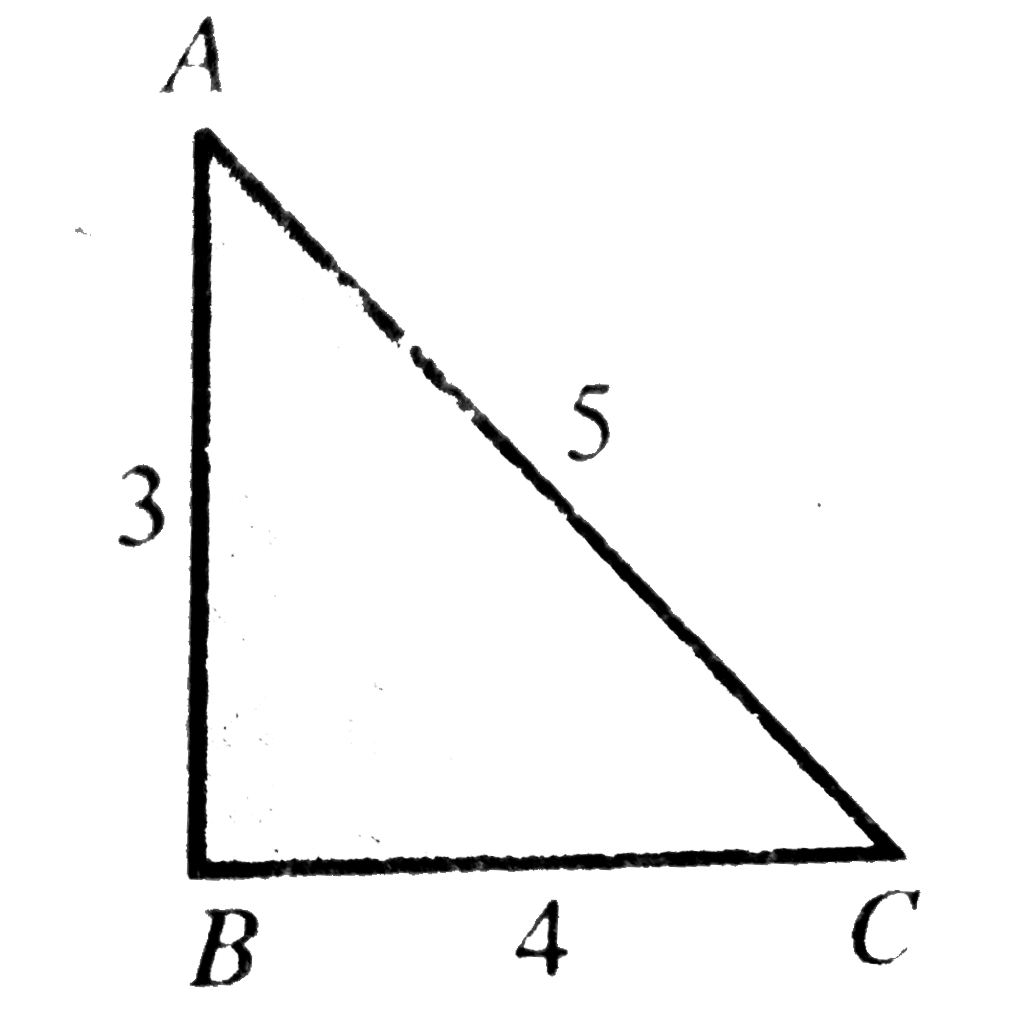 01:03View Solution
01:03View SolutionLer l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with AB. The moment of inertia of the plate about the axis CD is then equal to
01:26View SolutionIn a rectangle `ABCD, AB = 21` and `BC = 1`. Axes `xx` and `yy` pass through centre of the rectangle. The moment of inertia is least about :
 .03:36View Solution
.03:36View SolutionA uniform thin rod is bent in the form of closed loop `ABCDEFA` as shown in the figure. The ratio of moment of inertia of the loop about `x`-axis to that about `y`-axis is
 07:25View Solution
07:25View SolutionFigure shows an arrangement of masses hanging from a ceiling. In equilibrium, each rod is horizontal, has negligible mass and extends three times as far to the right of the wire supporting it as to the left. If mass `m_(4)` is `48 kg` then mass `m_(1)` is equal to
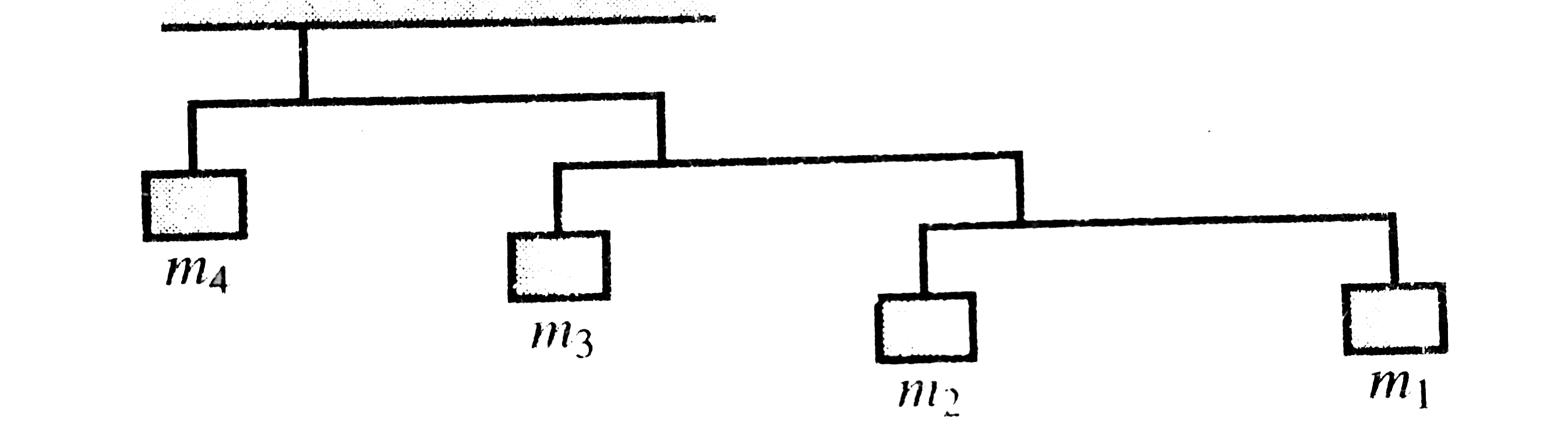 05:43View Solution
05:43View SolutionTwo identical uniform discs of mass `m` and radius `r` are arranged as shown in the figure. If `alpha` is the angular acceleration of the lower disc and `a_(cm)` is acceleration of centre of mass of the lower disc, then relation among `a_(cm), alpha` and `r` is
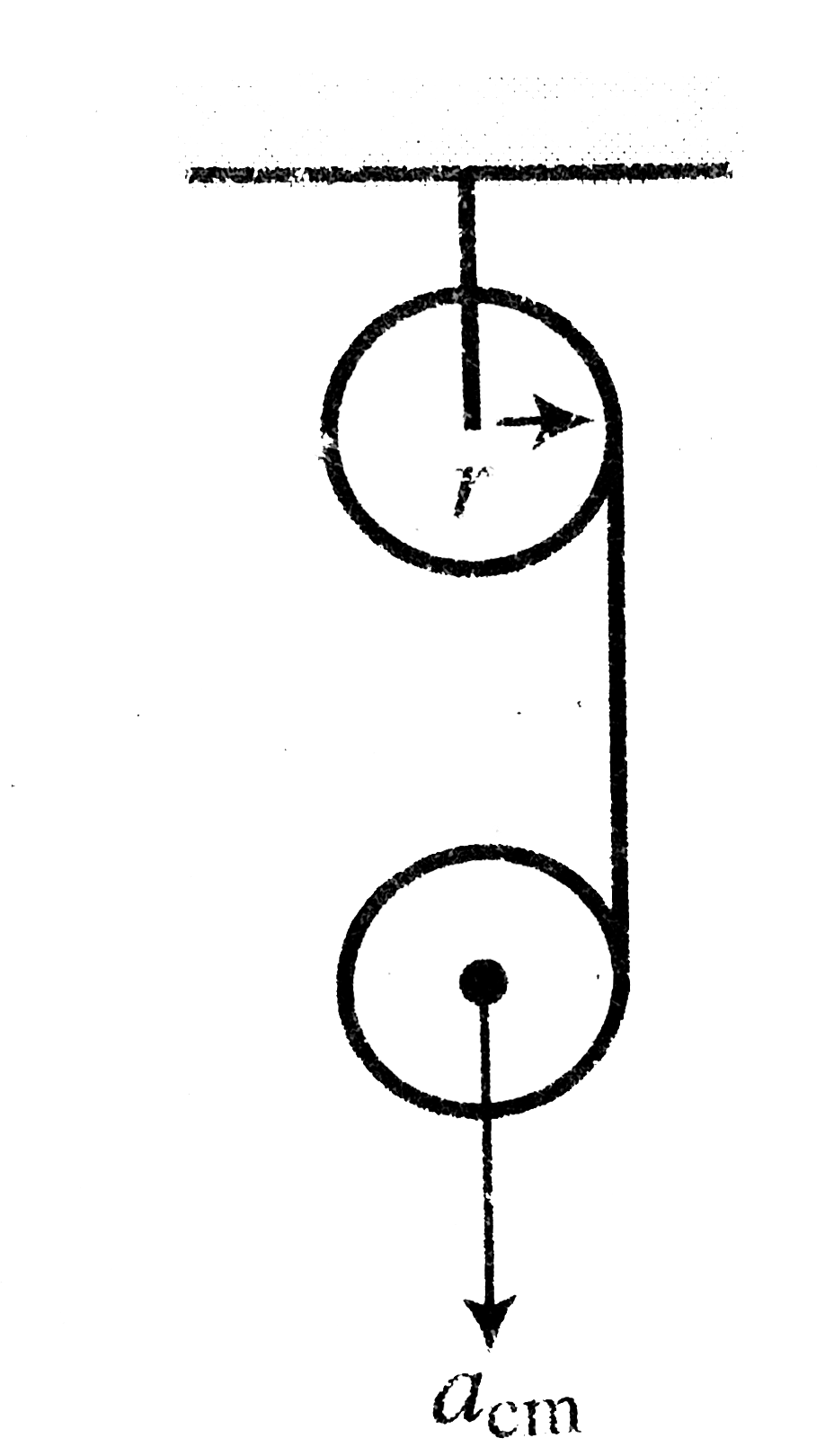 02:43View Solution
02:43View SolutionA uniform triangular plate `ABC` of moment of mass `m` and inertia `I` (about an axis passing through `A` and perpendicular to plane of the plate) can rotate freely in the vertical plane about point `'A'` as shown in figure. The plate is released from the position shown in the figure. Line `AB` is horizontal. The acceleration of centre of mass just after the release of plate is
 03:57View Solution
03:57View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
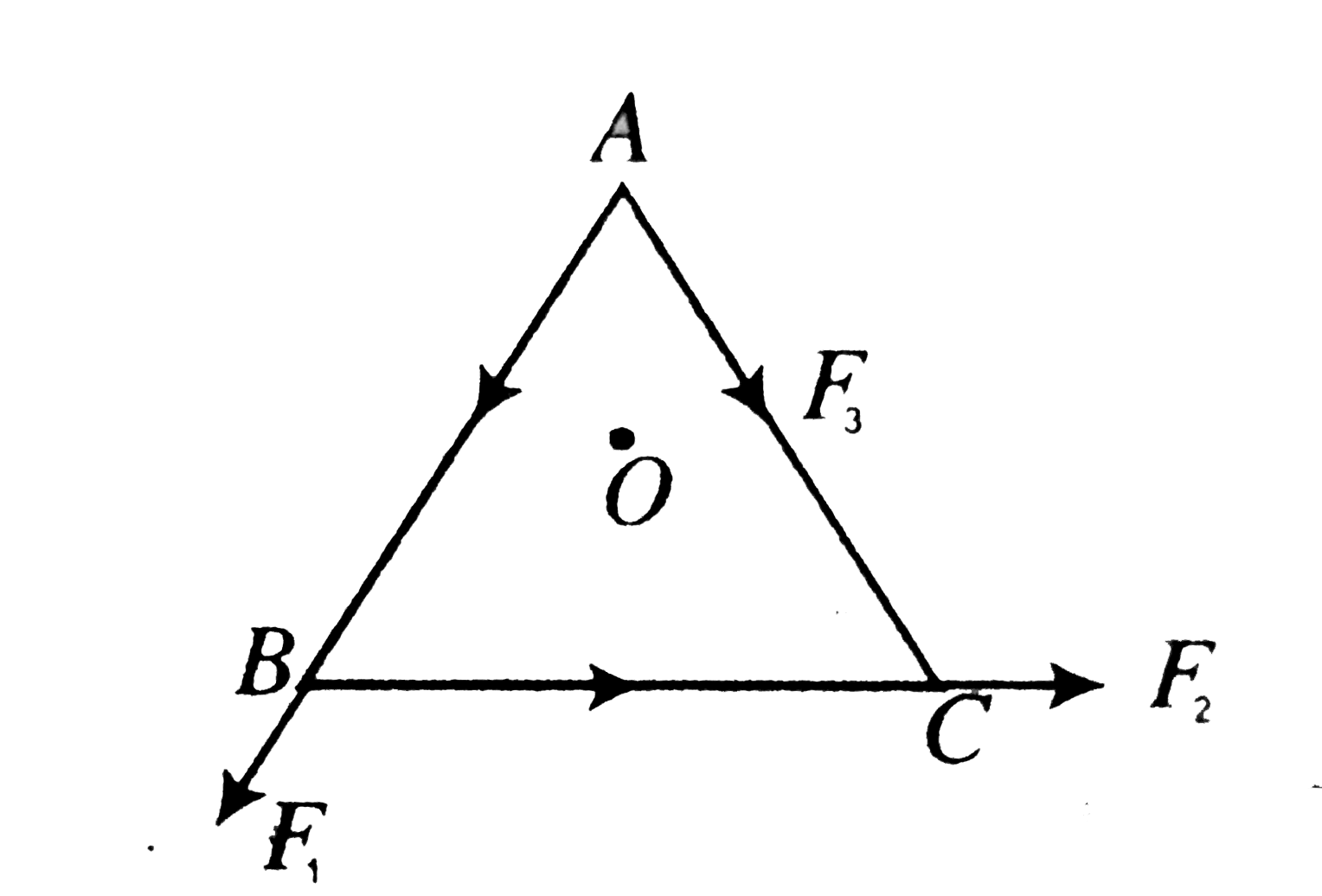 04:17View Solution
04:17View SolutionTwo discs have same mass and thickness. Their materials are of densities `pi` and `pi_(2)`. The ratio of their moment of inertia about central axis will be
02:44View SolutionLet `I_(A)` and `I_(B)` be moments of inertia of a body about two axes `A` and `B` respectively. The axis `A` passes through the centre of mass of the body but `B` does not
01:35View SolutionIn a rectangle `ABCD, AB = 21` and `BC = 1`. Axes `xx` and `yy` pass through centre of the rectangle. The moment of inertia is least about :
 .03:36View Solution
.03:36View SolutionFor the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
04:01View SolutionA uniform plane sheet of metal in the form of a triangle `ABC` has `BC gt AB gt AC`. Its moment of inertia will be smallest
02:02View SolutionThe masses of two uniform discs are in the ratio `1 : 2` and their diameters in the ratio `2 : 1`. The ratio of their moment, of inertia about the axis passing through their respective centres and perpendicular to their planes is
01:38View SolutionThere are four solid balls with their centres at the four comers of a square of side `a`. the mass of each sphere is `m` and radius is `r`. Find the moment of inertia of the system about (i) one of the sides of the square (ii) one of the diagonals of the square.
07:32View Solutionif `l_(1)` is te moment of inertia of a thin rod about an axis perpendicular to its length and passing thorugh its centre of mass and `l_(2)` te moment of inertia of the ring formed by the same rod about an axis passing through the centre of mass of the ring and perpendicular tot he plane of the ring. then find the ratio `(l_(1))/(l_(2))`.
01:55View SolutionMoment of inertia of a uniform rod of length `L` and mass `M`, about an axis passing through `L//4` from one end and perpendicular to its length is
02:24View SolutionA small hole is made in a disc of mass `M` and radius `R` at a distance `R//4` from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
01:23View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
01:31View SolutionWe have two spheres, one of which is hollow and the other solid. They have identical masses and moment of intertia about their respective diameters. The ratio of their radius is given by.
01:23View SolutionLet `I_(A)` and `I_(B)` be moments of inertia of a body about two axes `A` and `B` respectively. The axis `A` passes through the centre of mass of the body but `B` does not
View SolutionA triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to the plane of the paper and
(i) passing through `A`,
(ii) passing through `B`, by the application of some force `F` at `C` (mid - point AB) as shown in the figure. In which case angular acceleration is more ?
 .01:43View Solution
.01:43View SolutionTwo identical masses are connected to a horizontal thin massless rod as shown in the figure. When their distance from the pivot is `x`, a torque produces an angular acceleration `alpha_(1)`. If the masses are now repositioned so that they are at distance `2x` each from the pivot, the same torque will produce an angular acceleration `alpha_(2)` such that ,
 02:01View Solution
02:01View SolutionFrom a complete ring of mass `M` and radius `R`, a `30^@`sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,01:25View Solution
,01:25View SolutionA cubical block of side L rests on a rough horizontal surface with coefficient of friction `mu`. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 04:31View Solution
04:31View SolutionThe density of a rod continuously increases from `A` to `B`. It is easier to set it into rotation by
View SolutionThree children are sitting on a see-saw in such a way that is balances. A `20 kg` and a `30 kg` boy are on opposite sides at a distance of `2m` from the pivot. It the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is: (Neglect weight of board)
02:55View SolutionA wheel of radius `R` has an axle of radius `R//5`. A force `F` is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force `F'` is applied tangentially to the axle. The value of `F'` is
02:16View SolutionCalculate the force `F` that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height `0.4 m`. Radius of wheel is `1m` and `mass = 10 kg` . `F` is
 02:37View Solution
02:37View SolutionA rigid body is rotating about a vertical axis. In `t` second, the axis gradually becomes horizontal. But the rigid body continues to make `v` rotations per second throughout the time interval of `1` second. If the moment of inertia `I` of the body about the axis of rotation can he taken as constant, then the torque acting on the body is
03:03View SolutionA string is wrapped around a cylinder of mass `M` and radius `R`. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
04:25View SolutionEnd `A` of the bar `AB` in figure rests on a frictionless horizontal surface and end `B` is hinged. A horizontal force `vecF` of magnitude `120 N` is exerted on end `A`. You can ignore the weight of the bar. What is the net force exerted by the bar on the hinge at `B`?
 04:49View Solution
04:49View Solution
Single Correct questions and complete solutions for chapter RIGID BODY DYNAMICS 1 of CENGAGE PHYSICS (HINGLISH) of Class 11
