Complete Solutions to Illustration of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
The time period of jupiter is 11-6 year, how far is jupitor from the sun. Distance of earth from the sun is `1.5 xx 10^(11) m`.
View SolutionThe mean distance of Mars from the sun in `1.524` times that of the Earth from the sun. Find the number of years requires for Mars make one revolution about the Sun.
View SolutionLet the speed of the planet at the perihelion `P` in figure be `v_(P)` and the Sun planet distance `SP` be `r_(P)`. Relater `r_(P), v_(P)` to the corresponding quantities at the aphelion `(r_(A),v_(A))`. Will the planet take equal times to transverse `BAC` and `CPB`?

View SolutionA sphere of mass `40 kg` is attracted by a second sphere of mass `15 kg`, when their centres are `20 cm` apart, with a force of `0.1` miligram weight. Caculate the value of gravitational constant.
View SolutionThe mass of planet Jupiter is `1.9xx10^(7)kg` and that of the Sun is `1.9x10^(30)kg`. The mean distance of Jupiter from the Sun is `7.8xx10^(11)`m. Calculate te gravitational force which Sun exerts on Jupiter. Assuming that Jupiter moves in circular orbit around the Sun, also calculate the speed of Jupiter `G=6.67xx10^(-11)Nm^(2)kg^(-2)`.
View SolutionGravitational force between two point masses `m` and `M` separated by a distance `r` is `F`. Now if a point mass `3m` is placed next to `m`, what will be that a. force on `M` due to `m`, b total on `M`?
View SolutionTwo particles of masses `m_(1)` and `m_(2)` initially at rest a infinite distance from each other, move under the action of mutual gravitational pull. Show that at any instant therir relative velocity of approach is `sqrt(2G(m_(1)+m_(2))//R)` where `R` is their separation at that instant.
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m

View SolutionThree particles, each of mass m, are situated at the vertices of equilateral triangle of side length a. The only forces. It is desired that each particle moves in a circle while maintaining the original mutual speration a. Find the intial velocity that should be given to each particle and also the time period of the circular motion.
View SolutionFigure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was `M`. With what gravitational force does the hollowed out lead sphere attract a particle of mass `m` that lies at a distance `d` from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
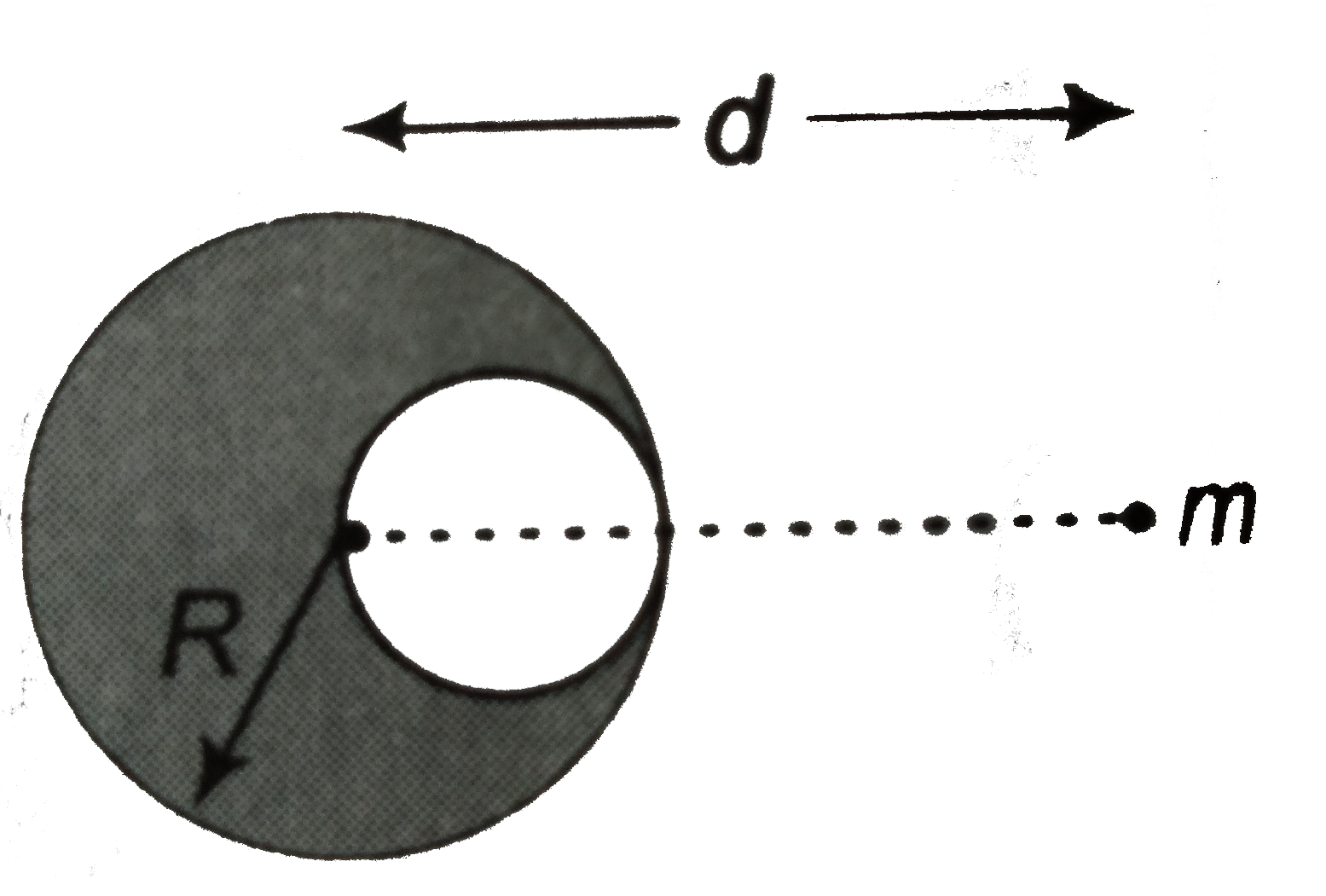
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionIn a double star, two stars (one of mass `m` and the other of mass `2m`) distance `d` apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.
View SolutionFind the relation between the gravitational field on the surface of two planets `A` and `B` of masses `m_(A), m_(B)` and radii `R_(A)` and `R_(B), `respectively if
a. they have equal mass.
b. they have equal (uniform)density.
View SolutionCalculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass `M` and radius `R`. (Assume the base of hemisphere to be open)

View SolutionTwo masses `90 kg` and `160 kg` are at a distance `5 m` apart. Compute the magnitude of intensity of the gravitational field at a point distance `3 m` from the `90 kg` and `4m` from the `160 kg` mass. `G=6.67xx10^(-11)kg^(-2)`
View SolutionTwo bodies of masses `100 kg` and `10,000 kg` are at a distance `1m` part. At which point on the line joining them will the resultant gravitational field intensity be zero?
View SolutionAssuming the earth of to be a uniform sphere of radius `6400 kg` and density `5.5 g//c.c.`, find the value of `g` on its surface`G=6.66xx10^(-11)Nm^(2)kg^(-2)`
View SolutionAt what height from the surface of earth will the value of g be reduced by `36%` from the value on the surface? Take radius of earth `R = 6400 km`.
View SolutionFind the percentage decrease in the weight of the body when taken to a depth of `32 km` below the surface of earth. Radius of the earth is `6400 km`.
View SolutionWhat is the fractional decrease in the value of free-fall acceleration g for a particle when it is lifted from the surface to an elevation `h`? `(h lt lt R)`
View Solutiona. Find the height from the earth's surface where `g` will be `25%` of its value on the surface of earth `(R=6400km)`. b. Find the percentage increase in the value of `g` at a depth `h` from the surface of earth.
View SolutionWhat would be the time period of rotation of earth so that the bodies at the equator would weight `40%` of their actual weight?
View SolutionOn a planet whose size is the same and mass four times as that of our earth, find the amount of work done to lift `3 kg` mass vertically upwards through `3 m` distance on the planet. The value of `g` on the surface of earth is `10 ms^(-2)`
View SolutionThe gravitational field in a region is given by `vecE=-(20Nkg^(-1))(hati+hatj)`. Find the gravitational potential at the origin `(0,0)` in `J kg^(-1)`
View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass `m`, radius `R`
View SolutionA particle of mass 'm' is raised to a height `h = R` from the surface of earth. Find increase in potential energy. `R =` radius of earth. `g =` acceleration due to gravity on the surface of earth.
View SolutionThe gravitational potential difference between the surface of a planet and a point `20 m` above it is `16 J//kg`. Calculate the work done in moving a `4 kg` body by `8m` on a slope of `60^@` from the horizontal.
View SolutionA projectile is fired vertically from the earth's surface with an initial speed of `10 km//s`. Neglecting air drag, how high above the surface of earth will it go?
View SolutionA satellite of mass `1000 kg` is rotating around the earth in a circular orbit of radius `3R`. What extra energy should be given to this catellite if it is to be lifted into an orbit of radius `4R`?
View SolutionTwo particles of masses `m` and `M` are initially at rest at an infinite distance part. They move towards each other and gain speeds due to gravitational attracton. Find their speeds when the separation between the masses becomes equal to `d`.
View SolutionA body is released at a distance far away from the surface of the earth. Calculate its speed when it is near the surface of earth. Given `g=9.8ms^(-2)` radius of earth `R=6.37xx10^(6)m`
View SolutionCalculate the velocity with which a body must be thrown vertically from the surface of the earth so that it may reach a height of `10R`, where `R` is the radus of the earth and is equal to `6.4xx10^(8)m`. (earth's mass`=6xx10^(24)kg`, gravitational constant `G=6.7xx10^(-11)Nm^(2)kg^(-2))`
View SolutionDistance between the centres of two stars is `10a`. The masses of these stars are `M` and `16 M` and their radii `a` and `2a` respectively. A body of mass `m` is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of `G`, `M` and `a`.
View SolutionEstimate whether it takes more energy to get a satellite upto `1600 km` above the earth than to put in orbit there. Earth's radius is `6400 km`. Does your answer remain same for height `3200 km` or for height `4800 km`?
View SolutionCalculate the self-gravitational potential energy of matter forming a. a thin uniform shell of mass `M` and radius `R`, b. a uniform sphere of mass `m` and radius `R`.
View SolutionCalculate the escape speed on the surface of a planet of mass `7.5xx10^(25)g`, and radius `1.6xx10^(8)cm. G=6.67xx10^(-8)"dyne"cm^(2)g^(-2)`.
View SolutionThe escape speed from earth's surface is `11kms^(-1)`. A certain planet has a radius twice that of earth but its mean density is the same as that of the earth. Find the value of the escape speed from the planet.
View SolutionA spaceship is launched into a circular orbit close to the earth's surface . What additional velocity has now to be imparted to the spaceship in the orbit to overcome the gravitational pull. Radius of earth `= 6400 km`, `g = 9.8m//s^(2)`.
View SolutionA rocket starts vertically upward with speed `v_(0)`. Show that its speed `v` at height `h` is given by `v_(0)^(2)-v^(2)=(2hg)/(1+h/R)`
where `R` is the radius of the earth and `g` is acceleration due to gravity at earth's suface. Deduce an expression for maximum height reachhed by a rocket fired with speed `0.9` times the escape velocity.
View SolutionFor a particle projected in a transverse direction from a height `h` above earth's surface, find te minimum initial velocity so that it just grazes the surface of earth such that path of this particle would be an ellipse with centre of earth as the farther focus, point of projection as the apogee and a diametrically opposite point on earth's surface as perigee.
View SolutionTwo masses `m_(1)` and `m_(2)` at an infinite distance from each other are initially at rest, start interacting gravitationally. Find their velocity of approach when they are at a distance `r` apart.
View SolutionAn artificial satellite revolves round the earth at a height of `1000 km`. The radius of the earth is `6.38xx10^(3)km`. Mass of the earth `6xx10^(24)kg,G=6.67xx10^(-11)Nm^(2)kg^(-2)`. Find the orbital speed and period of revolution of the satellite.
View SolutionA satellite orbits the earth at a height of `3.6xx10^(6)m` from its surface. Compute it’s a kinetic energy, b. potential energy, c. total energy. Mass of the satellite `=500kg` mass of the earth `=6xx10^(24)`kg, radius of the earth `=6.4xx10^(6), G=6.67xx10^(-11)Nm^(2)kg^(-2)`.
View SolutionYou are given the following data `:g=9.81ms^(-2)`, radius of earth `=6.37xx10^(6)m` the distance the Moon from the earth `=3.84xx10^(8) m` and the time period of the Moon's revolution `=27.3days`. Obtain the mass of the earth in two different ways. `G=6.67xx10^(-11)Nm^(2)kg^(2)`.
View SolutionAssume the radius of the earth to be `6.4xx10^(6)m`
a. Calculate the time period `T` of a satellite on equational orbit at `1.4xx10^(e)m` above the surface of the earth.
b. What is the speed of the satellite in this orbit?
c. If the satellite is travelling in the same direction as the rotation of the earth i.e. west to east, what is the interval between two successie times at which it will appear vertically overhead to an observed at a fixed point on the equator?
View SolutionTwo satellites `A` and `B` of equal mass move in the equatorial plane of the earth, close to earth's surface. Satellite `A` moves in the same direction as the of the rotation of the earth while satellite `B` moves in the opposite direction. Calclate the ratio of the kinetic energy of `B` of that of `A` in the reference frame fixed to the earth `(g=9.8ms^(-2)` and radius of the earth `=6.37xx10^(6)km)`
View SolutionA satellite is revolving in the circular equatorial orbit of radius `R=2xx10^(4)km` from east to west. Calculate the interval after which it will appear at the same equatorial town. Given that the radius of the earth `=6400km` and `g` (acceleration due to gravity) `=10ms^(-2)`
View SolutionA satellite ils launched into a circular orbit `1600km` above the surface of the earth. Find the period of revolution if the radius of the earth is `R=6400km` and the acceleration due to gravity is `9.8ms^(-2)`. At what height from the ground should it be launched so that it may appear stationary over a point on the earth's equator?
View Solution
Illustration questions and complete solutions for chapter GRAVITATION of CENGAGE PHYSICS (HINGLISH) of Class 11