Complete Solutions to Subjective of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| CENGAGE PHYSICS | Subjective |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Calculate the velocity with which a body must be thrown vertically upward from the surface of the earth so that it may reach a height of `10R`, where `R` is the radius of the earth and is equal to `6.4 xx 10^(6)m.` (Given: Mass of the earth `= 6 xx 10^(24) kg`, gravitational constant `G = 6.7 xx 10^(-11) N m^(2) kg^(-2)`)
View SolutionA sky laboratory of mass `2 xx 10^(3) kg` has to be lifted from one circular orbit of radius `2R` into another circular orbit of radius `3R`. Calculate the minimum energy required if the radius of earth is `R= 6.37 xx 10^(6) m` and `g= 9.8 ms^(-2)`
View SolutionEstimate whether it takes more energy to get a satellite upto `1600 km` above the earth than to put in orbit there. Earth's radius is `6400 km`. Does your answer remain same for height `3200 km` or for height `4800 km`?
View SolutionThe gravitational field in a region is given by `vecE = (3hati- 4hatj) N kg^(-1)`. Find out the work done (in joule) in displacing a particle by `1 m` along the line `4y = 3x + 9`.
View SolutionA body suspended on a spring balance in a ship weighs `W_(0)` when the ship is at rest. When the ship begins to move along the equator with a speed `v`, show that the scale reading is very close to `W_(0) (1+-2omegaV//g`), where `omega` is the angular speed of the earth.
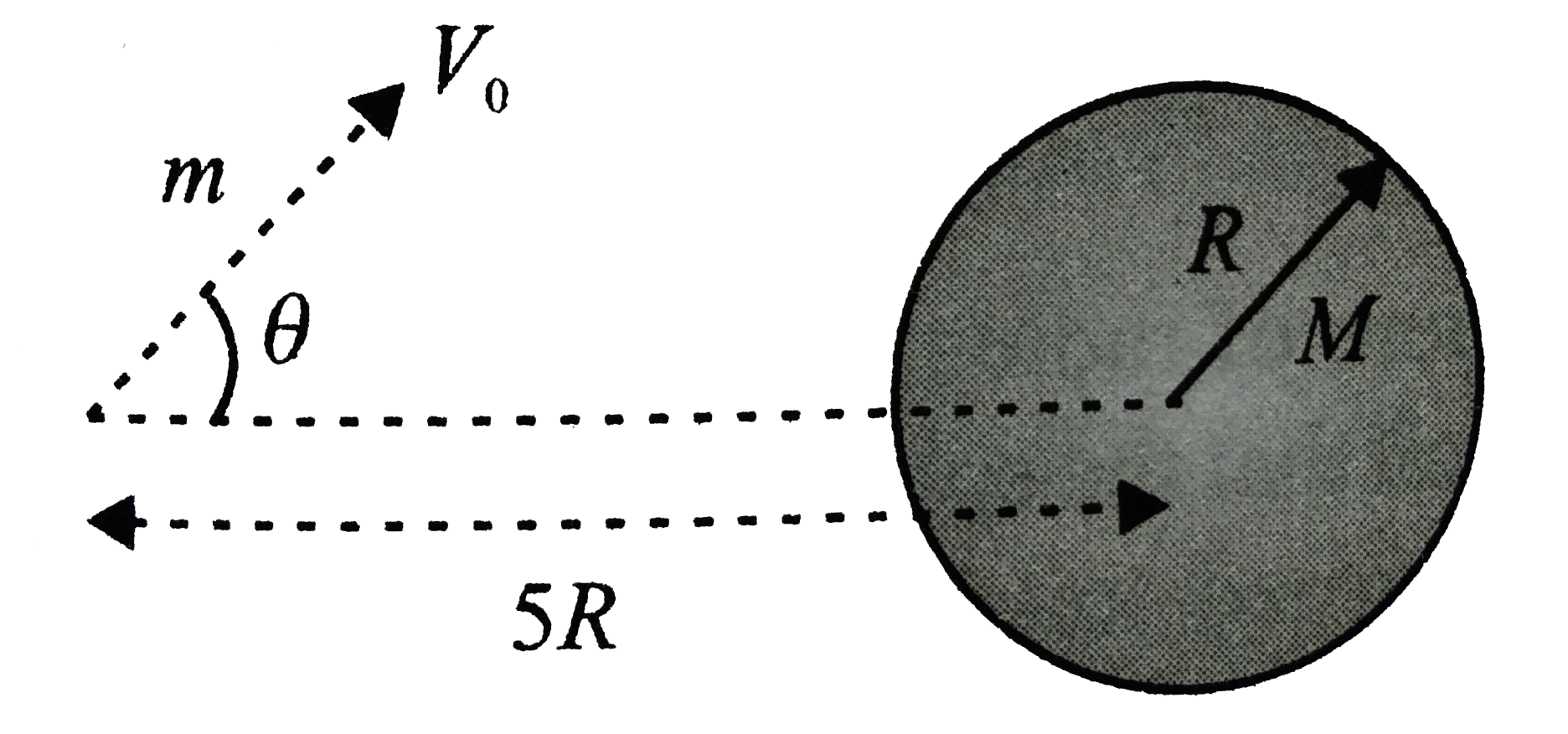
View SolutionA spaceship is sent to investigate a planet of mass `M` and radius `R`. While hanging motionless in space at a distance `5R` from the centre of the planet, the spaceship fires an instrument package of mass `m`, which is much smaller than the mass of the spaceship. For what angle `theta` will the package just graze the surface of the planet?
View SolutionRavi can throw a ball at a speed on the earth which can cross a river of width `10 m`. Ravi reaches on an imaginary planet whose mean density is twice that of the earth. Find out the maximum possible radius of the planet so that if Ravi throws the ball at the same speed it may escape from the planet. Given radius of the earth `= 6.4 xx 10^(6) m`.
View SolutionA spaceship approaches the Moon (mass `= M` and radius `= R` along a parabolic path which is almost tangential to its surface. At the moment of the maximum approach, the brake rocket is fired to convert the spaceship into a satellite of the Moon. Find the change in speed.
View SolutionTaking the earth to be a uniform sphere of radius `6400 km` and the value of g at the surface to be `10ms^(-2)`, calculate the energy needed to raise a satellite of mass `2000 kg` to a height of `800 km` a above the earth's surface and to set it into circular orbit at that altitude.
View SolutionA satellite is to be put into an orbit `600 km` above the surface of the earth. If its vertical velocity after launching is `2400 m//s` at this height, calculate the magnitude and direction in the impulse required to put the satellite directly increase. The mass of the satellite is `60 kg` and the radius of the earth is `6400 km`. Take `g=10 ms^(-2)`
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass `M` and the other `m`. Their centres are a distance `d` apart, `d` being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of `1` year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is `r` and the distance of the earth from the Sun is `R`, find the relation between `r` and `R`.
View SolutionA satellite revolving in a circular equatorial orbit of radius `R = 2.0 xx 10^(4)` km from west to east appears over a certain point at the equator every `11.6 h`. From these data, calculate the mass of the earth. `(G = 6.67 xx 10^(-11) N m^(2))`
View SolutionAn artificial satellite (mass m) of a planet (mass M) revolves in a circular orbit whose radius is n times the radius R of the planet in the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the force of resistance on satellite to depend on velocity as `F=av^(2)` where 'a' is a constant caculate how long the satellite will stay in the space before it falls on to the planet's surface.
View SolutionA satellite of mass `m` is orbiting the earth in a circular orbit of radius `r`. It starts losing energy due to small air resistance at the rate of `C J//s`. Then the time teken for the satellite to reach the earth is...........
View Solution
Subjective questions and complete solutions for chapter GRAVITATION of CENGAGE PHYSICS (HINGLISH) of Class 11