Complete Solutions to Single Correct of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The escape velocity for a body projected vertically upwards from the surface of the earth is `11.2 km s^(-1)`. If the body is projected in a direction making an angle `45^@` with the vertical, the escape velocity will be
View SolutionA projectile is fired from the surface of earth of radius `R` with a velocity `k upsilon_(e)` (where `upsilon_(e)` is the escape velocity from surface of earth and `k lt 1)`. Neglecting air resistance, the maximum height of rise from centre of earth is
View SolutionThe radius of a planet is `R`. A satellite revolves around it in a circle of radius `r` with angular velocity `omega_(0)`. The acceleration due to the gravity on planet's surface is
View SolutionA space vehicle approaching a planet has a speed v when it is very far from the planet At that moment tangent of its trajectory would miss the centre of the planet by distance R if the planet has mass M and radius r what is the smallest value of R in order that the resulting orbit of the space vehicle will just miss the surface of the planet?
View SolutionThe planets with radii `R_(1)` and `R_(2)` have densities `p_(1),p_(2)` respectively. Their atmospheric pressues are `p_(1)` and `p_(2)` respectively.Therefore, the ratio of masses of their atmospheres, neglecting variation of g within the limits of atmoshpere is
View SolutionA particle of mass 'm' is raised to a height `h = R` from the surface of earth. Find increase in potential energy. `R =` radius of earth. `g =` acceleration due to gravity on the surface of earth.
View SolutionA space station is set up in space at a distance equal to the earth's radius from the surface of the earth. Suppose a satellite can be launched from the space station. Let `v_(1)` and `v_(2)` be the escape velocities of the satellite on the earth's surface and space station, respectively. Then
View SolutionThe orbital velocity of an satellite in a circular orbit just above the earth's surface is `v`. For a satellite orbiting at an altitude of half of the earth's radius, the orbital velocity is
View SolutionThe radius of earth is about `6400Km` and that of mars is about `3200 km` The mass of the earth is about `10`times the mass of mars. An object weight `200N` on earth 's surface, then its weight on the surface of mars will be:
View SolutionThe distance of the two planets from the Sun are `10^(13)m` and `10^(12) m`, respectively. Find the ratio of time periods and speeds of the two planets.
View SolutionThe gravitational force between two objects is proportional to `1//R` (and not as `1//R^(2)`) where `R` is separation between them, then a particle in circular orbit under such a force would have its orbital speed `v` proportional to
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionThe gravitational potential energy of body of mass 'm' at the earth's surface -`mgR_(e)`. Its gravitational potential energy at a height `R_(e)` from the earth's surface will be (here `R_(e)` is the radius of the earth)
View SolutionIf `g` is same at a height `h` and at a depth `d`, then
View SolutionA solid sphere of radius `R//2` is cut out of a solid sphere of radius `R` such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was `M`. If a particle of mass `m` is placed at a distance `2.5R` from the centre of the cavity, then what is the gravitational attraction on the mass `m`?

View SolutionA geo-stationary stellite orbits around the earth in a circular orbit of radius 36,000km. Then, the time period of a spy stellite orbitting a few hundred km above the earth's surface `(R_(earth) = 6400km)` will approximately be
View SolutionIf `W_(1) W_(2)` and `W_(3)` represent the work done in moving a particle from `A` to `B` along three different paths `1.2` and`3` respectively (asshown ) in the gravitational fieled of a point mass m, find the correct relation between ` `W_(1) W_(2)` and `W_(3)`
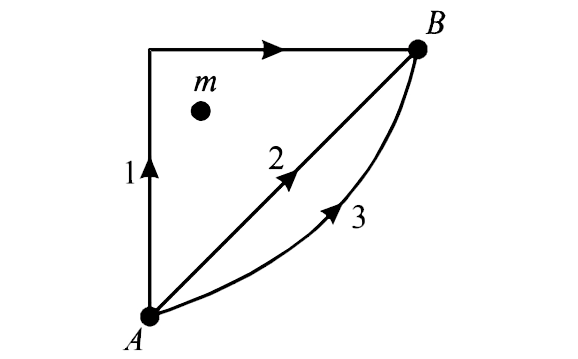
View SolutionIf `R` is the radius of the earth and `g` the acceleration due to gravity on the earth's surface, the mean density of the earth is
View SolutionA satellite moves around the earth in a circular orbit with speed `v`. If `m` is the mass of the satellite, its total energy is
View SolutionThe value of `g` (acceleration due to gravity) at earth's surface is `10 ms^(-2)`. Its value in `ms^(-2)` at the centre of the earth which is assumed to be a sphere of radius `R` metre and uniform mass density is
View SolutionTwo satellites `A` and `B` of masses `m_(1)` and `m_(2)(m_(1)=2m_(2))` are moving in circular orbits of radii `r_(1)` and `r_(2)(r_(1)=4r_(2))`, respectively, around the earth. If their periods are `T_(A)` and `T_(B)`, then the ratio `T_(A)//T_(B)` is
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionIf the radius of the earth decreases by `10%`, the mass remaining unchanged, what will happen to the acceleration due to gravity?
View SolutionThe maximum vertical distance through which a fully dressed astronaut can jump on the earth is `0.5 m`. If mean density of the Moon is two-third that of the earth and radius is one quarter that of the earth, the maximum vertical distance through which he can jump on the Moon and the ratio of the time of duration of the jump on the Moon to hold on the earth are
View SolutionTwo equal masses each in are hung from a balance whose scale pans differ in vertical height by `h`. The error in weighing in terms of density of the earth `rho` is
View SolutionThe distances from the centre of the earth, where the weight of a body is zero and one-fourth that of the weight of the body on the surface of the earth are (assume `R` is the radius of the earth)
View SolutionIf a man at the equator would weigh `(3//5)`th of his weight, the angular speed of the earth is
View SolutionThe distance between the centres of the Moon and the earth is `D`. The mass of the earth is `81` times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionTwo bodies with masses `M_(1)` and `M_(2)` are initially at rest and a distance `R` apart. Then they move directly towards one another under the influence of their mutual gravitational attraction. What is the ratio of the distances travelled by `M_(1)` to the distance travelled by `M_(2)`?
View SolutionIf g is the acceleration due to gravity on the earth's surface, the gain in the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth, is
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to `R^(-5//2)`, then
(a) `T^(2)` is proportional to `R^(2)`
(b) `T^(2)` is proportional to `R^(7//2)`
(c) `T^(2)` is proportional to `R^(3//3)`
(d) `T^(2)` is proportional to `R^(3.75)`.
View SolutionThe masses and radii of the Earth and the Moon are `M_1, R_1 and M_2,R_2` respectively. Their centres are at a distance d apart. The minimum speed with which a particel of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
View SolutionA spaceship is launched into a circular orbit close to the earth's surface . What additional velocity has now to be imparted to the spaceship in the orbit to overcome the gravitational pull. Radius of earth `= 6400 km`, `g = 9.8m//s^(2)`.
View SolutionA skylab of mass `m` kg is first launched from the surface of the earth in a circular orbit of radius `2R` (from the centre of the earth) and then it is shifted from this circular orbit to another circular orbit of radius `3R`. The minimum energy required to place the lab in the first orbit and to shift the lab from first orbit to the second orbit are
View SolutionConsider two satellites `A` and `B` of equal mass, moving in the same circular orbit of radius `r` around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy `E_(A) + E_(B)` of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
View SolutionA spherical shell is cut into two pieces along a chord as shown in the figure. `P` is a point on the plane of the chord. The gravitational field at `P` due to the upper part is `I_(1)`, and that due to the lower part is `I_(2)`. What is the relation between them?

View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionA rocket is launched vertically from the surface of earth with an initial velocity `v`. How far above the surface of earth it will go? Neglect the air resistance.
View SolutionThe gravitational potential due to earth at infinite distance from it is zero. Let the gravitational potential at a point `P` be `-5 J kg^(-1)`. Suppose, we arbitrarily assume the gravitational potential at infinity to be `+10 J kg^(-1)`, then the gravitational potential at `P` will be
View SolutionA projectile is fired from the surface of earth of radius `R` with a velocity `k upsilon_(e)` (where `upsilon_(e)` is the escape velocity from surface of earth and `k lt 1)`. Neglecting air resistance, the maximum height of rise from centre of earth is
View SolutionHow many hours would make a day if the earth were rotating at such a high speed that the weight of a body on the equator were zero
View SolutionTwo bodies of masses `M_(1)` and `M_(2)`, are placed at a distance `R` apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionIn the solar system, the Sun is in the focus of the system for Sun-earth binding system. Then the binding energy for the system will be [given that radius of the earth's orbit round the Sun is `1.5 xx 10^(11) m` and mass of the earth `= 6 xx 10^(24) kg`]
View SolutionA body is released from a point of distance `R'` from the centre of earth. Its velocity at the time of striking the earth will be `(R’gtR_(e))`
View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force of attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be
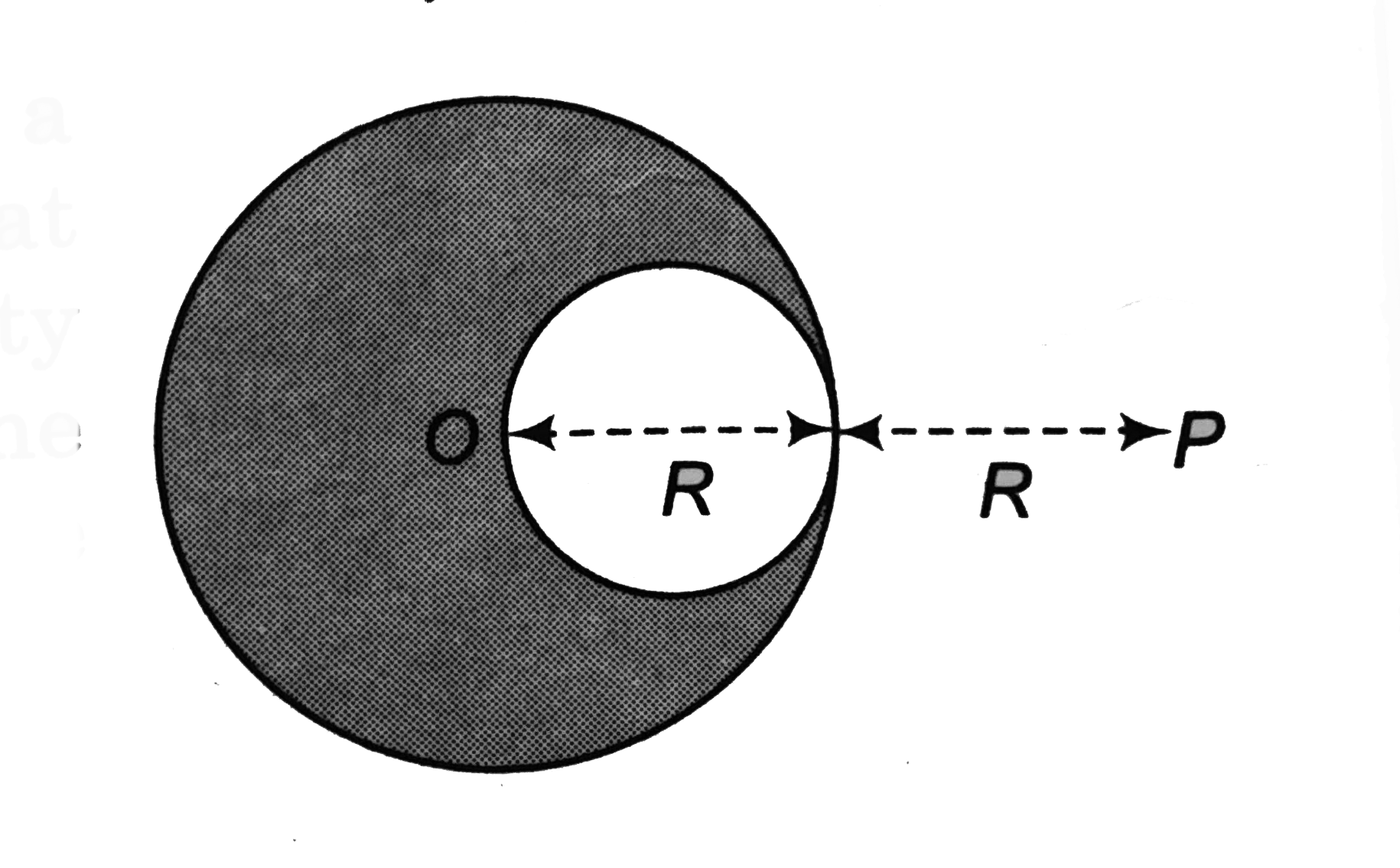
View SolutionThe value of `g` at a particular point is `10 m s^(-2)`. Suppose the earth shrinks uniformly to half of its present size without losing any mass. The value of `g` at the same point (assuming that the distance of the point from the centre of the earth does not change) will now be
View SolutionTwo satellites of masses of `m_(1)` and `m_(2)(m_(1)gtm_(2))` are revolving round the earth in circular orbits of radius `r_(1)` and `r_(2)(r_(1)gtr_(2))` respectively. Which of the following statements is true regarding their speeds `v_(1)` and `v_(2)`?
View SolutionThe earth moves around the Sun in an elliptical orbit as shown in Fig. The ratio `OA//OB=x`. The ratio of the speed of the earth at `B` to that at `A` is nearly
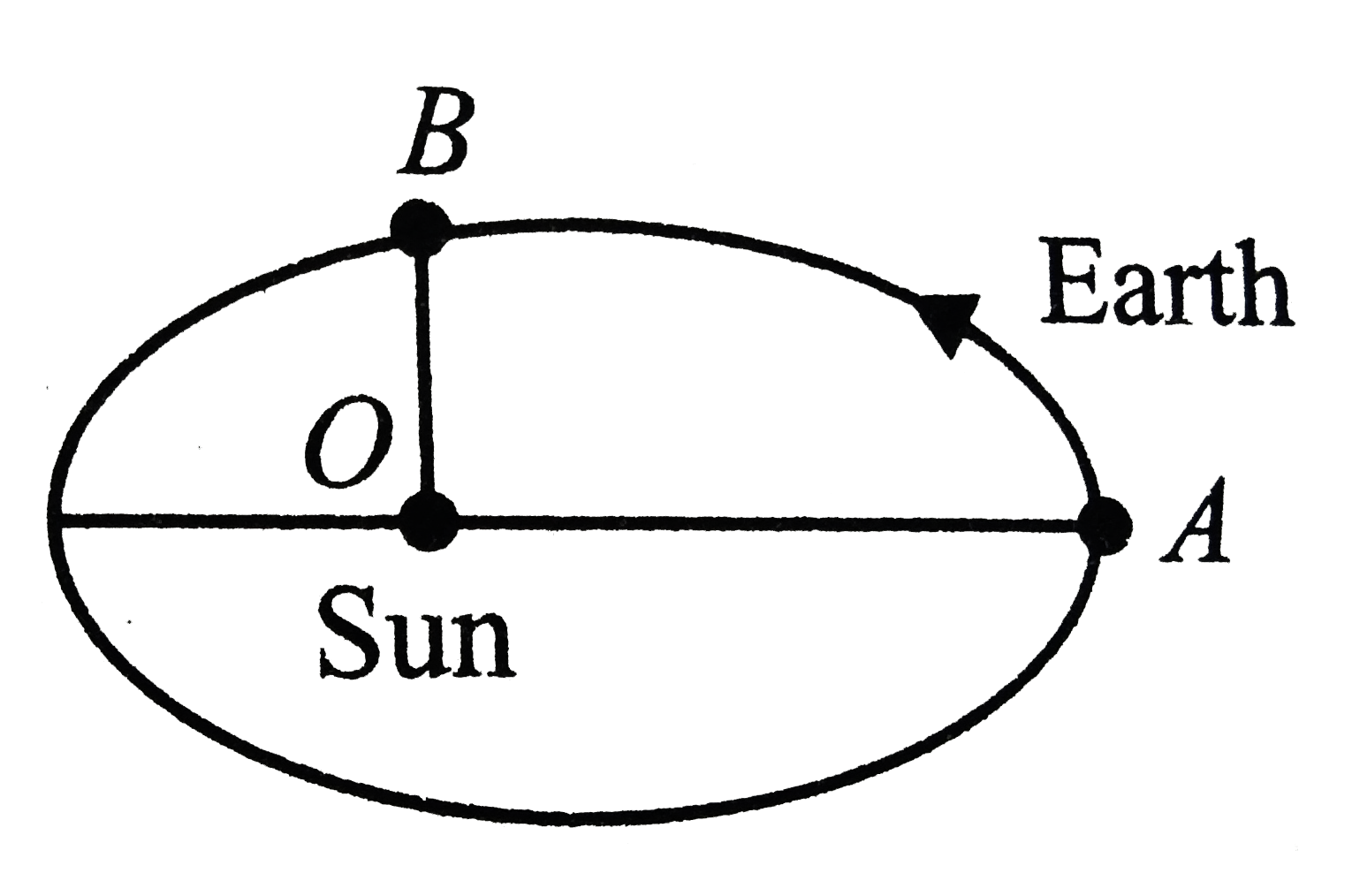
View SolutionFigure shows two shells of masses `m_(1)` and `m_(2)`. The shells are concentric. At which point, a particle of mass `m` shall experience zero force?
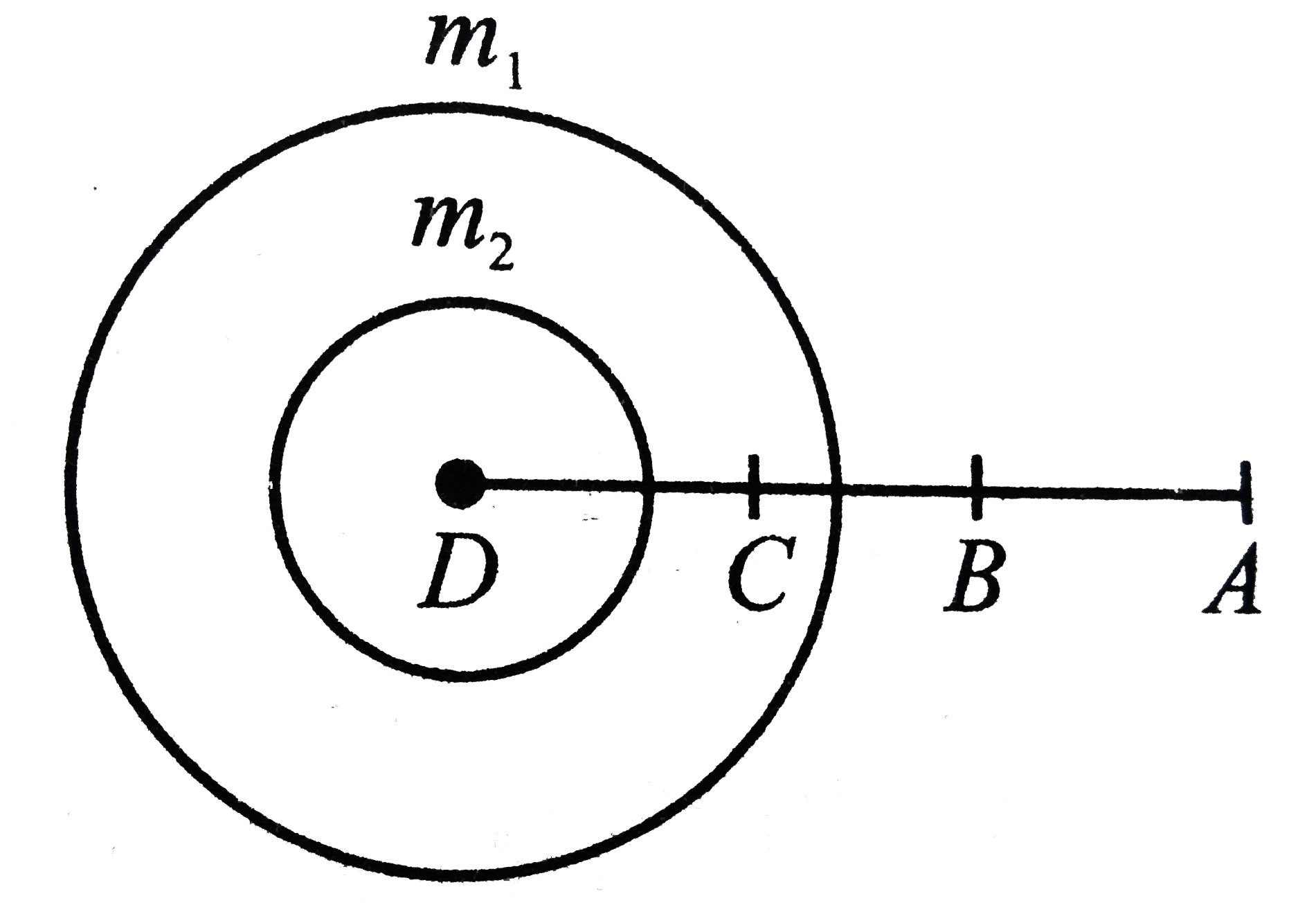
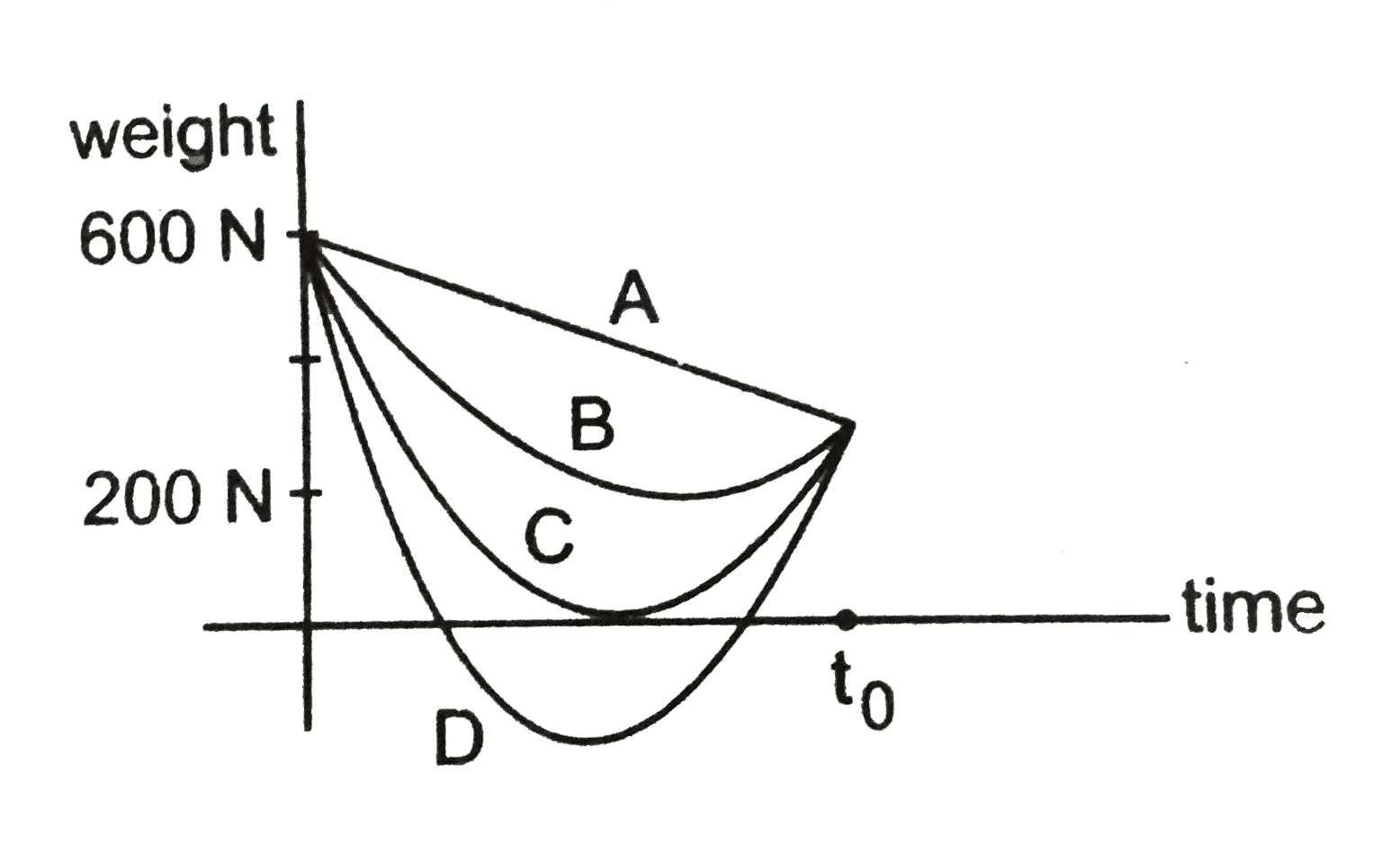
View SolutionSuppose the acceleration due to gravity at earth's surface is `10ms^-2` and at the surface of Mars it is `4.0ms^-2`. A passenger goes from the to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
View SolutionTwo satellites `A` and `B` of the same mass are revolving around the earth in the concentric circular orbits such that the distance of satellite `B` from the centre of the earth is thrice as compared to the distance of the satellite `A` from the centre of the earth. The ratio of the centripetal force acting on `B` as compared to that on `A` is
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionWhat is the mass of the planet that has a satellite whose time period is `T` and orbital radius is `r`?
View SolutionIf the mass of a planet is `10%` less than that of the earth and the radius is `20%` greater than that of the earth, the acceleration due to gravity on the planet will be
View SolutionIf a man at the equator would weigh `(3//5)`th of his weight, the angular speed of the earth is
View SolutionIn order to shift a body of mass `m` from a circular orbit of radius `3R` to a higher orbit of radius `5R` around the earth, the work done is
View SolutionA uniform ring of mas `m` and radius `a` is placed directly above a uniform sphere of mass `M` and of equal radius. The centre of the ring is at a distance `sqrt3a` from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionThe value of `g` at a certain height `h` above the free surface of the earth is `x//4` where `x` is the value of `g` at the surface of the earth. The height `h` is
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance `r_(1)` and farthest away at a distance of `r_(2)`. If `v_(1)` and `v_(2)` are the linear velocities at these points respectively, then the ratio `(v_(1))/(v_(2))` is
View SolutionMasses of `1 kg` each are placed `1 m, 2 m, 4 m, 8 m`, ... from a point `P`. The gravitational field intensity at `P` due to these masses is
View SolutionSuppose that the acceleration of a free fall at the surface of a distant planet was found to be equal to that at the surface of the earth. If the diameter of the planet were twice the diameter of the earth, then the ratio of mean density of the planet to that of the earth would be
View SolutionThree uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionA body of mass `m` rises to a height `h=R//5` from the earth's surface where `R` is earth's radius. If `g` is acceleration due to gravity at the earth's surface, the increase in potential energy is
View SolutionA man weighs `80 kg` on the surface of earth of radius `r`. At what height above the surface of earth his weight will be `40 kg`?
View SolutionThe gravitational potential energy of an isolated system of three particles, each of mass `m`, at the three corners of an equilateral triangle of side `l` is
View SolutionA diametrical tunnel is dug across the earth. A ball dropped into the tunnel from one side. The velocity of the ball when it reaches the centre of the earth is [Given: gravitational potential at the centre of earth `= -3//(2GM//R)`]
View SolutionConsider two solid uniform spherical objects of the same density `rho`. One has radius `R` and the other has radius `2R`. They are in outer space where the gravitational fields from other objects are negligible. If they are arranged with their surface touching, what is the contact force between the objects due to their traditional attraction?
View SolutionA body starts from rest from a point distant `r_(0)` from the centre of the earth. It reaches the surface of the earth whose radius is `R`. The velocity acquired by the body is
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionThe mass of the earth is `81` times the mass of the Moon and the distance between the earth and the Moon is `60` time the, radius of the earth. If `R` is the radius of the earth, then the distance between the Moon and the point on the in joining the Moon and the earth where the gravitational force becomes zero is
View SolutionThree equal masses m are placed at the three corners of an equilateral tringle of side a. find the force exerted by this system on another particle of mass m placed at a. the mid point of a side b. at the centre of the triangle.
View SolutionSuppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
View SolutionTwo astronauts have deserted their spaceship in a region of space far from the gravitational attraction of any other body. Each has a mass of `100 kg` and they are `100 m` apart. They are initially at rest relative to one another. How long will it be before the gravitational attraction brings them `1 cm` closer together?
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionA projectile is fired from the surface of earth of radius `R` with a velocity `k upsilon_(e)` (where `upsilon_(e)` is the escape velocity from surface of earth and `k lt 1)`. Neglecting air resistance, the maximum height of rise from centre of earth is
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.
View SolutionTwo concentric shells of masses `M_(1)` and `M_(2)` are having radii `r_(1)` and `r_(2)`. Which of the following is the correct expression for the gravitational field on a mass `m`?

View SolutionA satellite of mass `m` is orbiting around the earth at a height `h` above the surface of the earth. Mass of the earth is `M` and its radius is `R`. The angular momentum of the satellite is independent of
View SolutionTwo concentric shells have masses `M` and `m` and their radii are `R` and `r`, respectively, where `R gt r`. What is the gravitational potential at their common centre?
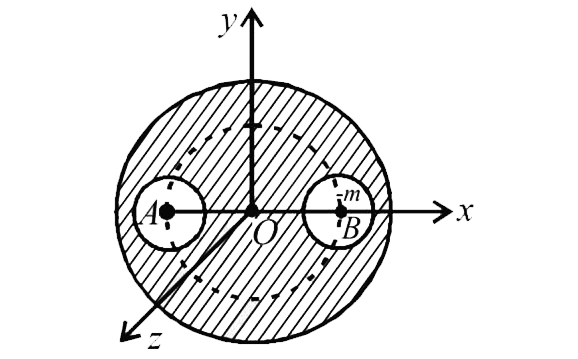
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionThree equal masses m are placed at the three corners of an equilateral tringle of side a. find the force exerted by this system on another particle of mass m placed at a. the mid point of a side b. at the centre of the triangle.
View SolutionFigure shows a planet in an elliptical orbit around the Sun `S`. Where is the kinetic energy of the planet maximum?

View SolutionThe escape velocity corresponding to a planet of mass `M` and radius `R` is `50 km s^(-1)`. If the planet's mass and radius were `4M` and `R`, respectively, then the corresponding escape velocity would be
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is `r` and farthest distance is `R`. If the orbital velocity of the planet closest to the Sun is `v`, then what is the velocity at the farthest point?
View SolutionThe radii of two planets are respectively `R_(1) and R_(2)` and their densities are respectively `rho_(1) and rho_(2)`.The ratio of the accelerations due to gravity at their surface is
View SolutionFigure shows the motion of a planet around the Sun `S` in an elliptical orbit with the Sun at the focus. The shaded areas `A` and `B` are also shown in the figure which can be assumed to be equal. If `t_(1)` and `t_(2)` represent the time taken for the planet to move from `a` to `b` and `c` to `d`, respectively then

View SolutionA body is fired with a velocity of magnitude `sqrt(gR)ltVltsqrt(2gR)` at an angle of `30^@` with the radius vector of the earth. If at the highest point, the speed of the body is `V//4`, the maximum height attained by the body is equal to
View SolutionA system of binary stars of mass `m_(A)` and `m_(B)` are moving in circular orbits of radii `r_(A)` and `r_(B)` respectively. If `T_(A)` and `T_(B)` are at the time periods of masses `m_(A)` and `m_(B)` respectively then
View SolutionTwo spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionThe change in the value of 'g' at a height 'h' above the surface of the earth is the same as at a depth 'd' below the surface of earth. When both 'd' and 'h' are much smaller then the radius of earth, then which one of the following is correct?
View SolutionA particle of mass 10g is kept on the surface of a uniform sphere of masss 100kg and radius 10cm. Find the work to be done against the gravitational force between them to take the particel far away from the sphere (you may take `G = 6.67xx10^(-11) Nm^2 /kg^2)`
View SolutionA tunnel is dug along the diameter of the earth. There is particle of mass `m` at the centre of the tunnel. Find the minimum velocity given to the particle so that is just reaches to the surface of the earth. `(R =` radius of earth)
View SolutionA cavity of radius `R//2` is made inside a solid sphere of radius `R`. The centre of the cavity is located at a distance `R//2` from the centre of the sphere. The gravitational force on a particle of a mass `'m'` at a distance `R//2` from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here `g=GM//R^(2)`, where `M` is the mass of the solid sphere]
View SolutionA satellite is seen after every `8` hours over the equator at a place on the earth when its sense of rotation is opposite to the earth. The time interval after which it can be seen at the same place when the sense of rotation of earth and satellite is same will be:
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionThe gravitational potential of two homogenous spherical shells `A` and `B` of same surface density at their respective centres are in the ratio `3:4`. If the two shells coalesce into a single one such that surface charge density remains the same, then the ratio of potential at an internal point of the new shell to shell `A` is equal to
View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `a`, at a distance `a` from its centre `C`. A small particle starts from `P` and reaches `C` under gravitational attraction only. Its speed at `C` will be.
View SolutionThe percentage change in the acceleration of the earth towards the Sun from a total eclipse of the Sun to the point where the Moon is on a side of earth directly opposite to the Sun is
View SolutionA comet is in highly elliptical orbit around the Sun. The period of the comet's orbit is `90` days. Some statements are given regarding the collision between the comet and the earth. Mark the correct statement. [Mass of the Sun `= 2 xx 10^(30) kg`, mean distance between the earth and the Sun `= 1.5 xx 10^(11)m`.]
View Solution
Single Correct questions and complete solutions for chapter GRAVITATION of CENGAGE PHYSICS (HINGLISH) of Class 11