Complete Solutions to Example of chapter CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| CP SINGH | Example |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
A pariticle is moving in a circle of radius `12m`. At an instant its speed is `6m//s` and the speed is increasing at the rate `4m//s^(2)`. Find the acceleration of the particle.
View SolutionA particle is moving in a circle of radius `R` and its speed is given by `v=lambdat^(2)`, where `lambda` is a constant. Find (a) radial acceleration, (b) tangential acceleration, ( c) resultant acceleration and (d) angle between acceleration and velocity.
View SolutionA point moves along an arc of a circle of radius `R`. Its velocity depends on the distance `s` covered as `v=lambdasqrt(s)`, where `lambda` is a constant. Find the angle `theta` between the acceleration and velocity as a function of `s`.
View SolutionA point moves along a circle with a velocity `v=t//2`. Find the acceleration of the point at the moment when it has covered a quarter circle from the beginning of motion.
View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations
are equal in moduli. At the initial moment `t=0` the velocity of the point equals `v_0`. Find:
(a) the velocity of the point as a function of time and as a function of the distance covered `s_1`,
(b) the total acceleration of the point as a function of velocity and the distance covered.
View SolutionThe kinetic energy of a particle moving along a circle of radius `R` depends on the distance covered `s` as `K=lambdas^(2)`, where `lambda` is a constant. Find the force acting on the particle as a function of `s`.
View SolutionA paricle of mass m moves along a circle of radius R with a normal acceleration varying with time as `w_n=at^2`, where a is a constant. Find the time dependence of the power developed by all the forces acting on the particle, and the mean value of this power averaged over the first t seconds after the beginning of motion.
View SolutionA balloon starts rising from the surface of the earth with a verticle component of velocity `v_(0)`. The baloon gathes a horizontal velocity `v_(x)=lambda_(y)`, where `lambda` is a constant and `y` is the height from the surface of earth, due to a horizontaln wind. determine (a) the equation of trajectory and (b) the tangential, normal and total acceleration of the balloon as a function of `y`.
View SolutionA particle moves in a circle of radius `4m` with a linear speed of `20m//s`. Find the angular speed.
View SolutionA ball is moving in a circle of radius `3m`. At a certain instant its angular speed is `2rad//s` and the angular speed is increasing at `3rad//s^(2)`. Find the tangential and centripetal components of the acceleration of the ball and magnitude of acceleration.
View SolutionFind the acceleration of a particle placed on the surface of the earth at the equator due to earth's rotation. The diameter of erth =12800 km andit takes 24 hour for the earth to comlete one revolution about its axis.
View SolutionSpotlight `S` rotates in a horizontal plane with constant angular velocity of `0.1 ` radian //second`. The spot of light `p` moves along the wall at a distance of `3 m ` . The velocity of the spot `p` when `theta = 45(@)` (see - fig. ) is ……….. ` m//s `
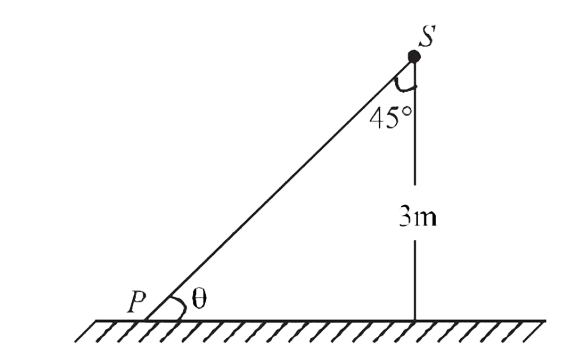
View Solution(a) Find the maximum speed at which a vehicle can turn round a curve of `20m` radius on a level road, `mu_(s)=0.5`.
(b) A circular track of radius `100 m` is to be designed for vehicles at an average speed of `72km//h`. Find the angle of banking of the track.
View SolutionA train has to negotitate a curve of radius `2000m`. By how much should the outer rail be raised with respect to inner rail for a speed`72 km//h`. The distance between the rails is `1m`.
View SolutionA body of mass `200g` tied to one end of string is revolved in a horizontal circle of radius `50cm` with angular speed `60` revolution per minute `("rpm")` on a smooth horizontal surface. Find (a) linear speed, (b) the acceleration and ( c) tension in the sting. what will happen if string is broken? (Take `pi^(2)=10)`
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Sch a system is called a conical pendulum.
View SolutionA string of length `50cm` is fixed at one end and carries a mass of `200g` at the other end. The string makes `5//2pi` revolution per second around the verticle axis through the fixed end. Calculate (a) the tension in the string (b) the angle of incilination of the string with verticle and (c) linear velocity of the mass.
View SolutionA coical pendulum consists of a string of length `L` whose upper end is fixed and another end is tied to a bob. The bob is moving in horizontal circle with constant angular speed `omega` such that the string makes a constant angle `theta` with the verticle. calculate time period `T_(0)` of revolution of bob in terms of `L,g` and `theta`.
View SolutionA large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and `theta` is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

View SolutionA particle of mass `m` is attacted to one end of string of length `3L`. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other end is attached to a small particle of mass `m_(0)`. The particle describe horizontal circular motion with angular velocity `omega_(1)` and `omega_(2)`. find the value of (a) `(omega_(1))/(omega_(2))` and (b) the value of `((1)/(omega_(1)^(2))+(1)/(omega_(2)^(2)))`.
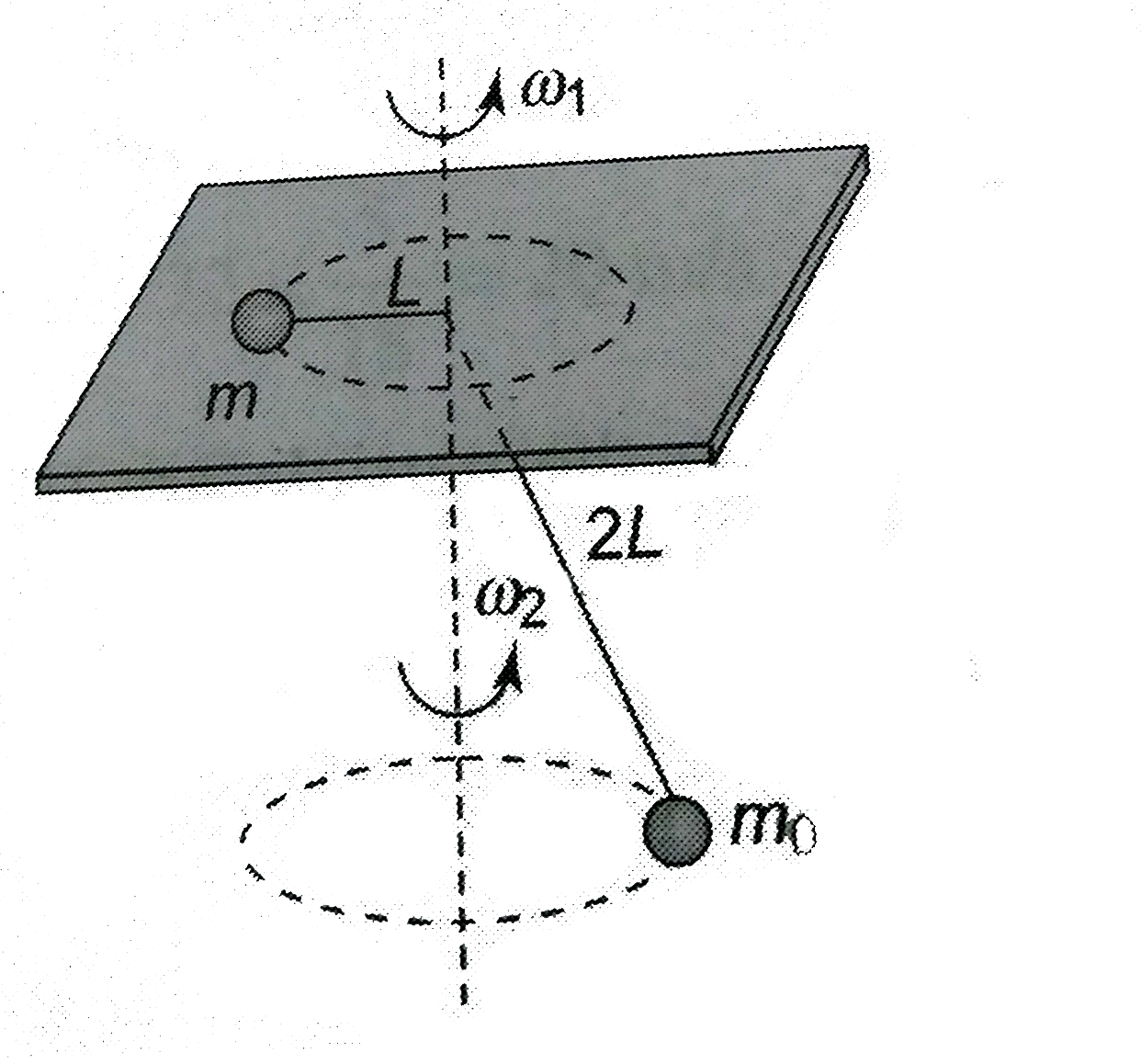
View Solutiona ball of mass `240g` is attached to the verticle rod by means of two strings. When the ball rotates about the axis of rod, the strings are extended as shown in the figure.
(a) find the angular speed of the ball if tension in lower string is `16N`.
(b) What is tension in the upper string?

View SolutionConsider the situation as shown in the figure. A rod of length `L=2//27m` pivodated near an end which is made to rotate in a horizontal plane with a constant angular speed. A ball is suspended bu a string also of length `2//27m` from the other end of the rod. if the string makes `theta=53^(@)` with vertical, find the angular speed of rotation.

View SolutionA particle describes a horizontal circle on smooth inner surface of a conical funnel as shown. If the height of the plane of the circle. Above the vertax is `10cm`, find the speed of the paricle.
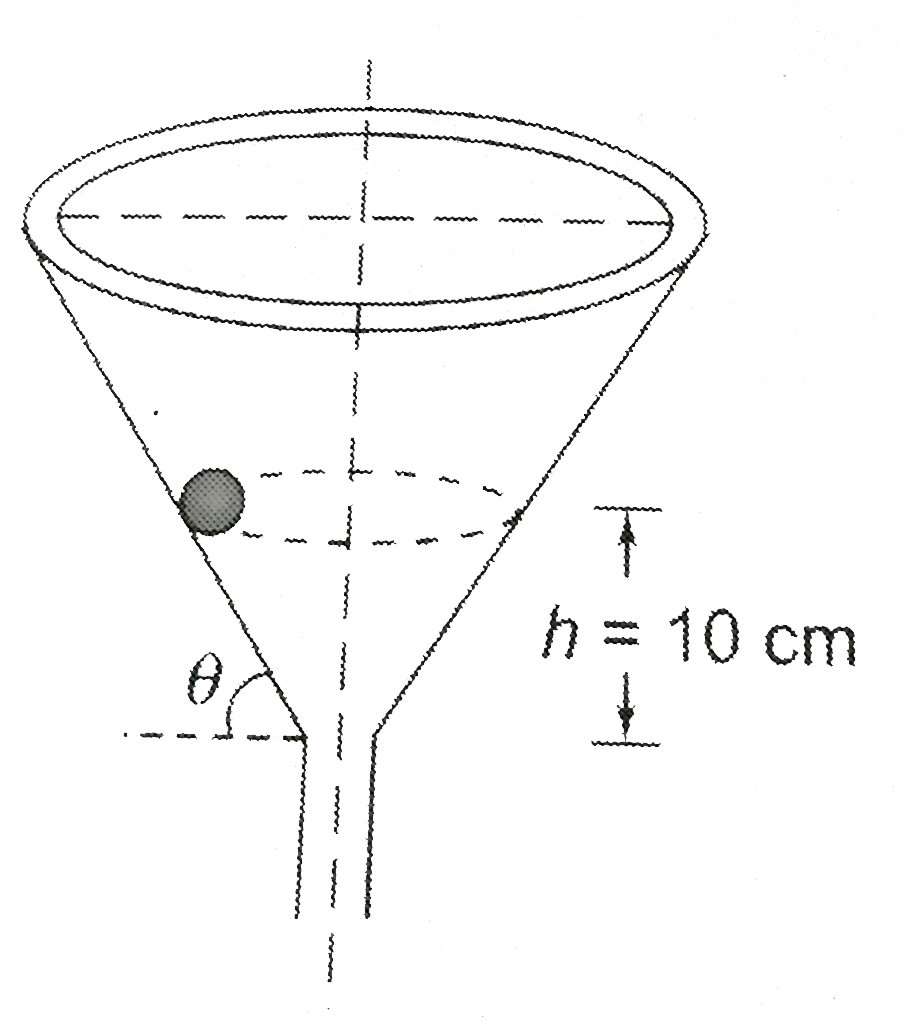
View SolutionA hemispherical bowl of radius `R=0.1m` is rotating about its own axis (which is verticle) with an angular velocity `omega`. A particle of mass `10^(-2)kg` on the smooth inner surface of the bowl is also rotating with the same `omega`. The particle is at a height `h` from the bottom of the bowl (a) obtain the relation betweemn `h` and `omega`. what is the minimum value of `omega` needed, in order to have a non-zero value of `h`? (b) it is desired to measure `g` using this set up, by measuring `h` accurately. assuming that `R` and `Omega` are known precisely and least count in the measurement of `h` is `10^(-4)m`, what is the minimum possible error `Deltag` in the measured value of `g`? `(g=10m//s^(2))`
View SolutionA small block of mass `m` moving on inside of the smooth hemisphere of radius `R`, describes a horizontal circle at a distance `R//2` below the centre of the sphere. Find the time period of revolution and force with which the block pushes against the hemisphere.
View SolutionOne end of a light spring constant `k` and natural length `l_(0)` is fixed and the other end is attached to a block of mass `m` lying on smooth horizontal surface. If the block is rotating in the horizontal circle of radius `l`, find the frequency of the revolution.
View SolutionTwo blocks of mass `m_(1)=10kg` and `m_(2)=5kg` connected to each other by a massless inextensible string of length `0.3m` are placed along a diameter of the turntable. The coefficient of friction between the table and `m_(1)` is `0.5` while there is no friction between `m_(2)` and the table. the table is rotating with an angular velocity of `10rad//s`. about a vertical axis passing through its center `O`. the masses are placed along the diameter of the table on either side of the center `O` such that the mass `m_(1)` is at a distance of `0.124m` from `O`. the masses are observed to be at a rest with respect to an observed on the tuntable `(g=9.8m//s^(2))`.
(a) Calculate the friction on `m_(1)`
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on `m_(1)`.
View SolutionA hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle `theta` with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is `mu`. Find the range of the angular speed for which the block will not slip.
View SolutionA car goes on a horizontal circular road of radius R, the speed increasing at a constant rate `(dv)/(dt)=a`. The friction coefficient between the road and the tyre is `mu`. Find the speed at which the car will skid.
View SolutionA body Is placed on a turntable. The friction coefficient between the body and the table is `mu`.
(a) If turntable rotates at constant angular speed `omega`, find the maximum value of `omega` for which the block will not slip.
(b) if the angular speed is increased uniformly from rest with an angular acceleration `alpha`, at what speed will the block slip?

View SolutionA block is rotating in contact with vertical wall (rotor) as shown. Find the minimum value of `omega` so that the block does not slide down.

View SolutionA cyclist rides along the circumference of a circular horizontal plane of radius `R`, with the friction coefficient `mu=mu_(0)(1-(r )/(R ))`, where `mu_(0)` is constant and `r` is distance from centre of plane `O`. Find the radius of the circle along which the cyclist can ride with the maximum velocity, what is this valocity?

View SolutionA ring of mass `m` and radius `R` is being rotated about its axis with constant angular velocity `omega` in the gravity free space. Find tension in the ring.
View SolutionWater of density `p` flows with a linear speed `v` through a horizontal rubber tube having the form of a ring of radius `R`. If the diameter of the tube is `d(ltlt R)`, find the tension in the rubber tube.
View SolutionA block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room onwhich the block moves is smoth but the friction coefficient between the wall and the block is `mu`. The block is given an initial speed `v_0`. As a function of the speed v write a. the normal force by the wall on the block. b. thefrictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration `((dv)/(dt)=v(dv)/(ds))` to obtain the speed of the block after one revoluton.
View SolutionA glass filled with water is whirled in a verticle circle of radius `R` what can be the minimum speed at the top of the path if water does not fall out from glass? If the glass moves with this speed, find the normal contact force the glass exerts on water at the lowest point of the path?
View SolutionAn aicraft loops the loop of radius `R=3000m` with a constant speed `v=200m//s`. Find the weight of the flyer of mass `m=60kg` in the lower, upper and middle points of the loop.
View SolutionThe middle point of a bridge, in the form of a circular arc on a canal of width `24m` at height `4m` from either end. Find the maximum speed at which a car can safely pass over the bridge.
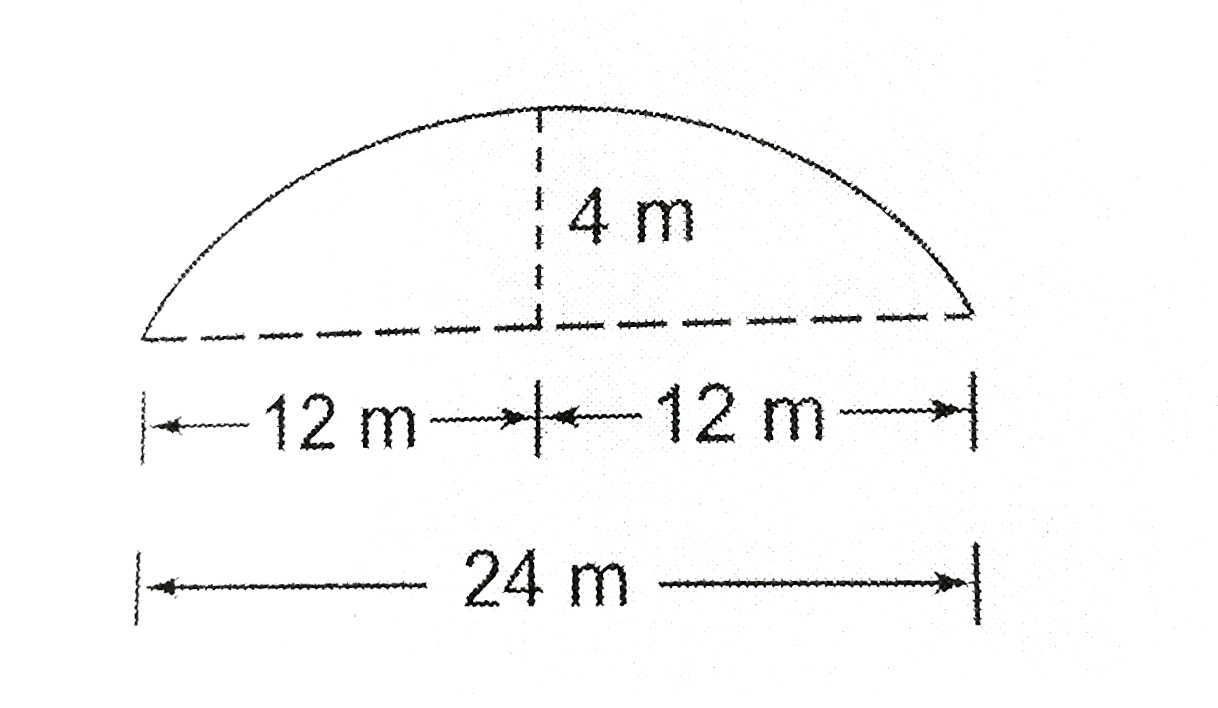
View SolutionA motorcycle has to move with a constant speed on an overbridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.
a. what can its maximum velocity be for which the contact with the road is not broken at the highest point?
b. If the motorcycle goes at speed `1/sqrt2` times the maximum found in part a. where will it lose the contact with the road?
c. What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
View SolutionThe bob of a pendulum at rest is given a sharp hit to impat a horizontal velocity `sqrt(10 gl)` where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of `60^0` with teh upward vertical.
View SolutionA ball of mass `m` is attached to a fixed point by a light inextensible string describe a circle in a verticle plane. The tension in the string has the values `alpha mg` and `beta mg`, respectively, when the particle is at the highest and the lowest point in the path. find the relation between `alpha` and `beta`.
View SolutionA stone of mass `m` tied to a light inextensible sting of length `L(=(10)/(3)m)` is whirling in a circular path of radius `L` in a verticle plane. If the ratio of the maximum to the minimum tension is four, find the speed of the stone at the highest point of the circle.
View SolutionConsider the situation as shown in the figure. The ball attached to a string is moving in the verticle circle find the (a) centripetal acceleration and (b) tanfential acceleration when the string makes an anhle `60^(@)` with lower vertical. Also, express the total acceleration in vector from taking `A` as origin.
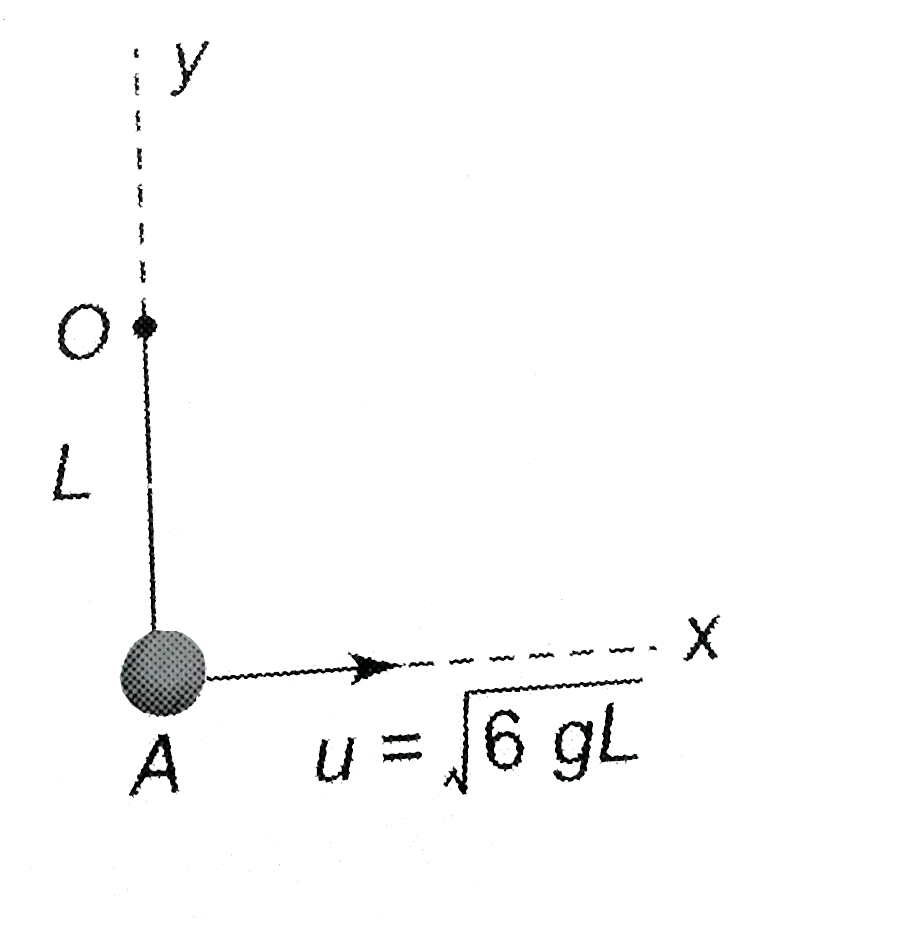
View SolutionA 40 kg mass, hanging at the end of a rope of length l, oscillates in a vertical plane with an angular amplitude `theta_0.` What is the tension in the rope when it makes en angle `theta` with the vertical ? If the breaking strength of the rope is 80 kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionA ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
View Solutiona small sphere of mass `m` susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of `theta`, the angle of deflection of the thread from the vertical. (b) Find the angle `theta` between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
View SolutionA simple pendulum consists of a ball of mass `m` connected to a string of length `L`. The ball is pulled aside so that the string makes an angle of `53^(@)` with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View SolutionConsider the situation as shown in the figure. Find `(T_(min))/(T_(max))`.
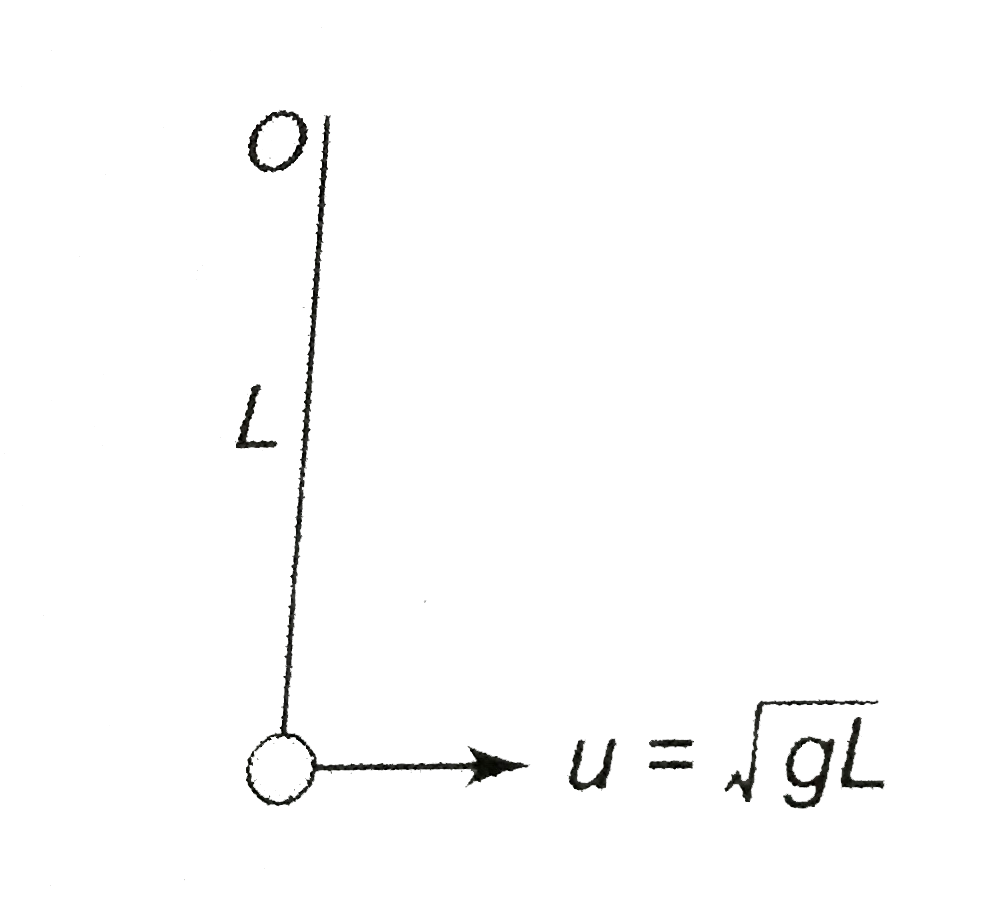
View SolutionThe bob of a simple pendulum is given a sharp hit impart it a horizontal speed of `sqrt(3gL)`. Find an angle made by the string with the upper verticle before it becomes slack. Also, calculate the maximum height attained by the bob above the point of suspension. `L` is length of the string.
View SolutionA simple pendulum of length `L` having a bob of mass `m` is first taken aside so that the string forms the tight angle with the verticle and then released. The string hits a peg which is fixed at a distance below the point of suspension and the bob starts going in a circle centered at the peg. find the minimum value of `y` for which the bob goes in a complete circle about the peg.

View SolutionA block is released from rest at the top of an inclined plane which later curves into a circular track of radius `r` as shown in figure. Find the minimum height `h` from where it should be released so that it is able to complete the circle.
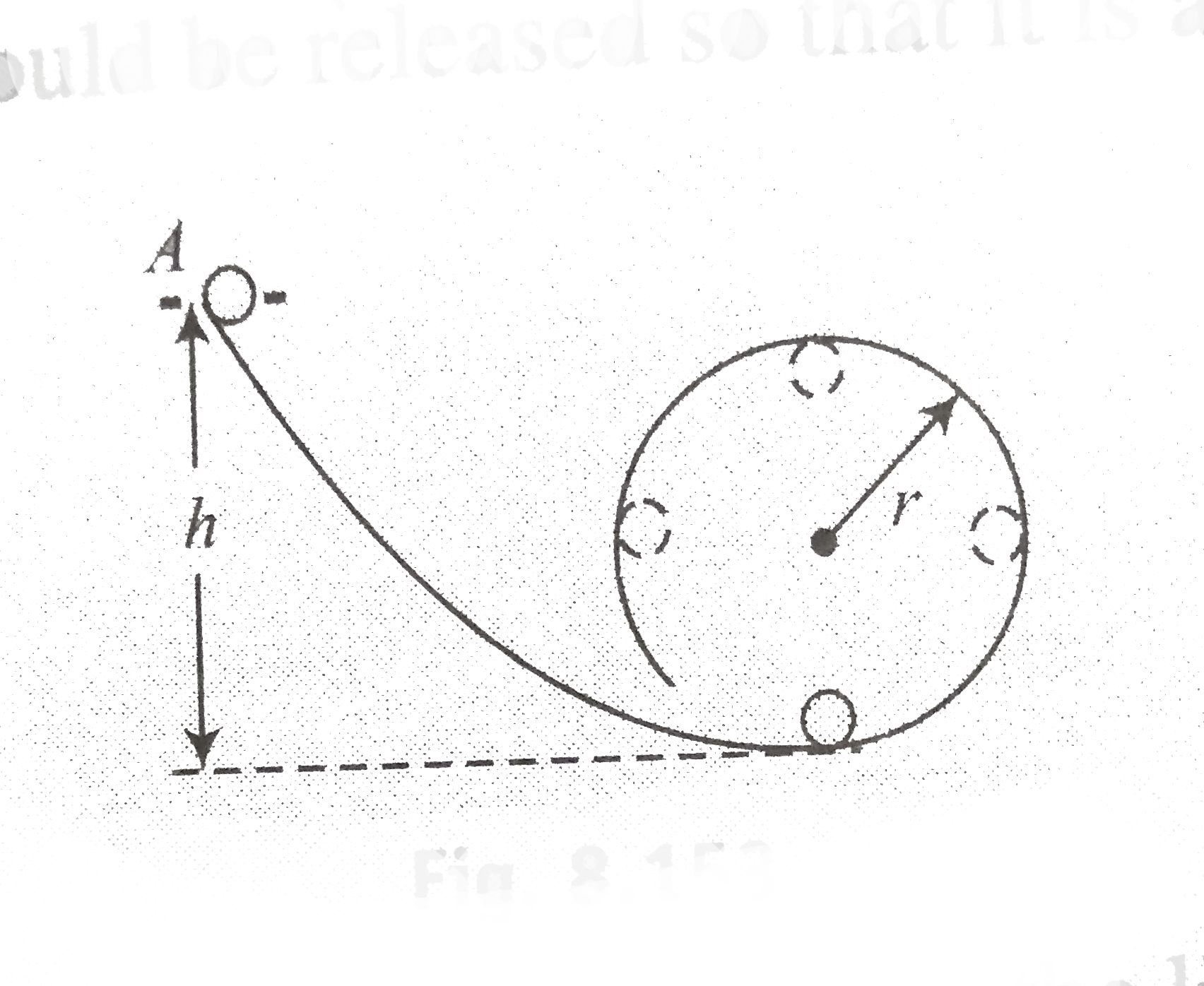
View SolutionA small body A starts sliding from the height h down an inclined groove passing into a half-circle of radius `h//2` (figure).

Assuming the friction to be negligible, find the velocity of the body at the highest point of its trajectory (after breaking off the groove).
View SolutionA small block of mass `m` slides along a smooth frictionless track as shown.
(a) If it starts from rest at `P`, what is the resultant force acting on it at `Q`?
(b) At what height above the bottom should the block be released so that the force it exerts against the track at the top of the loop equals its weight?

View SolutionA small object slides without friction from the height `5R//2` and then loops of the verticle loop of radius `R` from which a symmetrical section of angle `2alpha` has been removed. Find angle `alpha` such that after losing contact at `A` and flying through the air, the object will reach point `B`.

View SolutionA particle is released from the top of a smooth hemisphere.find the angle rotated by the radius through the particle, when it loses contract with the hemisphere. Also sketch variation of normal contact force with `cos theta`, where `theta` is an angle rotated by the radius through the particle.
View SolutionA particle of mass `m` is released from the top of a smooth hemisphere of radius `R` with the horizontal speed `mu`. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA particle of mass `m` is released on a fixed. Smooth sphere of radius `R` at a position, where the radius through the particle makes an angle of `alpha` with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? `(cos alpha=3//4)`
View SolutionA track consists of two circular parts `ABC` and `CDE` of equal radius `R` and joined smoothly as shown. Each part subtends an angle `2theta` at center. A vehicle of mass `m` travels with constant force by the road on the vehicle when it is at (i) `B` (ii) `D` (iii) just before `C` and (iv) just after `C`. (b) find the friction by the track on the vehicle when it is at `B`, `C` and `D`. (c) what should be the minimum friction coefficient between the road and the vehicle, which will ensure that cyclist can move with constant speed.

View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length `3R//4` is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of `60^@` with the vertical. The spring constant `K=mg//R`. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

View SolutionA small block of mass `m` is tied to the top of a smooth inclined plane with the help of a string of length `L` as shown in the figure. The inclined plane of inclination `theta` with horizontal is rotated with an angular velocity `omega` about a verticle axis passing through the end of the string fixed to the plane.
(a) Find the maximum value of `omega` so that the block maintains contact with the inclined plane.
(b) Find the ratio of the tension in the string and the normal reaction between the block and the plane.

View SolutionA table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius R Figure. A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on te tableare connected through a string going over the pulley. Initially the masses are held by a personwith the strings aslong teh outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the mases as seen from the cabin and the tension in the starting.
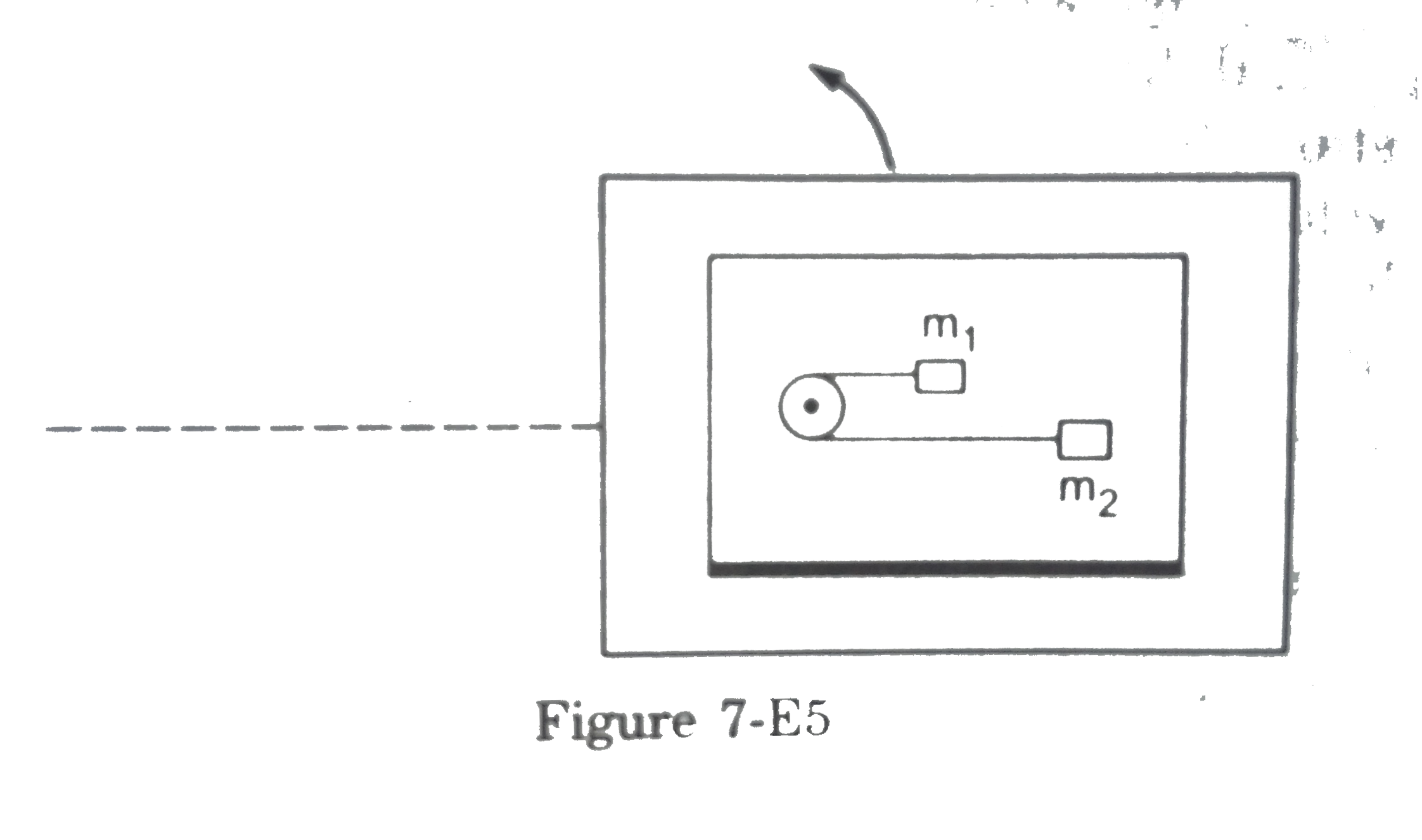
View SolutionA tube of length L is filled completely with an incomeressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity `omega.` The force exerted by the liquid at the other end is
View SolutionA rod of length L is pivoted at one end and is rotated with as uniform angular velocity in a horizontal plane. Let `T_1 and T_2` be the tensions at the points L//4 and 3L//4 away from the pivoted ends.
View SolutionA uniform chain of mass `m` and length `llt(piR)/(2)` is placed on a smooth hemisphere of radius `R` with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle `beta`.
View Solution
Example questions and complete solutions for chapter CIRCULAR MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11