Complete Solutions to EXAMPLES of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| CP SINGH | EXAMPLES |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
A force `vecF=10hati+2hatj+3hatk` N displaces a particle from `vecr_1=2hati+hatj+hatk` m to `vecr_2=4hati+2hatj+3hatk` m Find the work done by the force.
View Solution
For the surface `mu=0.4` find the work done by the applied force, friction and net force.
View SolutionA block of mass 5 kg is pulled along a horizontal. The friction coefficient between the block and the surface is `0.5`. If the block travels at constant velocity, find the work done by this applied force during a displacement 4 m of the block.
View SolutionA block of mass 2 kg is being brought down by a string. If the block acquires a speed `1(m)//(s)` in dropping down 25 cm, find the work done by the string in the process.
View SolutionThe two blocks in an Atwood machine have masses 2.0 kg and 3.0 kg. Find the work done by gravity during the fourth second after the system is released from rest.
View SolutionA force `F=2x+3x^2`N acts on a particle in the x-direction. Find the work done by this force during a displacement `x=1.0m ` to `x=2.0m`
View Solution
The variation of force acting on a particle along the x-axis is shown in the figure Find the work done by force during displacement `x=0` to `x=25cm`
View SolutionFind the work done if a particle is displaced from `J(1m,2m,3m)` to `K(2m,3m,4m)` under a force (a) `vecF=(2hati+5hatj+6hatk)N` and (b) `vecF=(2xhati+3y^2hatj+4z^3hatk)N`
View SolutionThe work done in extending a spring by `x_0` is `W_0`. Find the work done in further extension `x_0`.
View Solution
Consider the situation as shown in the figure. A constant horizontal force 45 N acting on the lower blocks produces an acceleration `4(m)//(s^2)`, the two blocks always move together. Find (a) coefficient of friction between the bigger block and the horizontal surface (b) friction acting on the upper block and (c ) work done by the friction on the upper block during a displacement 2m of the system.
View SolutionA block of mass `m` lying on a horizontal surface (coefficient of static friction `= mu_(s))` is to be brought into motion by a pulling force `F` At what angle `theta ` with the horizontal should the force `F` be applied so that its magnitude is minimum ? Also find the minimum magnitude

View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part n the table. The friction coefficient between the table and the chain is `mu`. Find the work done by the friction during the period the chain slips off the table.
View SolutionA particle of mass `m` moves on a straight line with its velocity varying with the distance traveled. Find the total work done by all the forces during a displacement `x=0` to `x=d` if the velocity is equal to (a) `v=lamdasqrtx` and (b) `v=lamdax` is constant.
View Solution
A ball of mass `200g` is attached to a string of length `50cm` and a force `F` is applied on it as shown. Find the work done by this force if string makes an angle `60^@` with vertical. In the initial and final position, speed of the ball is zero.
View SolutionA particle of mass 2 kg is moving in a straight line such that its velocity is given by `v=3t^2(m)//(s)`, where t is in second. Find the work done by all forces in the first 2 s of its motion.
View SolutionA small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of `theta`.
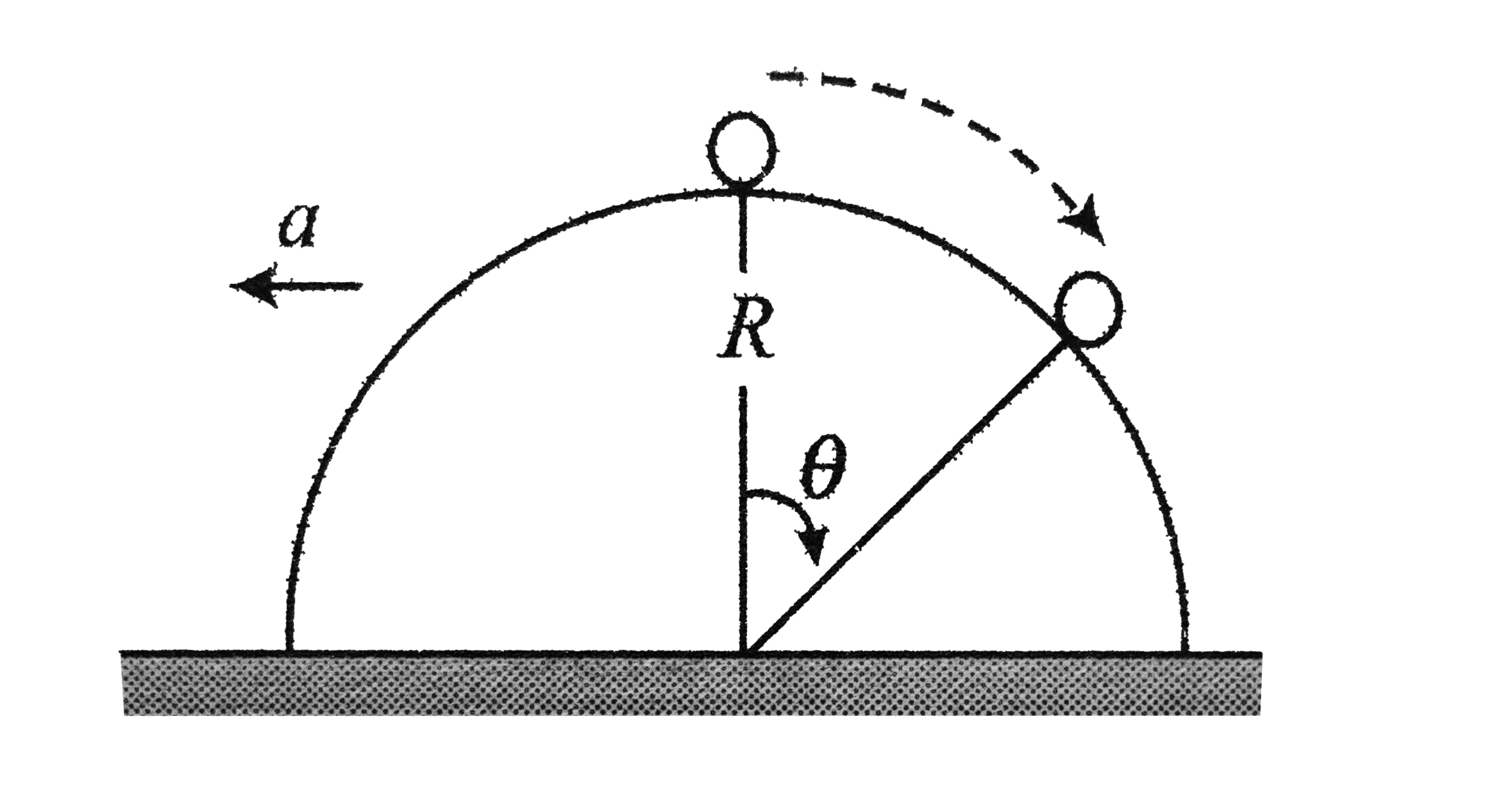
View SolutionA uniform chain of length `L` and mass `M` is tying on a smoth table and one third of its length is banging vertically down table the edge of the table if g is acceleration the to gravity , the work required to pull the hanging part on the table is
View SolutionTwo cyllindrical vessels of equal cross sectional ara A contain water upto heights `h_1` and `h_2`. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is `rho`
View Solution
A block is released from the top of the smooth inclined plane of height `h`. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA particle is thrown from the top of a tower of height `h` with speed `v_0` at an unknown angle. Find the speed with which it strikes the ground.
View Solution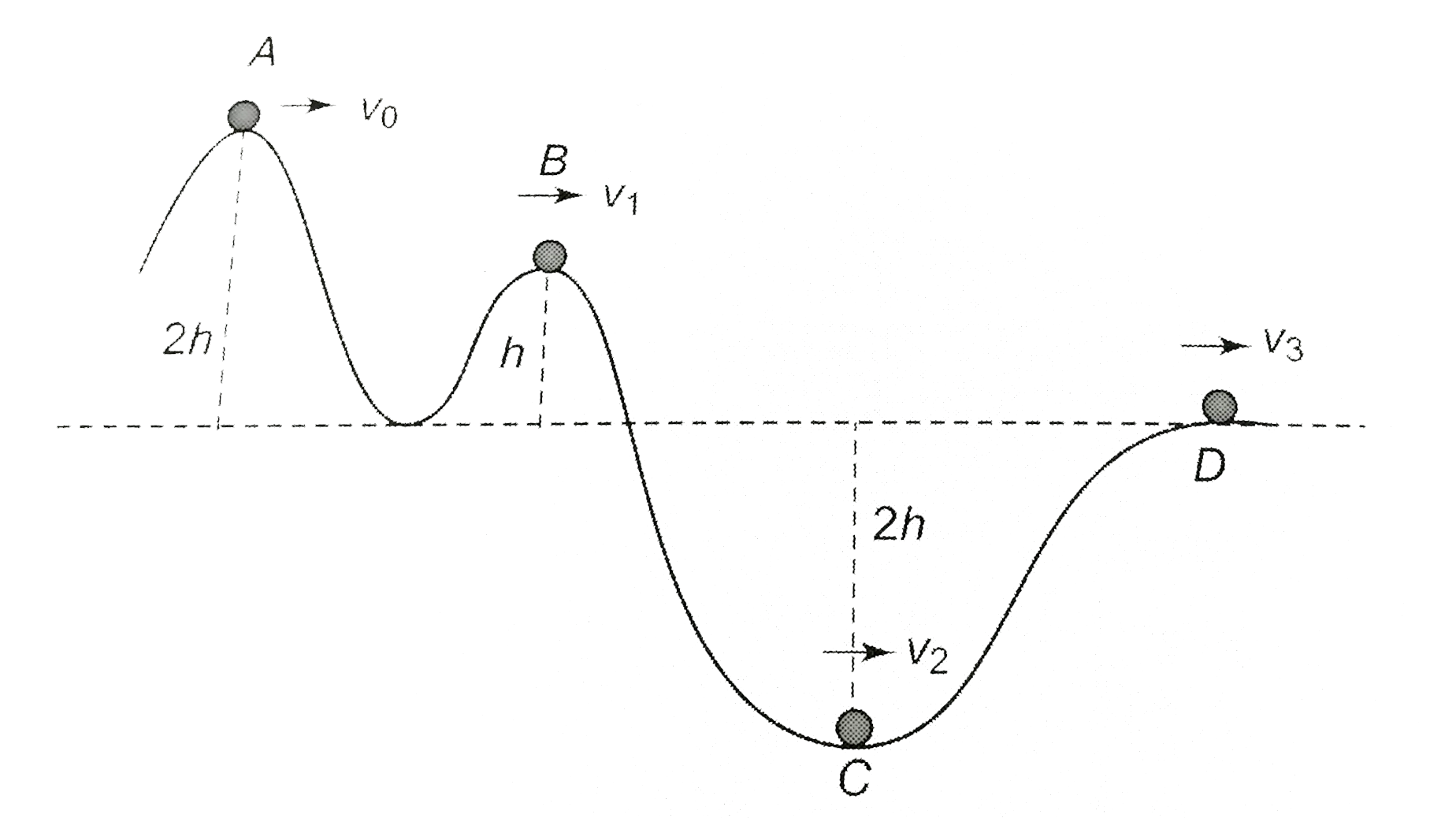
A particle is given velocity `v_0` at point A as shown in the figure. Find the speed of particle at point `B,C` and `D`
View Solution
A ball is attached to a string of length `L` and the ball is given velocity `v_0` at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.
View Solution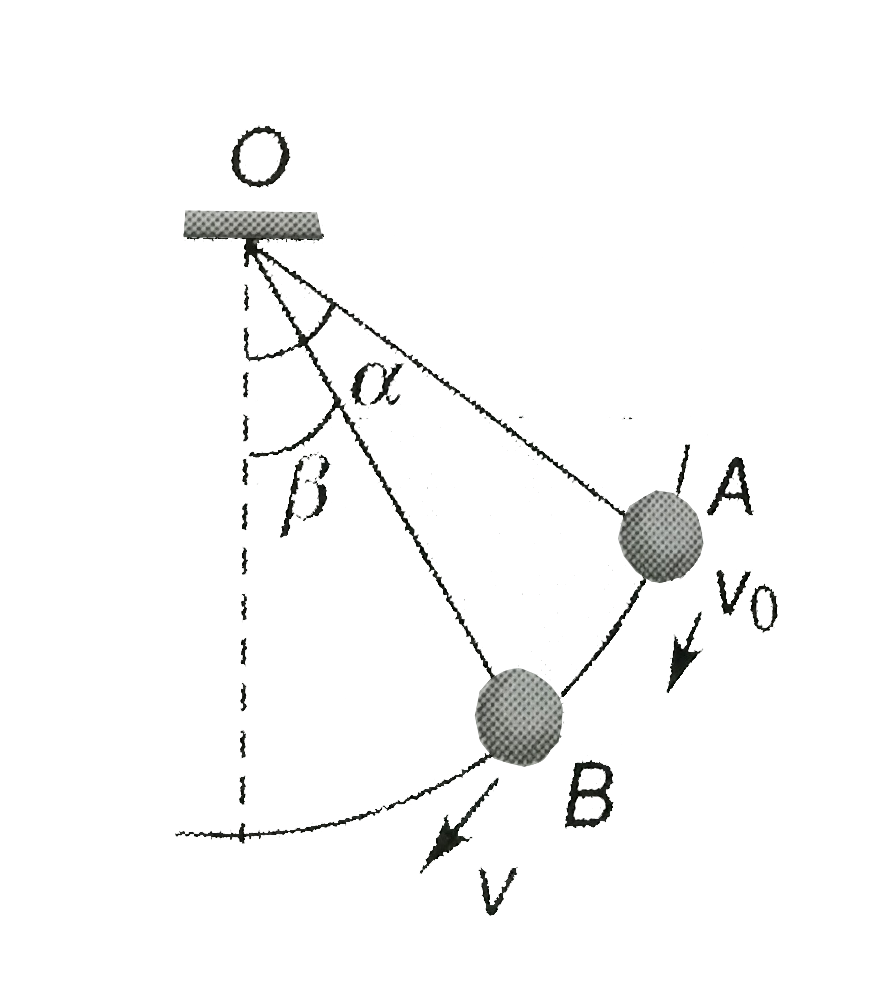
A ball attached to a string length `L` is oscillating line a simple pendulum. Find `v` in terms of `v_0` `L` `alpha` and `beta`.
View Solution
A block is released from position A in the following figure. Find the speed of the block in position B. Assume the surface as frictionless.
View Solution
Consider a uniform chain of mass `m` and length `L`, the chain is released when hanging length is `L_0`. Find the speed with which the chain leaves the table.
View SolutionA block of mass `m` moving at a speed `v_0` compresses a spring of spring constant `k` as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View Solution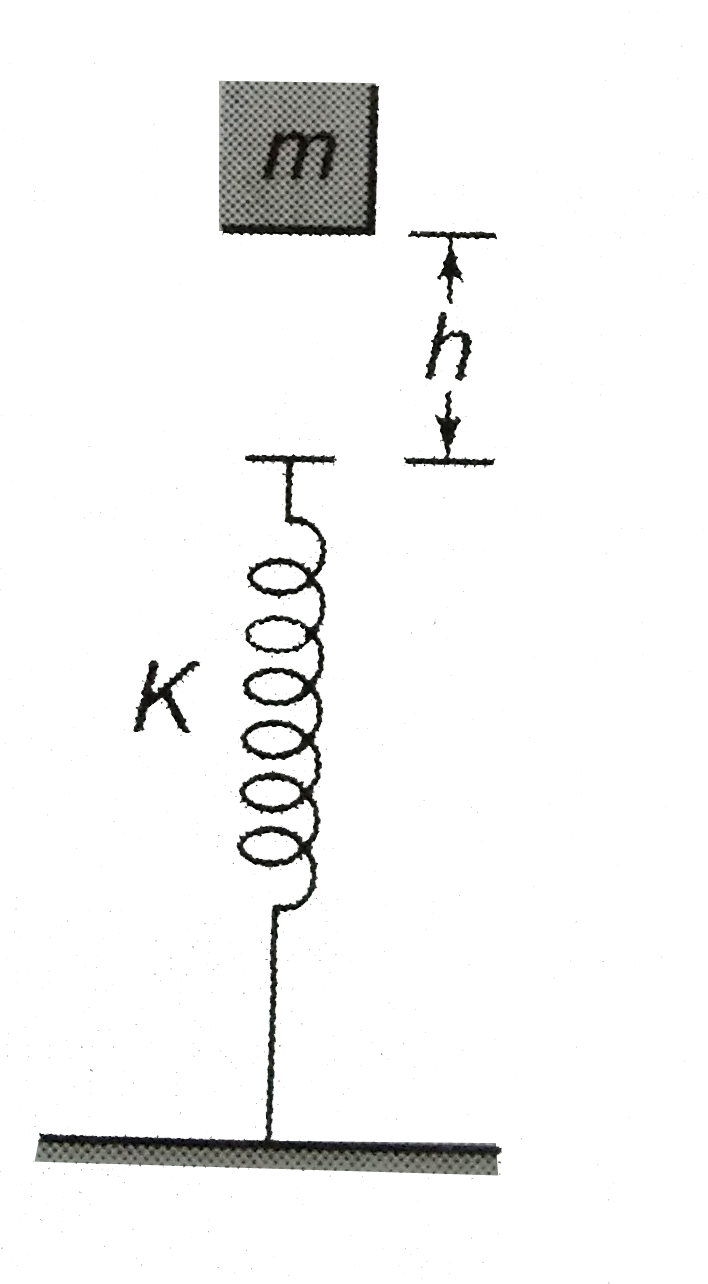
A block is released from height `h`, find the maximum compression of spring of spring constant `k`.
View Solution
A block of mass `m` is pressed against a horizontal spring fixed at one end to compress the spring through `(L_0)//(2)`. The natural length of the spring is `L_0` and spring constant `k=(mg)//(L_0)`. When released, the block moves horizontally on smooth surface till it leaves the spring. At what horizontal distance from O it strikes the ground.
View SolutionIn figure, the stiffness of the spring is `k` and mass of the block is `m`. The pulley is fixed. Initially, the block `m` is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block `m`. Neglect the mass of the spring and that of the string. Also neglect the friction.
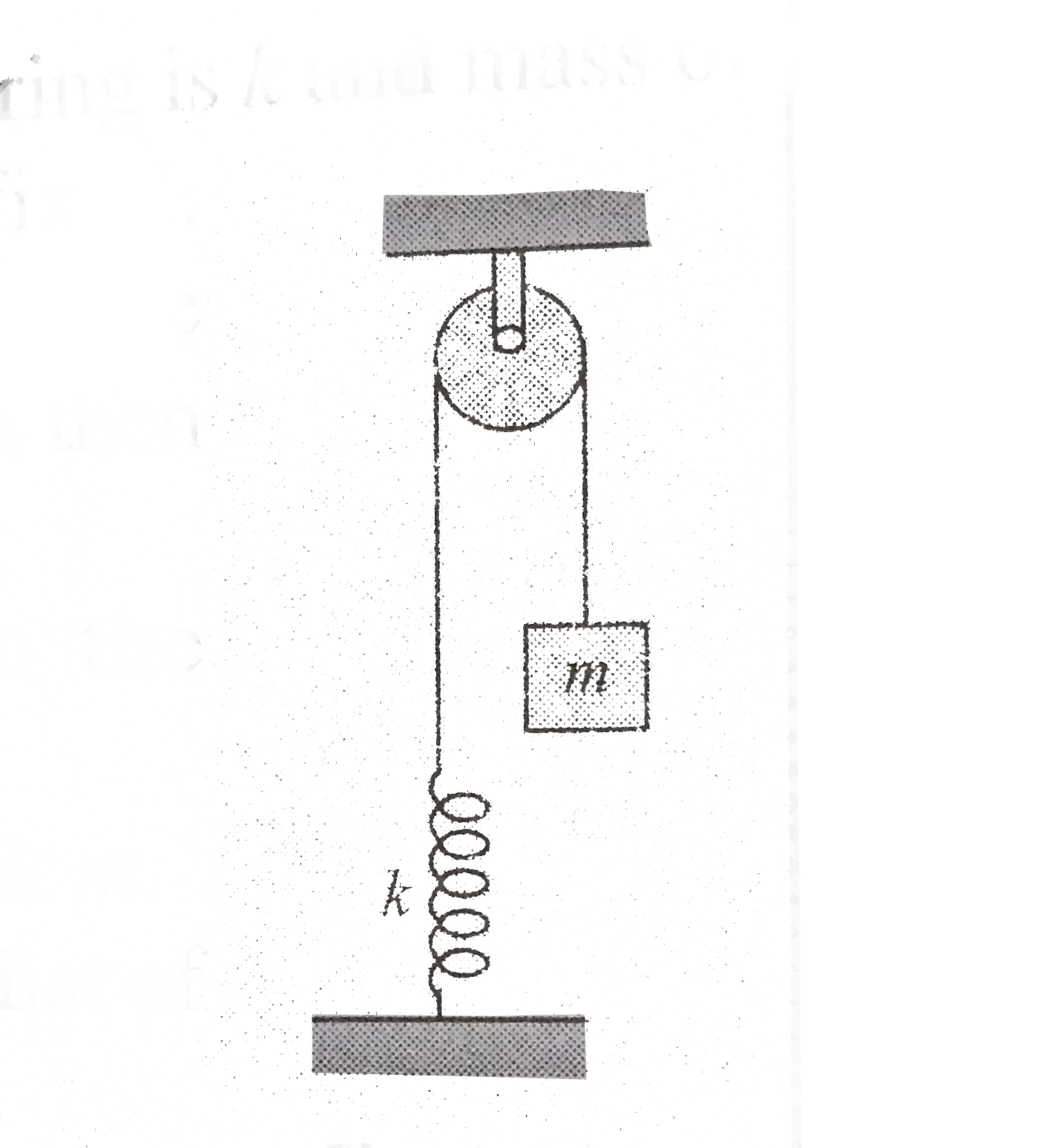
View SolutionA block of mass m is suspened through a spring of spring constant k and is in equlibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium psitin, the block comes to an instantaneous rest?
View Solution
A ring of mass `m` is attached to a horizontal spring of spring constant `k` and natural length `l_0`. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionIn the previous problem, the rod on which the ring slide is vertical Repeat the problem.
View SolutionA block of mass `m` is given velocity `v_0` on a rough horizontal surface. After traveling a distance d. Its speed becomes `(v_0)//(2)`. Find the work done against friction. The work donw by friction and the coefficient of friction.
View SolutionAn object of mass 4 kg falls from rest through a vertical distance of 20 m and reaches with velocity of 10 `(m)//(s)` on ground. How much work is done by air friction?
View SolutionA ball is thrown vertically upward with speed `10 m//s` and it returns to the ground with speed `8 m//s`. A constant air resistance acts. The minimum height attained by the ball is
View Solution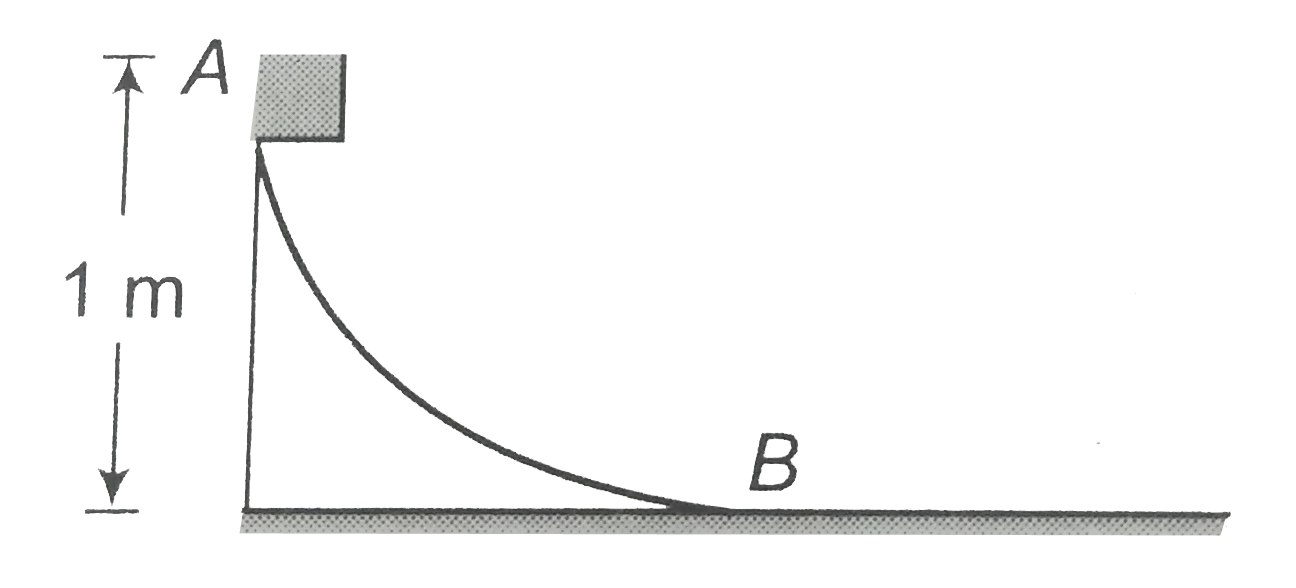
A block weighing 10 kg travels down a smooth curved track AB joined to a rough horizontal surface (see the figure.) The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1 m above the horizontal surface, how far will it move on the rough surface?
View Solution
The curved portions are smooth and horizontal surface is rough. The block is released from `P`. At what distance from A it will stop?the friction coefficient for rough flat surface is 0.2.
View SolutionA body of mass m is pushed with the initial velocity `v_0` up an inclined plane set at an angle `alpha` to the horizontal. The friction coefficient is equal to k. What distance will the body cover before it stops and what work do the friction forces perform over this distance?
View SolutionA disc of mass `m` slides with the zero initial velocity down an inclined plane of inclination `theta` to the harizontal, having traveled the distance `d` along the horizontal plane, the disc stops. Find the work performed by the friction over the whole distance, assuming the friction coefficient `mu` for both the inclined and horizontal planes.
View Solution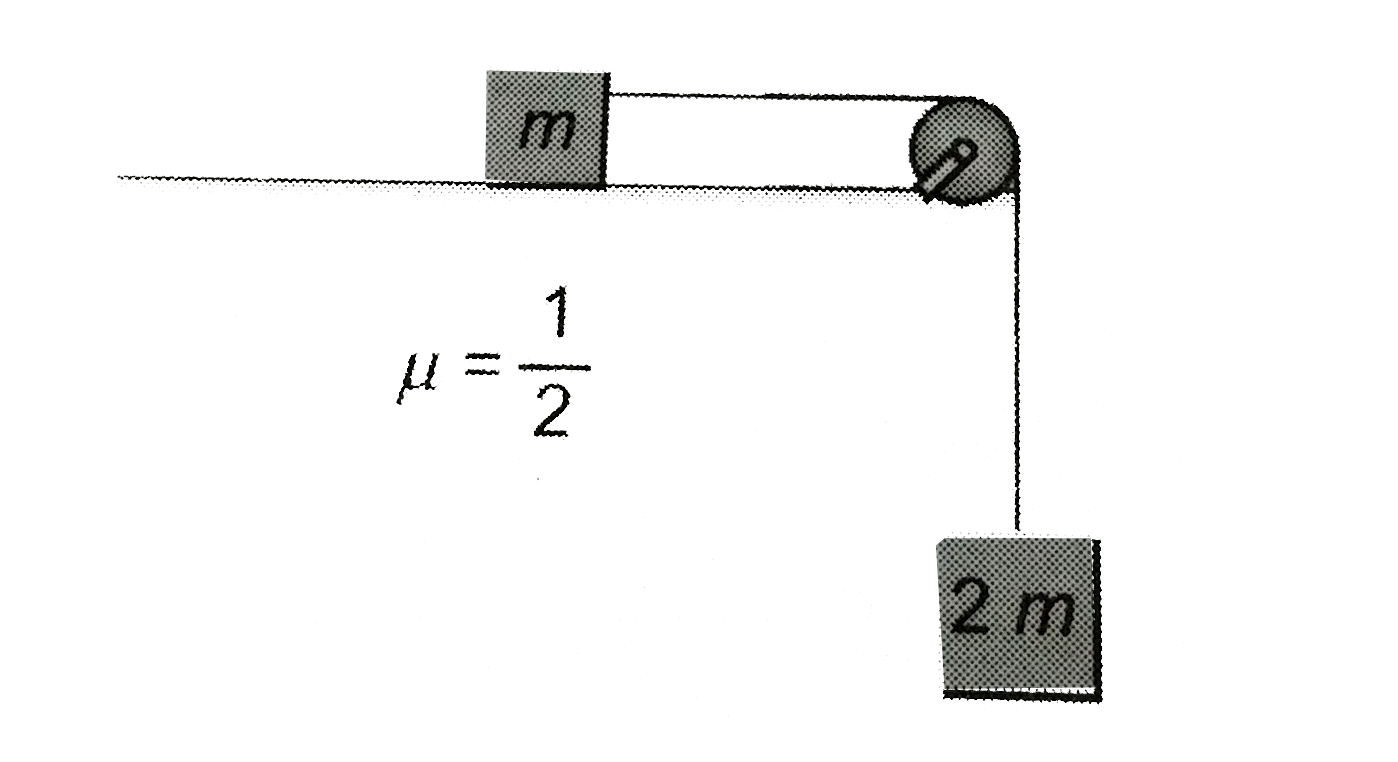
Consider the situation as shown in the figure. The system is released from rest. Find the speed of `m` when it has traveled a distance `d` on a rough surface.
View SolutionA ball of mass `m` is moved with speed `v_0` at the highest point in a closed circular tube of radius `R` kept in the vertical plane. The cross-section of the tube is such that the block just fits in it. The block makes several oscillations inside the tube and finally stops at the lowest point. Find the work done by the tube on the block during the process.
View Solution
Consider a situation as shown in the figure. The system is released from rest. When the block of mass `m` has falled a distance `L`, its speed becomes `(sqrt(gL))/(3)`. Find the friction coefficient `mu`.
View Solution
A block of mass 200 g is given velocity `2(m)//(s)` on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant `k=100(N)//(m)`
View SolutionA `0.5kg` block slides from the point A on a horizontal track with an initial speed `3 m//s` towards a weightless horizontal spring of length `1m` and force constant `2N//m.` The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and `0.20` respectively. If the distances AB and BD are `2m` and `2.14m` respectively, find total distance through which the block moves before it comes to rest completely. `(g=10 m//s^(2) ).
View SolutionA 20 kg body is released from rest so as to slide in between vertical rails and compresses a vertical spring `(k=1920(N)/(m)`) placed at a distance `h=1.0`m from the strating position of the body. The rails offer a frictional force of 40 N opposing the motion of body. Find (a) the velocity v of the body just before striking with the spring, (b) the maximum compression of the spring and (c ) the distance `h^(')` through which the body is rebounded up.
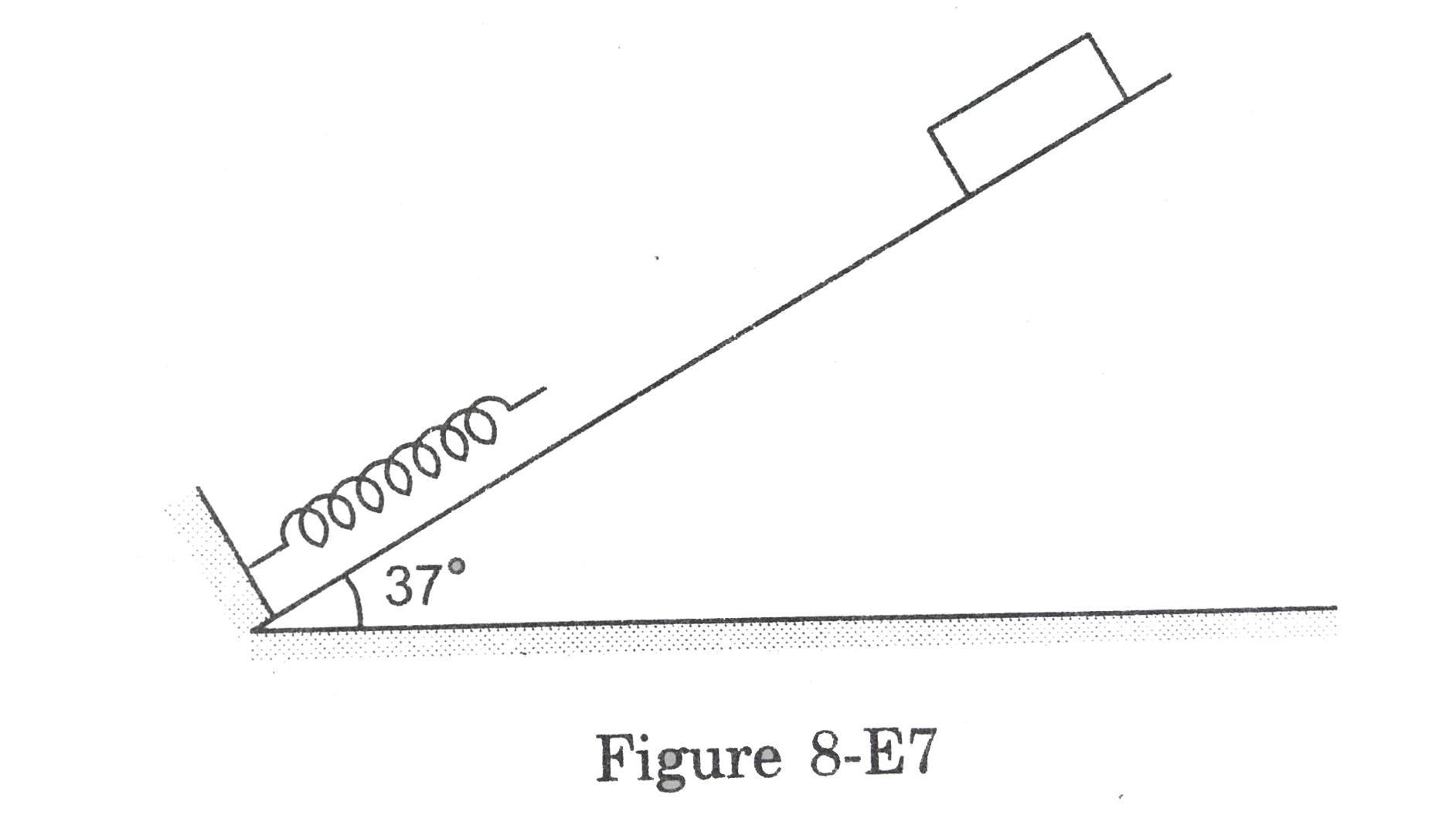
View SolutionFigure shows a spring fixed at the bottom end of an incline of inclination `37^0`. A small block of mass 2 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find a. the frictioin coefficient between the plane and the block and b. the spring constant of the spring. Take `g=10 m/s^2`.
View Solution(a) What is the power of an engine which can lift 600 kg of coal per minut from a mine 20 m deep ?
(b) A 2kW motor pumps out water from a well `10m` deep. Calculated the quantity of water pumped out per second.
View SolutionA truck can move up a road having a grade of 1.0 m rise for every 50 m with a speed of `18(km)//(h)`. The resisting force is equal to `(1)//(25)` of the weight of the truck. With what speed the same truck moves down the hill with the same power?
View SolutionAn engine is hauling a train of mass `m` on a level track at a constant speed `v`. The resistance due to friction is `f`. What power is the engine producing? What extra power must the engine develop to maintain the speed up a gradient 1 in l. What is the new total power developed by the engine develop to maintain the speed up a gradient 1 in l. What is the new total power developed by the engine ?
View SolutionIn generation of hydroelectric power, water falls from some height and gravitational potential energy of water is converted into electric power with the help of turbine. In one such event, `7.2xx10^4kg` of water falls per hour from height 100m and half of the gravitational potential energy is converted into electric energy. How much power is generated?
View SolutionA person decides to use bath tub water to generate electric power to run a 40 W bulb. The bath tub is located at a height of 10 m from the ground and it holds 200 liters of water. He installs a water driven wheel generator on the ground. At what rate should the water drain from the bath tub to light the bulb? The density of water is `1000(kg)//(m^3)` and efficiency of generator is `80%`. How long can he keep the bulb on if the bath tub was full initially.
View SolutionA block of mass 3 kg is pulled up on a smooth incline of angle `37^@` with the horizontal. If the block moves with an acceleration `2(m)//(s^2)`, find the power delivered by the pulling force at time 5 s after the motion starts. What is the average power delivered during the 5.0 s after the motion starts?
View SolutionA body of mass `m` is thrown at an angle `alpha` to the horizontal with the initial velocity `v_0` Find (a) instantaneous power of gravity as a function of time and
(b) mean power developed by gravity in time (i) `t=0` to `T`,
(ii) `t=0` to `(T)/(2)`, (iii) `t=(T)/(2)` to `t=T`, where `T` is the time of flight.
View SolutionAn automobile of mass m accelerates, starting from rest, while the engine supplies constant power P. Find its position and instantaneous velocity at time t assuming the automobile starts from rest.
View SolutionA small body of mass `m` is given velocity `v_0` at point `O` on rough horizontal surface. (a) Find the mean power developed by the friction force during the whole time of motion if the friction coefficient is constant and equal to `mu_0` (b) Find the maximum instantaneous power developed by the friction force, if the friction coefficient varies as `mu=mu_0x`, where `mu_0` is a constant and `x` is the distance from the point `O`.
View SolutionA particle located in a one-dimensional potential field has its potential energy function as `U(x)(a)/(x^4)-(b)/(x^2)`, where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionThe potential energy of a conservative force field is given by
`U=ax^(2)-bx`
where, a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.
View SolutionIf the potential energy function of a particle is given by `U=-(x^2+y^2+z^2)`J, whre x,y and z are in meters. Find the force acting on the particle at point `A(1m,3m,5m)`.
View Solution
EXAMPLES questions and complete solutions for chapter WORK, ENERGY AND POWER of CP SINGH PHYSICS (HINGLISH) of Class 11